[[443041]]

又一年又接近尾聲，還有三天我們就要告別 2021 年了。

各個 AI 領(lǐng)域也迎來了年度總結(jié)和未來展望，今天來講一講 AI 圈始終大熱的圖機器學習（Graph ML）。

2021 年，圖機器學習領(lǐng)域涌現(xiàn)出了成千上萬篇論文，還舉辦了大量的學術(shù)會議和研討會，出現(xiàn)了一些重大的進展。2022 年，圖機器學習領(lǐng)域又會在哪些方面發(fā)力呢

Mila 和麥吉爾大學博士后研究員、專注于知識圖譜和圖神經(jīng)網(wǎng)絡(luò)（GNN）研究的學者 Michael Galkin 在一篇博客中闡述了他的觀點。在文中，作者對圖機器學習展開了結(jié)構(gòu)化分析，并重點介紹了該領(lǐng)域的主要進展和熱門趨勢。作者希望本文可以成為圖機器學習領(lǐng)域研究者的很好的參考。

本圖由 ruDALL-E 生成。

作者主要從以下 12 個部分進行了詳細的梳理：

1. 圖 Transformers + 位置特征
2. 等變 GNNs
3. 分子的生成模型
4. GNNs + 組合優(yōu)化 & 算法
5. 子圖 GNN：超越 1-WL
6. 可擴展和深度 GNN：層數(shù) 100 及以上
7. 知識圖譜
8. 利用 GNN 做很酷的研究
9. 新的數(shù)據(jù)集、挑戰(zhàn)和任務(wù)
10. 課程和書籍
11. 庫和開源
12. 如何保持更新

圖 Transformers + 位置特征

GNN 在（通常是稀疏的）圖上運行，而 Graph Transformers (GT) 在全連接圖上運行，其中每個節(jié)點都連接到圖的其他節(jié)點。一方面，在節(jié)點數(shù)為 N 的圖中，圖的復(fù)雜度為 O(N^2) 。另一方面，GT 不會過度平滑，這是長程消息傳遞的常見問題。全連接圖意味著你有來自原始圖的真邊和從全連接變換添加的假邊，你需要進行區(qū)分。 更重要的是，你需要一種方法來為節(jié)點注入一些位置特征，否則 GT 不會超過 GNN。

今年最流行的兩個圖 transformer 模型為 SAN 和 Graphormer。Kreuzer、Beaini 等人提出的 SAN 采用拉普拉斯算子的 top-k 特征值和特征向量。 SAN 將光譜特征與輸入節(jié)點特征連接起來，在許多分子任務(wù)上優(yōu)于稀疏 GNN。

Ying 等人提出的 Graphormer 采用空間特征。首先，節(jié)點特征豐富了中心編碼；然后，注意力機制有兩個偏置項：節(jié)點 i 和節(jié)點 j 之間的最短路徑距離；依賴于一條可用最短路徑的邊緣特征編碼。

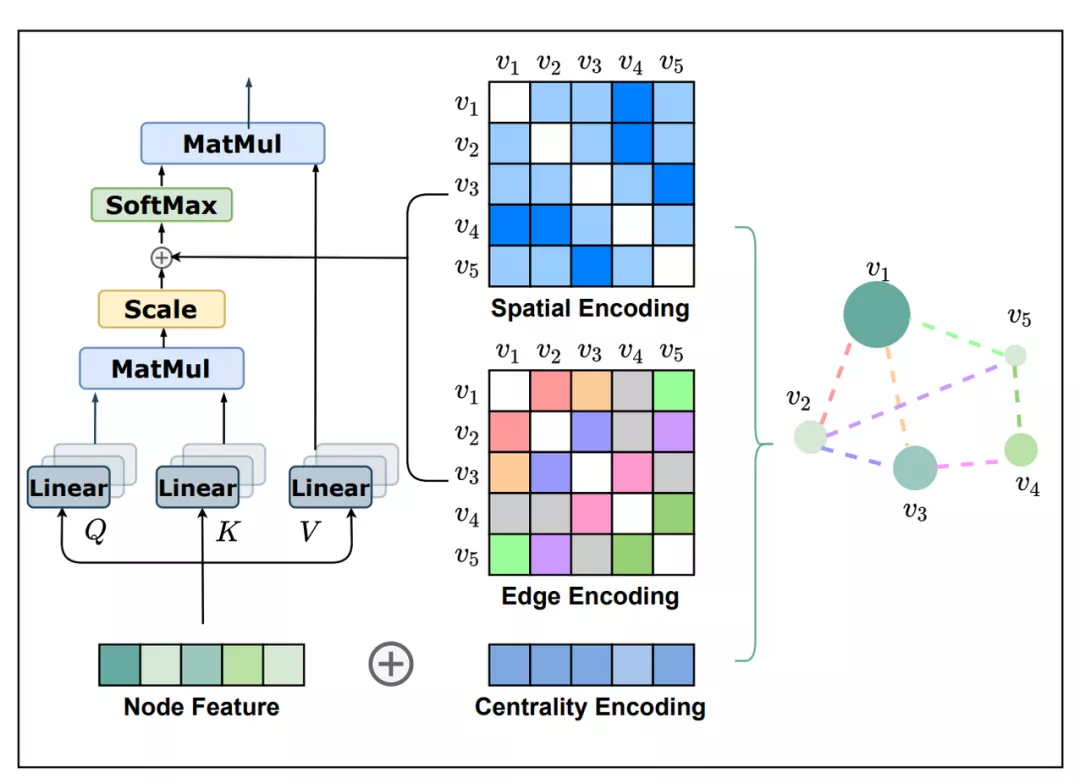
Graphormer 實現(xiàn)了 2021 年 Graph ML 大滿貫：OGB large Challenge 和 Open Catalyst Challenge 奪得冠軍

等變 GNN

等方差有何獨特之處，讓 Geoffrey Hinton 如此贊美？

一般來說，等方差被定義在某些轉(zhuǎn)換組上，例如，3D 旋轉(zhuǎn)形成 SO(3) 組，特殊正交以 3D 的形式組合。等變模型在 2021 年掀起了 ML 的風暴，在圖機器學習中的許多分子任務(wù)中尤其具有突破性。應(yīng)用于分子時，等變 GNN 需要一個額外的節(jié)點特征輸入，即分子物理坐標的一些表征，這些表征將在 n 維空間中旋轉(zhuǎn) / 反射 / 平移。

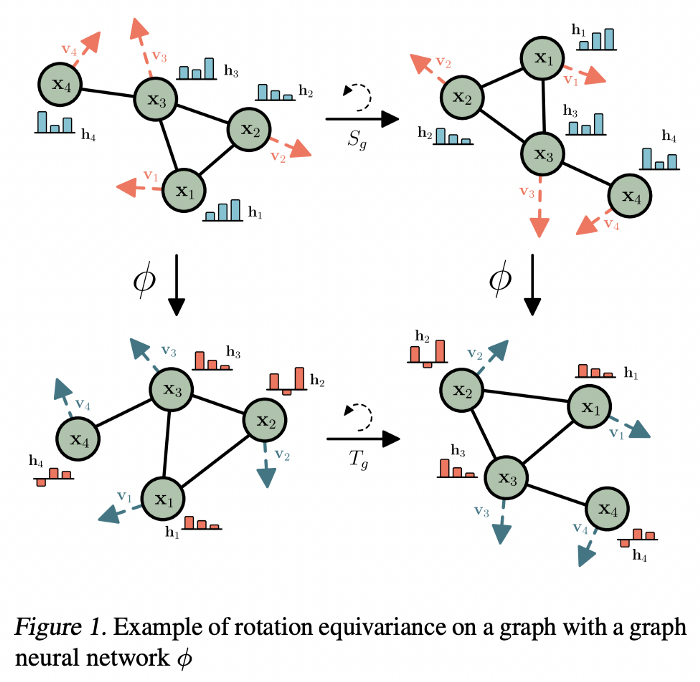
在等變模型中，盡管變換的順序不同，但我們都能到達相同的最終狀態(tài)。圖源：Satorras, Hoogeboom, and Welling

Satorras、Hoogeboom 和 Welling 提出了 EGNN、E(n) 等變 GNN，其與普通 GNN 的重要區(qū)別在于向消息傳遞和更新步驟添加物理坐標。 等式 3 將相對平方距離與消息 m 相加，等式 4 更新位置特征。 EGNN 在建模 n 體（n-body 系統(tǒng)、作為自動編碼器和量子化學任務(wù)（QM9 數(shù)據(jù)集）方面顯示出令人印象深刻的結(jié)果。

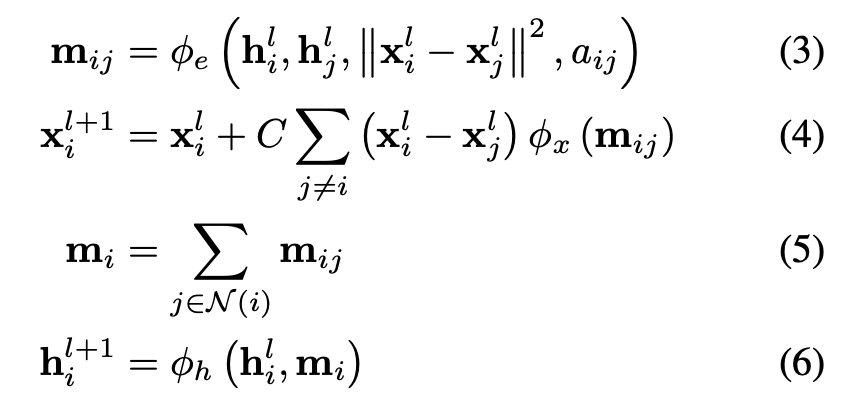
與 vanilla GNN 的主要區(qū)別：等式 3 和 4 將物理坐標添加到消息傳遞和更新步驟中。圖源：Satorras, Hoogeboom, and Welling

另一種選擇是合并原子之間的角度，就像 Klicpera、Becker 和 Günnemann 在 GemNet 中所做的那樣。 這可能需要將輸入圖轉(zhuǎn)換為折線圖，例如邊圖，其中來自原始圖的邊變成折線圖中的節(jié)點。 這樣，我們就可以將角度作為新圖中的邊緣特征。

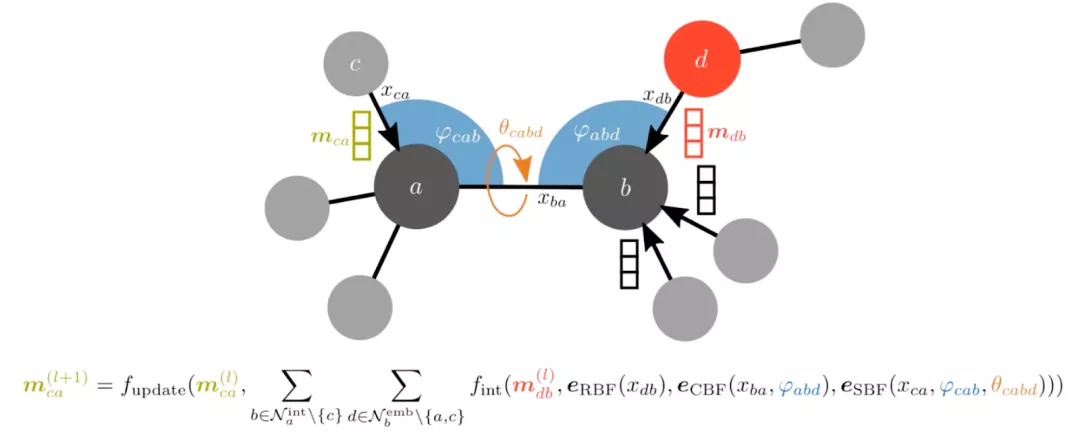
GemNet 在包括 COLL、MD17 和 Open Catalyst20 分子動力學任務(wù)上取得了不錯的成績， 顯然，等變 GNN 才剛剛起步，我們將在 2022 年看到更多進步！

分子的生成模型

由于幾何深度學習，整個藥物發(fā)現(xiàn) 領(lǐng)域在 2021 年實現(xiàn)了大幅的躍進。藥物發(fā)現(xiàn)的眾多關(guān)鍵挑戰(zhàn)之一是生成具有所需屬性的分子（圖）。這個領(lǐng)域很廣闊，這里只提到模型的三個分支。

歸一化流

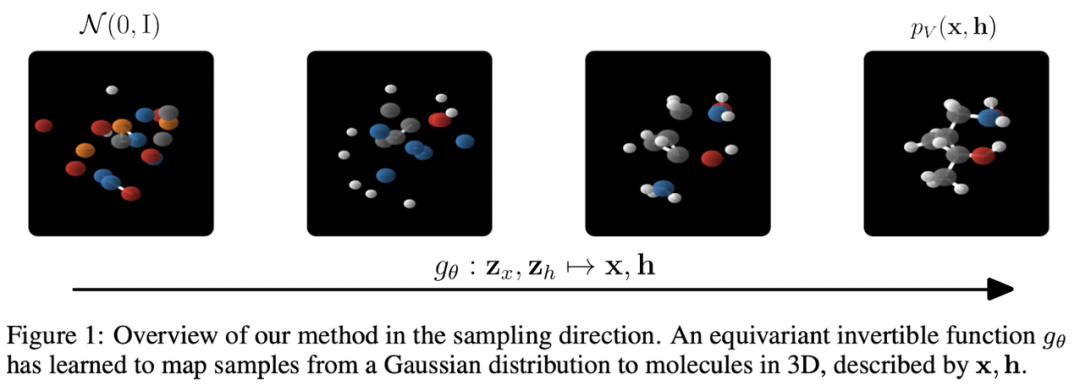
Satorras、Hoogeboom 等人應(yīng)用上述等變框架創(chuàng)建了 E(n) 等變歸一化流，能夠生成具有位置和特征的 3D 分子。

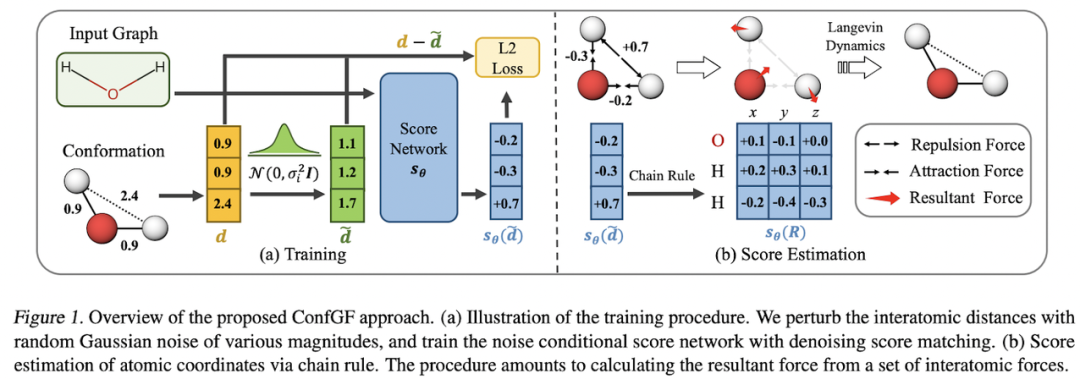
Shi、Luo 等人研究了在給定 2D 圖形的情況下生成 3D 構(gòu)象異構(gòu)體（即 3D 結(jié)構(gòu)）的問題。模型 ConfGF 估計了原子坐標對數(shù)密度的梯度場。這些字段是旋轉(zhuǎn)平移等變的，作者想出了一種方法將這種等變屬性合并到估計器中。Conformer 采樣本身是通過退火朗之萬動力學采樣完成的。

RL 方法

該方法是以一種非常非科學的方式描述的，這些方法通過逐步附加「構(gòu)建模塊」來生成分子。可以根據(jù)這些方法對構(gòu)建過程的調(diào)節(jié)方式對其進行廣義分類。

例如，Gao、Mercado 、 Coley 以可合成性為構(gòu)建過程的條件，即是否可以在實驗室中實際創(chuàng)建這種分子。為此，他們首先學習了如何創(chuàng)建構(gòu)建塊的合成樹（一種模板）。

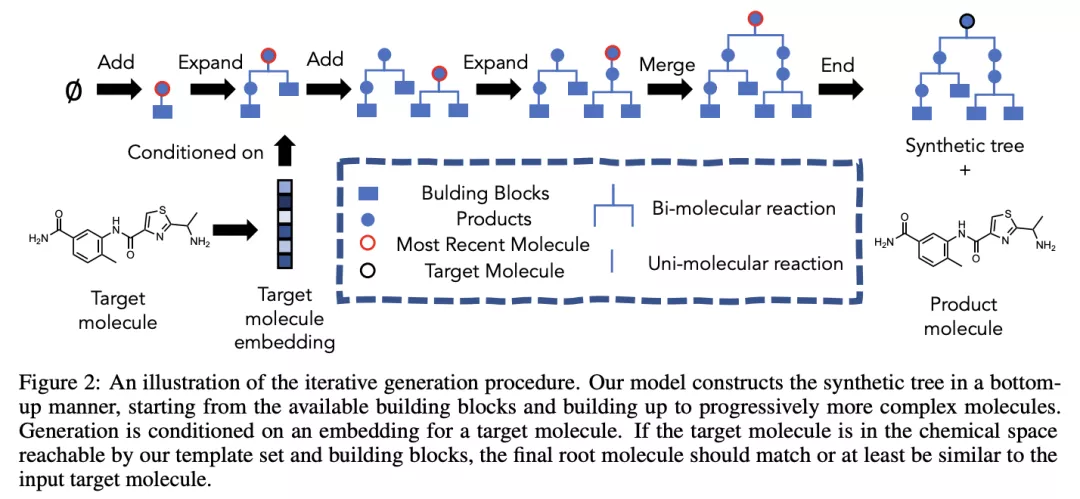
Yoshua Bengio 領(lǐng)導的 Mila 和斯坦福團隊提出了一個更通用的框架，他們引入了生成流網(wǎng)絡(luò)（GFlowNets）。這很難用幾句話來概括：首先，當我們想要對不同的候選者進行采樣時，GFlowNets 可以用于主動學習案例，并且采樣概率與獎勵函數(shù)成正比。此外，團隊最近的 NeurIPS'21 論文展示了 GFlowNets 應(yīng)用于分子生成任務(wù)的用處。Emmanuel Bengio 的博客文章更詳細地描述了該框架并提供了更多的實驗證據(jù)：http://folinoid.com/w/gflownet/

GNNs + 組合優(yōu)化 & 算法

2021 年，對于這個新興的子領(lǐng)域來說是重要的一年。

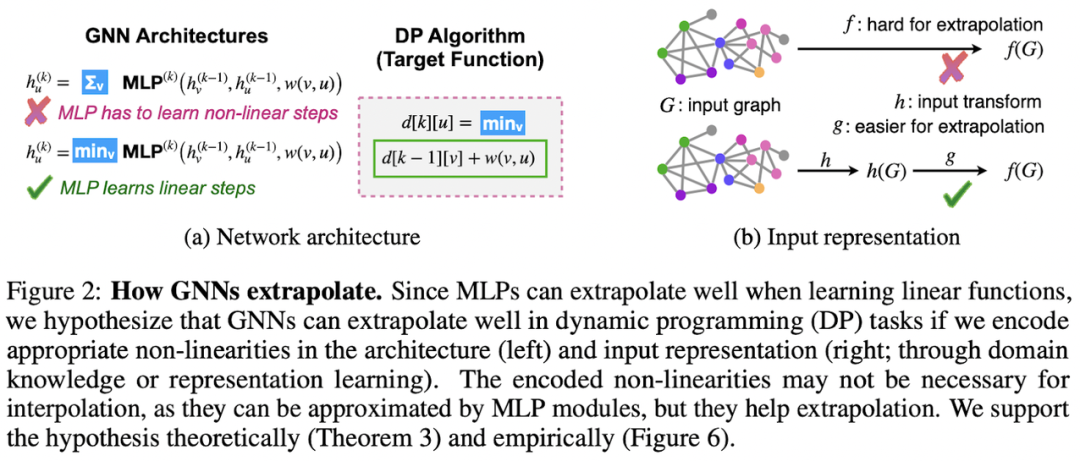
Xu et al 在 ICLR’21 的論文中研究了神經(jīng)網(wǎng)絡(luò)的外推，并得出了一些亮眼的結(jié)論。基于算法對齊的概念，作者表示，GNN 與動態(tài)規(guī)劃（DP）可以很好地對齊（如下圖所示）。事實上，將經(jīng)典 Bellman-Ford 算法尋找最短路徑的迭代和通過 GNN 的信息的聚合組合步驟做比較，會發(fā)現(xiàn)很多共同點。

此外，作者表明，在建模特定 DP 算法時，為 GNN 選擇合適的聚合函數(shù)至關(guān)重要，例如，對于 Bellman-Ford，需要一個最小聚合器（min-aggregator）。作者 Stefanie Jegelka 在 2021 年深度學習和組合優(yōu)化研討會上細致講述了這項工作的主要成果：https://www.youtube.com/watch?v=N67CAjI3Axw

為了更全面的介紹這個領(lǐng)域，還需要重點介紹 Cappart et al 在 IJCAI’21 上的一項研究，該調(diào)查涵蓋了 GNN 中的組合優(yōu)化。這篇文章首次出現(xiàn)了神經(jīng)算法推理藍圖，后來 Veličković 和 Blundell 的 Patterns 中的立場文件也對此進行了描述。

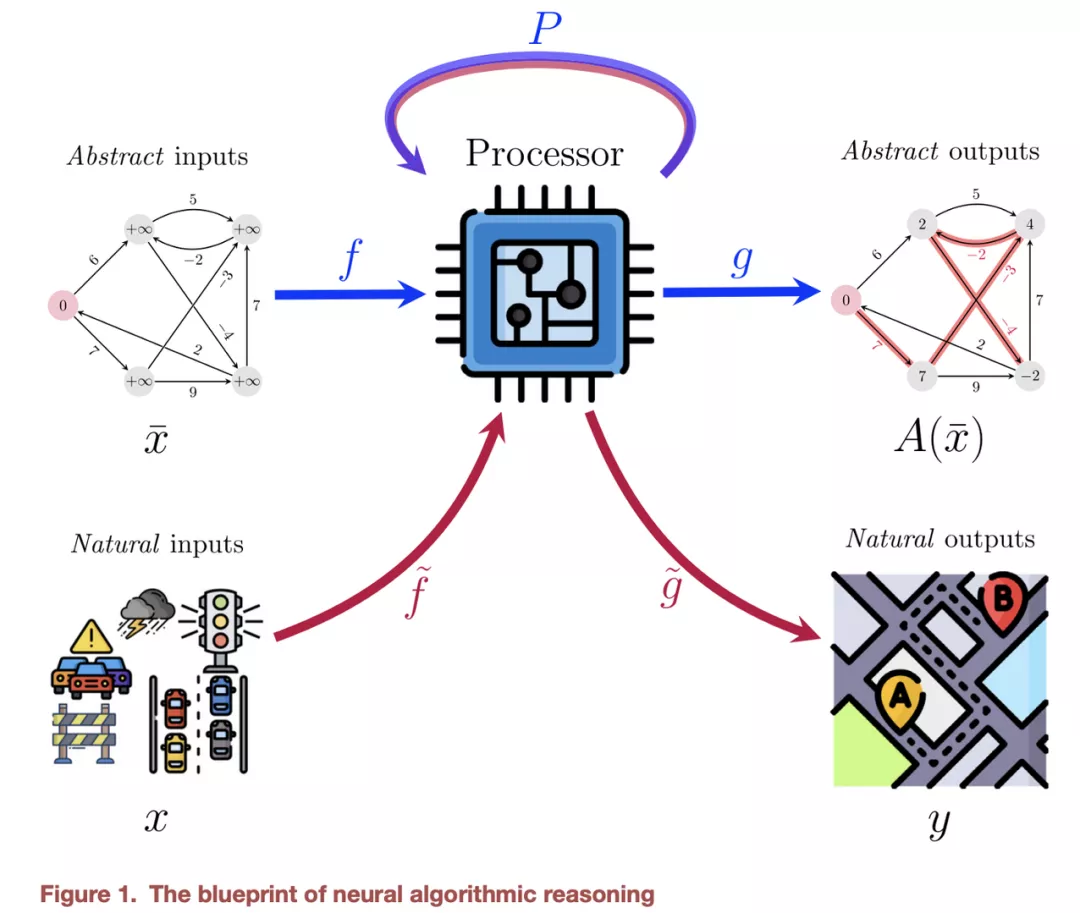
這個藍圖解釋了神經(jīng)網(wǎng)絡(luò)如何在嵌入空間中模仿和授權(quán)一般離散算法的執(zhí)行過程。在編碼 - 處理 - 解碼方式中，抽象輸入（從自然輸入獲得）由神經(jīng)網(wǎng)絡(luò)（處理器）進行處理，其輸出被解碼為抽象輸出，然后可以映射到更自然的任務(wù)特定輸出。

例如，如果抽象輸入和輸出可以表示為圖形，那么 GNN 可以即可成為處理器網(wǎng)絡(luò)。離散算法的一個常見的預(yù)處理步驟是將我們對這個問題的任何所知內(nèi)容轉(zhuǎn)化為像「距離」或「邊緣容量」這樣的標量，并在這些標量上運行算法。相反，向量表征和神經(jīng)執(zhí)行可以輕松啟用高維輸入而不是簡單的標量，并附加反向傳播以優(yōu)化處理器。

目前，該藍圖已經(jīng)得到越來越多的采用，NeurIPS'21 上出現(xiàn)了一些很酷的作品。Xhonneux et al 研究了遷移學習是否可用于將學習到的神經(jīng)執(zhí)行器泛化到新任務(wù)；Deac et al 發(fā)現(xiàn)了強化學習中算法推理和隱式規(guī)劃之間的聯(lián)系。相信在 2022 年還會出現(xiàn)更多有關(guān)研究。

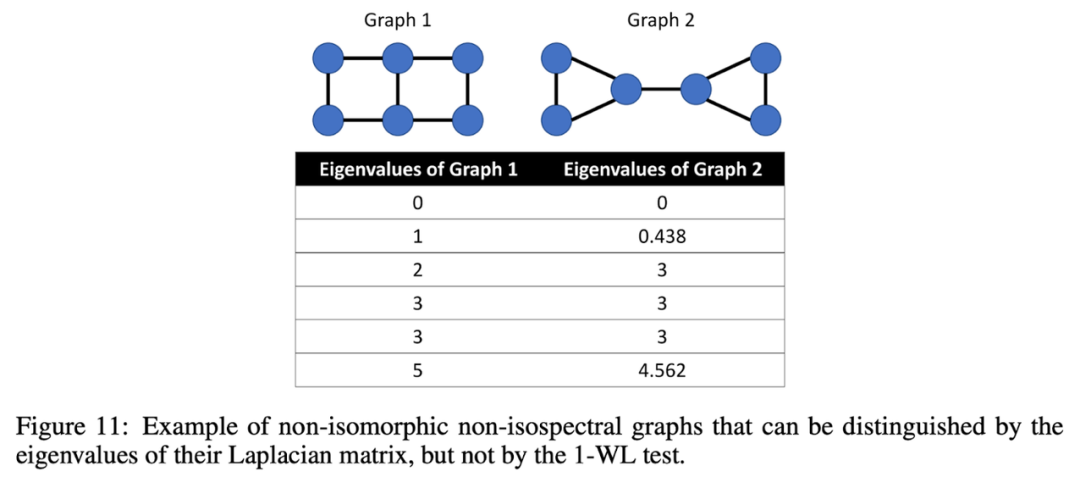
子圖 GNN：超越 1-WL

如果 2020 年是首次嘗試離開 GNN 表現(xiàn)力的 1-WL-landia 的一年，那么 2021 年則是超越 1WL-landia 的一年。這些聯(lián)系已被證明很有用，我們現(xiàn)在擁有一些強大且更具表現(xiàn)力的 GNN 架構(gòu)，這些架構(gòu)將消息傳遞擴展到更高階的結(jié)構(gòu)，如單純復(fù)形（例如 Bodnar、Frasca、Wang 等人的 MPSN 網(wǎng)絡(luò)、胞腔復(fù)形（Bodnar、Frasca 等人的 CW Networks ））或子圖。

可擴展性和深度 GNN

如果你在使用 2-4 層 GNN 時羨慕深度 ResNet 或 100 多層的大型 Transformer，那么 2021 年有兩篇論文為我們帶來了福音，一篇是關(guān)于隨意訓練 100-1000 層 GNN 的論文，另一篇是關(guān)于幾乎恒定大小的鄰域采樣。

Li 等人提出了兩種新機制，可以在訓練極深的超參數(shù)化網(wǎng)絡(luò)時減少 GPU 內(nèi)存消耗：將 L 層網(wǎng)絡(luò)的 O(L) 降低到 O(1)。作者展示了如何在 CV 或高效 Transformer 架構(gòu)（例如 Reformer）中使用可逆層，并在層之間共享權(quán)重（權(quán)重綁定），以訓練多達 1000 層的 GNN。下圖展示了根據(jù) GPU 需求進行的層數(shù)擴展。

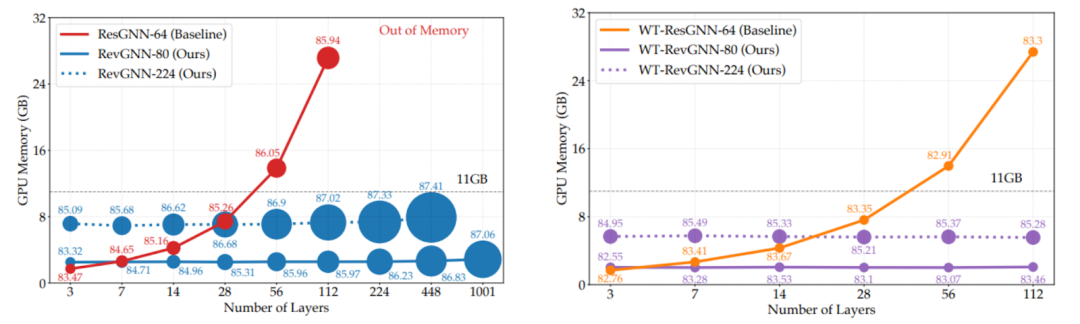
圖源：Li 等人的論文《 Training Graph Neural Networks with 1000 Layers 》

Godwin 等人提出了一種利用循環(huán)學習深度 GNN 的方法——在塊（Block）中組織消息傳遞步驟，每個塊可有 M 個消息傳遞層。然后循環(huán)應(yīng)用 N 個塊，這意味著有多個塊共享權(quán)重。如果有 10 個消息傳遞層和 10 個塊，你將得到一個 100 層的 GNN。其中一個重要的組成部分是 Noisy Nodes 正則化技術(shù)，它會干擾節(jié)點和邊的特征并計算額外的去噪損失。該架構(gòu)能更好地適用于分子任務(wù)，研究團隊還在 QM9 和 OpenCatalyst20 數(shù)據(jù)集上進行了評估。

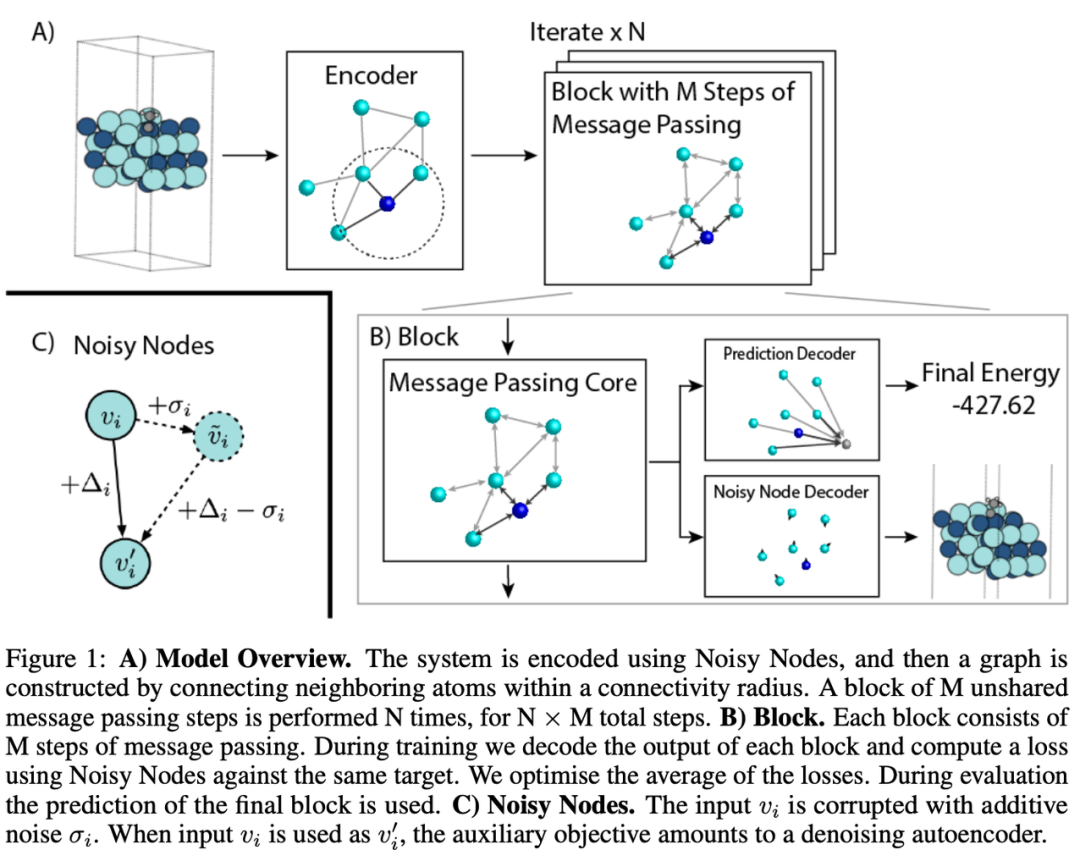
最后，如果想將任意 GNN 擴展成非常大的圖，那么只有一個選擇——采樣子圖。通常，對 k-hop 子圖進行采樣會導致指數(shù)級內(nèi)存成本和計算圖大小

PyG 的作者 Matthias Fey 等人創(chuàng)建了一個在恒定時間內(nèi)利用歷史嵌入和圖聚類擴展 GNN 的框架 GNNAutoScale。該方法在預(yù)處理期間將圖劃分為 B 個集群（小批量），以便最小化集群之間的連通性；然后在這些集群上運行消息傳遞與全批量設(shè)置一樣好，并顯著降低了內(nèi)存要求（小了約 50 倍），這使得在商品級 GPU 上安裝深度 GNN 和大型圖成為可能。

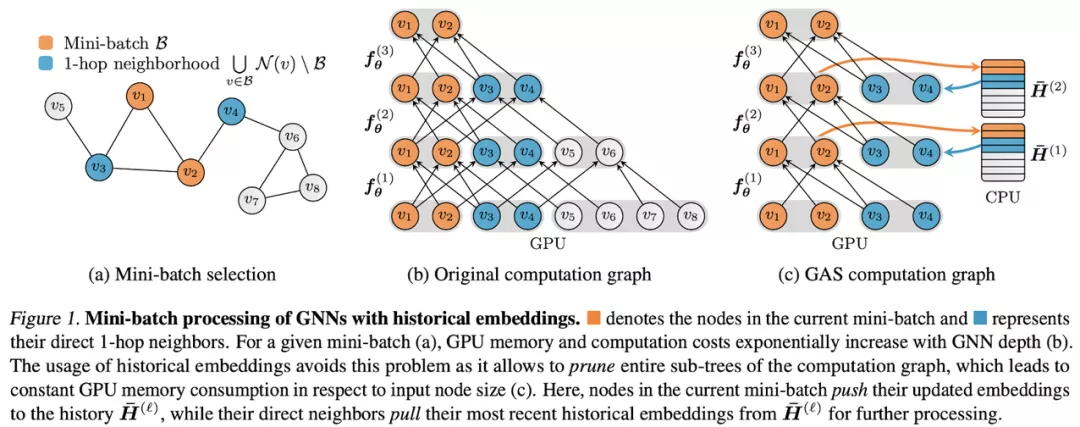
知識圖譜（KG）

在 2021 年之前，模型根據(jù)歸納偏置、架構(gòu)和訓練機制被明確分為轉(zhuǎn)導和歸納兩類。換句話說，轉(zhuǎn)導模型沒有機會適應(yīng)未見過的實體，而歸納模型在中大型圖上訓練成本太高。 2021 年有兩種新架構(gòu)在轉(zhuǎn)導和歸納環(huán)境中均可使用。這兩種架構(gòu)不需要節(jié)點特征，可以在歸納模式中以與轉(zhuǎn)導模式相同的方式進行訓練，并可擴展到現(xiàn)實世界的 KG 大小。

一種是 Zhu 等人的神經(jīng) Bellman-Ford 網(wǎng)絡(luò)，其中將經(jīng)典的 Bellman-Ford 推廣到了更高級別的框架，并展示了如何通過使用特定運算符實例化框架來獲得其他經(jīng)典方法（如 Katz 指標、PPR 、最寬路徑等）。更重要的是，該研究表明泛化的 Bellman-Ford 本質(zhì)上是一種關(guān)系 GNN 架構(gòu)。 NBFNet 不學習實體嵌入，這使得模型通過泛化到未見過的圖而獲得了歸納性。該模型在關(guān)系圖和非關(guān)系圖上的鏈接預(yù)測任務(wù)上都表現(xiàn)出色。在 KG 的應(yīng)用上，NBFNet 給 FB15k-237 和 WN18RR 兩個數(shù)據(jù)集帶來了自 2019 年以來最大的性能提升，同時參數(shù)減少了 100 倍。

另一種是 Galkin 等人受 NLP 中標記化算法啟發(fā)的新方法。在 KG 上應(yīng)用時，NodePiece 將每個節(jié)點表征為一組 top-k 個最近的錨節(jié)點和節(jié)點周圍的 m 個唯一關(guān)系類型。錨點和關(guān)系類型被編碼為可用于任何下游任務(wù)（分類、鏈接預(yù)測、關(guān)系預(yù)測等）和任何歸納 / 轉(zhuǎn)導設(shè)置的節(jié)點表征。 NodePiece 特征可以直接被 RotatE 等非參數(shù)解碼器使用，也可以發(fā)送到 GNN 進行消息傳遞。該模型在歸納鏈接預(yù)測數(shù)據(jù)集上的性能可與 NBFNet 媲美，并在大型圖上表現(xiàn)出較高的參數(shù)效率——OGB WikiKG 2 上的 NodePiece 模型所需參數(shù)僅為淺的僅轉(zhuǎn)導模型的一百分之一。

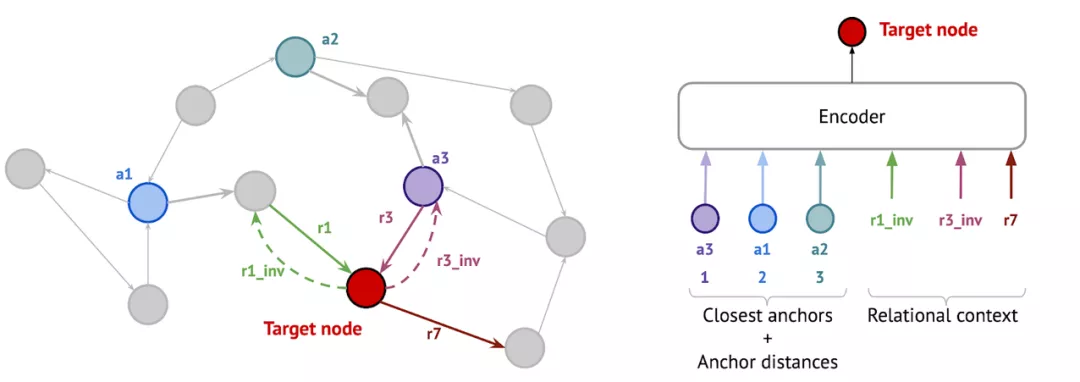
利用 GNN 做很酷的研究

Huang, He 等人在 ICLR’21 上展示了 Correct & Smooth — 一個通過標簽傳播改進模型預(yù)測的簡單程序。 僅與 MLP 配對，該方法在不使用任何 GNN 且參數(shù)少得多的情況下以最高分沖擊 OGB 排行榜！ 今天，幾乎所有 OGB 節(jié)點分類賽道中的頂級模型都使用 Correct & Smooth 來壓縮更多的點。

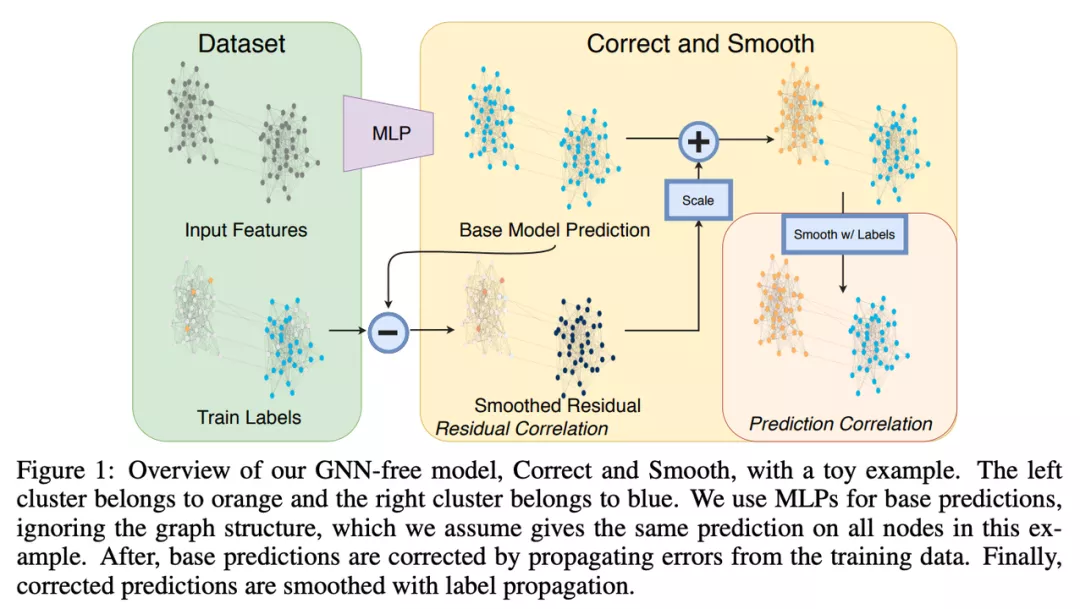
圖源： Huang, He 等人

Knyazev 等人在前向傳遞中預(yù)測各種神經(jīng)網(wǎng)絡(luò)架構(gòu)參數(shù)的工作震驚了 ML 社區(qū)。 他們沒有采用隨機初始化模型，而是采用預(yù)測好的參數(shù)，這樣會優(yōu)于隨機模型。

參數(shù)預(yù)測實際上是一個圖學習任務(wù)——任何神經(jīng)網(wǎng)絡(luò)架構(gòu)（ResNet、ViT、Transformers）都可以表示為一個計算圖，其中節(jié)點是具有可學習參數(shù)的模塊，節(jié)點特征是那些參數(shù)，網(wǎng)絡(luò)有 一堆節(jié)點類型（比如，線性層、卷積層等，作者使用了大約 15 種節(jié)點類型）。 參數(shù)預(yù)測則是一個節(jié)點回歸任務(wù)。 計算圖使用 GatedGNN 進行編碼，并將其新表示發(fā)送到解碼器模塊。 為了訓練，作者收集了一個包含 1M 個架構(gòu)（圖）的新數(shù)據(jù)集。 該方法適用于任何神經(jīng)網(wǎng)絡(luò)架構(gòu)，甚至適用于其他 GNN。

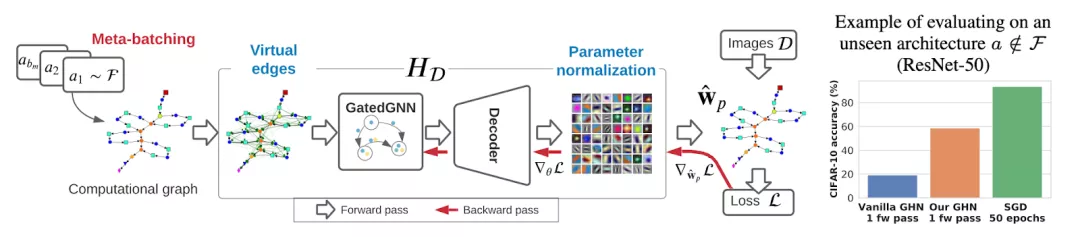
預(yù)測未知模型的參數(shù)的 pipeline。圖源：Knyazev 等人

DeepMind 和谷歌通過將道路網(wǎng)絡(luò)建模為超分段圖并在其上應(yīng)用 GNN，極大地提高了谷歌地圖中 ETA 的質(zhì)量。 在 Pinion 等人的論文中，該任務(wù)被定義為節(jié)點級和圖級回歸。 除此之外，作者還描述了許多需要解決的工程挑戰(zhàn)，以便在谷歌地圖規(guī)模上部署系統(tǒng)。 應(yīng)用 GNN 解決數(shù)百萬用戶面臨的實際問題。

論文地址：https://arxiv.org/pdf/2108.11482.pdf

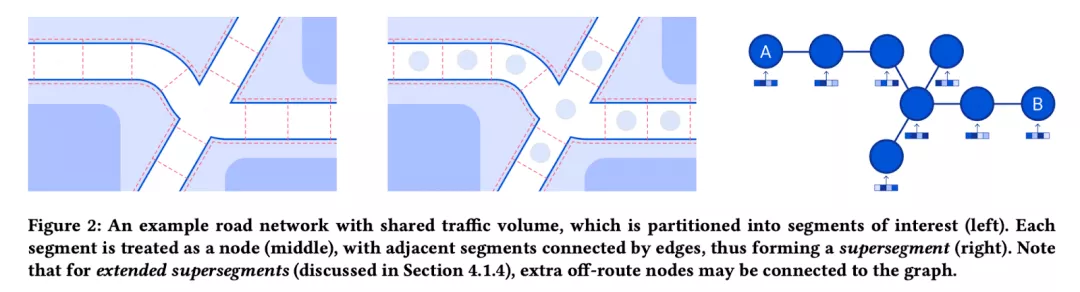
圖源: Pinion 等人

一些資料總結(jié)

文章最后，作者介紹了一些相關(guān)資料，包括數(shù)據(jù)集、課程和書籍、一些實用的庫等內(nèi)容。

如果你不習慣使用 Cora、Citeseer、Pubmed 數(shù)據(jù)集，可以考慮以下：

• OGB 數(shù)據(jù)集包含 3 個非常大的圖，可分別用于節(jié)點分類（240M 節(jié)點）、鏈接預(yù)測（整個 Wikidata，90M 節(jié)點）和圖回歸（4M 分子）任務(wù)。 在 KDD Cup 中，大多數(shù)獲勝團隊使用了 10-20 個模型組合；
• 由 Meta AI 發(fā)起的公開催化劑挑戰(zhàn)賽（ Open Catalyst NeurIPS’21 Challenge ），提供了一項大型分子任務(wù)——給出具有原子位置的初始結(jié)構(gòu)，預(yù)測其松弛狀態(tài)能。這個數(shù)據(jù)集非常龐大，需要大量的計算，但組織者暗示將發(fā)布一個更小的版本，這將對 GPU 預(yù)算有限的小型實驗室更友好。事實上，Graphormer 在 OGB LSC 和 OpenCatalyst ' 21 中都獲得了第一名，并在 2021 年獲得了 Graph ML 的大滿貫；
• GLB 2021 帶來了一組新的數(shù)據(jù)集，包括 Lim 等人提出的 non-homophilous graphs ，Tsitsulin 等人提出的 graph simulations，以及 Rozemberczki 等人提出的 spatiotemporal graphs 等；
• NeurIPS’21 數(shù)據(jù)和基準賽道帶來了新數(shù)據(jù)集，MalNet 可用于圖分類，該數(shù)據(jù)集的平均圖大小是 15k 節(jié)點以及 35k 邊；ATOM3D 可用于 3D 分子任務(wù)；RadGraph 可用于從放射學報告中提取信息。

由 Michael Bronstein、Joan Bruna、Taco Cohen 和 Petar Veličković 編寫的幾何深度學習原型書和課程，包含 12 個講座和實踐教程和研討會。

• 書籍地址：https://arxiv.org/pdf/2104.13478.pdf
• 課程地址：https://geometricdeeplearning.com/lectures/

此外，比較有價值的書籍和課程還包括

• 由 18 位學者參與撰寫的知識圖譜新書：https://kgbook.org/
• William Hamilton 的圖表示學習手冊：https://www.cs.mcgill.ca/~wlh/grl_book/

2021 年發(fā)布的庫包含 TensorFlow GNN 、TorchDrug。

• TensorFlow GNN 地址：https://github.com/tensorflow/gnn
• TorchDrug 地址：https://torchdrug.ai/

在 2021 年持續(xù)更新的庫包括：

• PyG 2.0 — 現(xiàn)在支持異構(gòu)圖、GraphGym 以及一系列改進和新模型；
• DGL 0.7 — 在 GPU 上進行圖采樣，更快的內(nèi)核，更多的模型；
• PyKEEN 1.6 — 更多的模型、數(shù)據(jù)集、指標和 NodePiece 支持；