神經網絡原來這么簡單,機器學習入門貼送給你 | 干貨
本文經AI新媒體量子位(公眾號ID:QbitAI)授權轉載,轉載請聯系出處。
你想學機器學習嗎?這里有一個入門貼適合你。
什么神經網絡、隨機森林、計算機視覺通通一網打盡。
這個Facebook軟件工程師做了一個入門貼。
專為基礎為零的初學者打造。
有基礎的同學,也可以來看看加深一下理解。

我們就以神經網絡為例先來一睹為快吧!
神經網絡概論
作者說,神經網絡并不復雜!
“神經網絡”一詞很流行,人們通常認為它很難,但其實要簡單得多。
是不是這樣呢?先看再說。
神經網絡的理解主要分為三個部分,神經元、神經網絡的構建、訓練神經網絡。
神經元——神經網絡的基本單元
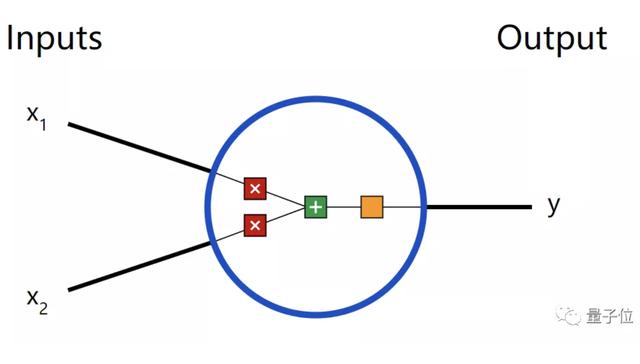
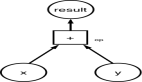
這是2-input神經元的樣子。
首先神經元接受輸入x1、x2,進行一些數學運算以后,然后產生一個輸出y。
在神經元里,通常會發生三件事:
1、每個輸入乘以相應的權重;
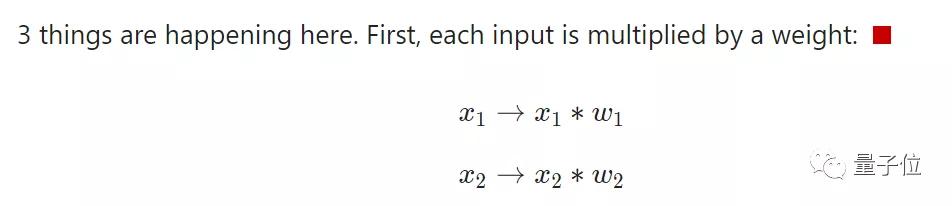
2、將所有加權輸入加在一起,在加上一個偏差b;
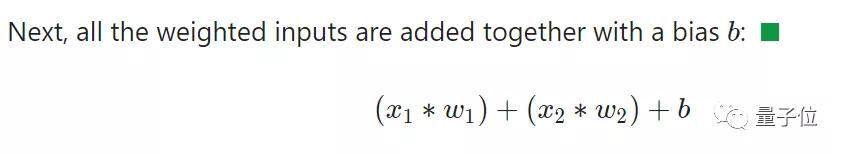
3、導入一個激活函數,得到輸出y。
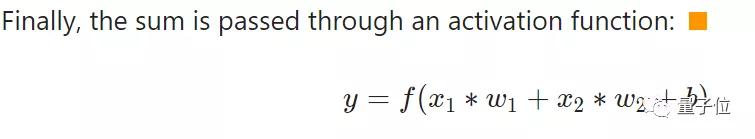
通常來說,激活函數使用Sigmoid函數,也就是常說的S型函數,輸入任意值(-∞,+∞),最后輸出都能停留在0-1之間。
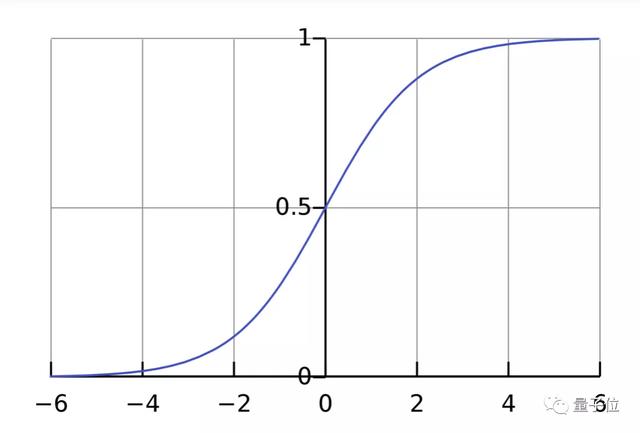
對此,他還舉了一個簡單的例子。
以激活函數是S型函數、2輸入神經元為例,設置參數 w=[0,1] (w1=0,w2=1),b=4。
input:x=[2,3]
output:y=0.999

這也就是最為樸素的神經網絡——前饋神經網絡。
對此,作者還用Python實現了整個過程。
- import numpy as np
- def sigmoid(x):
- # Our activation function: f(x) = 1 / (1 + e^(-x))
- return 1 / (1 + np.exp(-x))
- class Neuron:
- def __init__(self, weights, bias):
- self.weights = weights
- self.bias = bias
- def feedforward(self, inputs):
- # Weight inputs, add bias, then use the activation function
- total = np.dot(self.weights, inputs) + self.bias
- return sigmoid(total)
- weights = np.array([0, 1]) # w1 = 0, w2 = 1
- bias = 4 # b = 4
- n = Neuron(weights, bias)
- x = np.array([2, 3]) # x1 = 2, x2 = 3
- print(n.feedforward(x)) # 0.9990889488055994
構建神經網絡
神經元連接在一起就是神經網絡。
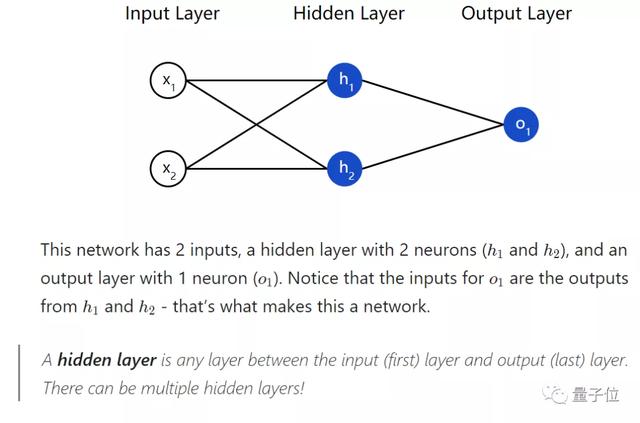
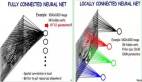
兩個輸入,一個含有兩個神經元的隱藏層,一個含有1個神經元的輸出層就構建了一個神經網絡。
需要注意的是,可以用多層隱藏層。就比如,像這樣:
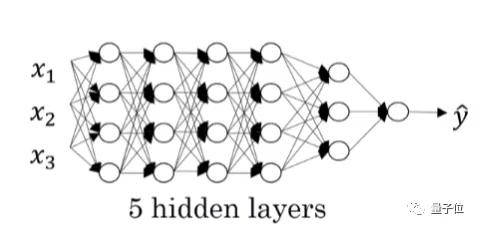
我們仍以上個示例的條件為例。

一個神經網絡可以包含任意數量的層和任意數量的神經元。
以Python代碼示例如下:
- import numpy as np
- # ... code from previous section here
- class OurNeuralNetwork:
- '''
- A neural network with:
- - 2 inputs
- - a hidden layer with 2 neurons (h1, h2)
- - an output layer with 1 neuron (o1)
- Each neuron has the same weights and bias:
- - w = [0, 1]
- - b = 0
- '''
- def __init__(self):
- weights = np.array([0, 1])
- bias = 0
- # The Neuron class here is from the previous section
- self.h1 = Neuron(weights, bias)
- self.h2 = Neuron(weights, bias)
- self.o1 = Neuron(weights, bias)
- def feedforward(self, x):
- out_h1 = self.h1.feedforward(x)
- out_h2 = self.h2.feedforward(x)
- # The inputs for o1 are the outputs from h1 and h2
- out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
- return out_o1
- network = OurNeuralNetwork()
- x = np.array([2, 3])
- print(network.feedforward(x)) # 0.7216325609518421
訓練神經網路——計算損失函數
假設,我們正在處理以下這個項目。通過人員的體重和身高來判斷性別。

以weight、height作為輸入,以gender作為輸出。
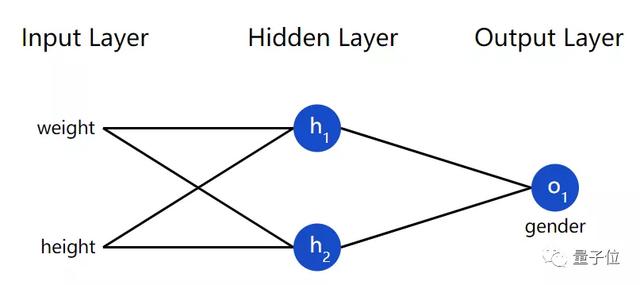
將Male設置為0,Female設置為1,還對其余數據進行了簡化。

在訓練神經網絡之前,首先需要一個方法來量化它做得有多“好”,是否能夠做得“更好”,那就是損失函數(loss)。
這里,我們將使用損失函數的一種——均方誤差來計算。

預測結果越好,說明損失也就會越低。而訓練神經網絡的目的,就在于盡可能的減少損失。
如果我們確信所有的人都是Male,也就是說預測值為0,會出現什么樣的結果?

Python示例:
- import numpy as np
- def mse_loss(y_true, y_pred):
- # y_true and y_pred are numpy arrays of the same length.
- return ((y_true - y_pred) ** 2).mean()
- y_true = np.array([1, 0, 0, 1])
- y_pred = np.array([0, 0, 0, 0])
- print(mse_loss(y_true, y_pred)) # 0.5
訓練神經網絡——最小化損失
計算了損失函數之后,就需要將損失最小化,這也是訓練神經網絡的最終目的所在。
接下來帖子有一段多變量演算,涉及微積分。
作者表示,
如果對微積分不滿意,可隨時跳過。
簡單起見,我們就假設這個數據集中只有Alice。
那么,它的損失函數就是這樣。

那么它的權重w跟偏差b,在圖上標示,那么就有6個權重變量,3個偏差變量。
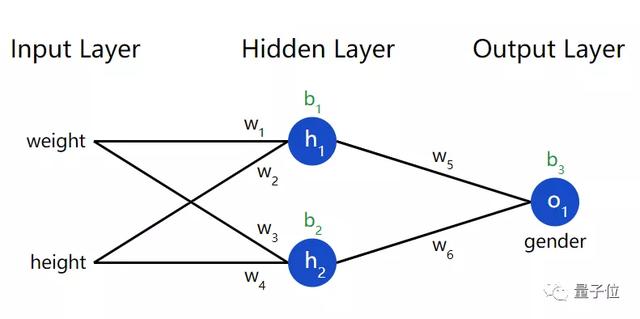
于是,便將損失函數寫為多變量函數。
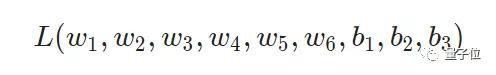
想象一下,我們只要調整w1,就可能導致L的變化。那具體是如何變化的呢?這就需要計算偏導數了。
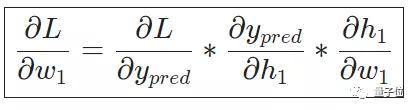
利用鏈式求導法則進行反向求導,而這一過程就叫做反向傳播。
詳細計算過程就不放在這里了,大家去他個人網站去看哦~(鏈接已附文末)
作者溫馨提示,看這個過程的時候不要著急,拿出手中的筆和紙,能夠幫助你理解。
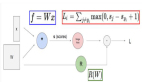
接下來,使用隨機梯度下降的優化算法,公式表示如下(以w1為例):

其中的“學習速率”控制著訓練速度,過大或者過小都不合適。
如果我們將所有的變量都進行這樣的優化,那么損失函數將逐漸減少,神經網絡就能夠得到改善。
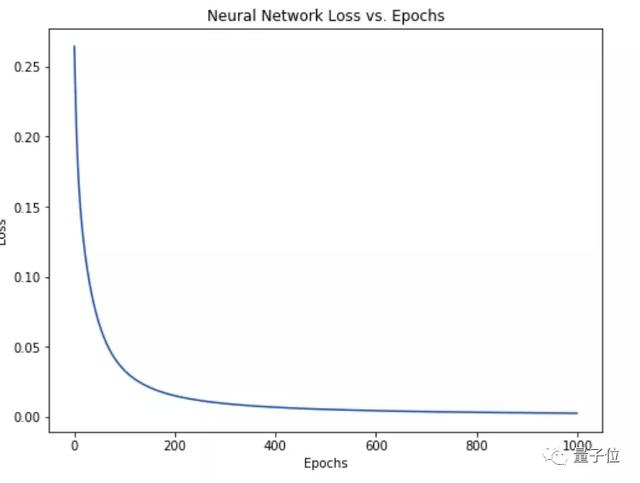
簡單來說,整個訓練過程是這樣的:
1、數據集中選擇一個樣本,就如Alice。
2、利用反向傳播計算所有變量的偏導數。
3、使用隨機梯度下降來訓練神經網絡,更新變量。
4、返回步驟1。
神經網絡的部分就介紹到這里,怎么樣?看完之后,有什么感想?
是不是覺得神經網絡也還好了。還有其他概念等著你來學習呢!