一、算法介紹

支持向量回歸（SVR）是一種監(jiān)督學(xué)習(xí)算法，用于解決回歸問題。其核心思想是找到一個(gè)超平面，這個(gè)超平面能夠以最小的誤差包含所有的訓(xùn)練樣本。與支持向量機(jī)處理分類問題類似，支持向量回歸的目標(biāo)是確保盡可能多的數(shù)據(jù)點(diǎn)位于由超平面決定的邊界內(nèi)。

二、算法原理

2.1 基本思想

SVR的目標(biāo)是找到一個(gè)函數(shù) ，使得該函數(shù)在整個(gè)數(shù)據(jù)集上的偏差最小，并且同時(shí)保證模型的復(fù)雜度較低，以提高模型的泛化能力。在實(shí)現(xiàn)上，這通常通過引入所謂的“軟間隔”來實(shí)現(xiàn)，允許某些數(shù)據(jù)點(diǎn)可以處于誤差允許的范圍之外，從而達(dá)到更好的預(yù)測效果。

2.2 數(shù)學(xué)模型

在支持向量回歸中，我們試圖找到一個(gè)線性函數(shù) ，其中 是權(quán)重向量， 是偏置。我們希望大部分的數(shù)據(jù)點(diǎn) 都滿足 ，這里的 是預(yù)先設(shè)定的一個(gè)小的非負(fù)數(shù)，表示容忍的誤差范圍。

為了找到這樣的函數(shù)，我們需要解決以下優(yōu)化問題：

其中， 和 是松弛變量，用于處理不在誤差范圍內(nèi)的數(shù)據(jù)點(diǎn)， 是正則化參數(shù)，用于控制模型復(fù)雜度和誤差之間的平衡。

2.3 核技巧

在實(shí)際應(yīng)用中，很多問題的數(shù)據(jù)分布可能是非線性的，直接使用線性函數(shù)進(jìn)行回歸可能無法達(dá)到較好的效果。SVR通過引入核函數(shù)來解決這一問題。核函數(shù)可以將數(shù)據(jù)映射到一個(gè)高維空間，在這個(gè)高維空間中，原本線性不可分的數(shù)據(jù)可能變得線性可分。常見的核函數(shù)包括線性核、多項(xiàng)式核、徑向基函數(shù)（RBF）核等。

三、案例分析

為了進(jìn)一步理解支持向量回歸（SVR）的應(yīng)用，我們將使用加州房價(jià)數(shù)據(jù)集進(jìn)行模型訓(xùn)練和測試。加州房價(jià)數(shù)據(jù)集包含以下特征：

• MedInc：收入中位數(shù)
• HouseAge：房屋年齡的中位數(shù)
• AveRooms：平均房間數(shù)目
• AveBedrms：平均臥室數(shù)目
• Population：區(qū)域人口
• AveOccup：平均入住率
• Latitude：緯度
• Longitude：經(jīng)度

數(shù)據(jù)集的目標(biāo)變量為MedHouseVal，即房屋價(jià)值的中位數(shù)（單位為$100,000）。

案例代碼

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

# 加載數(shù)據(jù)
california = fetch_california_housing()
X = pd.DataFrame(california.data, columns=california.feature_names)
y = california.target
X
# 數(shù)據(jù)預(yù)處理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 劃分訓(xùn)練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 創(chuàng)建SVR模型
svr = SVR(kernel='rbf')

# 訓(xùn)練模型
svr.fit(X_train, y_train)

# 預(yù)測測試集
y_pred = svr.predict(X_test)

# 計(jì)算MSE
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')

# 可視化實(shí)際值與預(yù)測值
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r--', lw=2)
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs. Predicted')
plt.show()

# 可視化誤差分布
errors = y_pred - y_test
plt.figure(figsize=(10, 6))
plt.hist(errors, bins=20, color='purple')
plt.xlabel('Prediction Error')
plt.ylabel('Frequency')
plt.title('Prediction Error Distribution')
plt.show()

四、結(jié)果分析

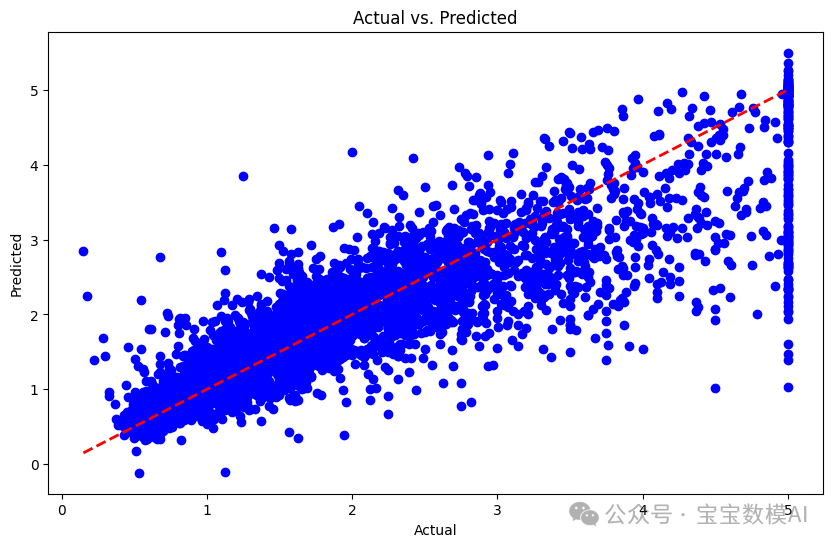
通過運(yùn)行代碼，得到模型在測試集上的平均平方誤差（MSE）為：0.3551984619989417。這個(gè)值越低，表示模型的預(yù)測能力越好。大家可以通過更換 SVR 的核函數(shù)類型（如 'linear', 'poly' 等）來嘗試改善模型的表現(xiàn)。

預(yù)測值與實(shí)際值的對比圖如下:

圖片

誤差分布圖如下：

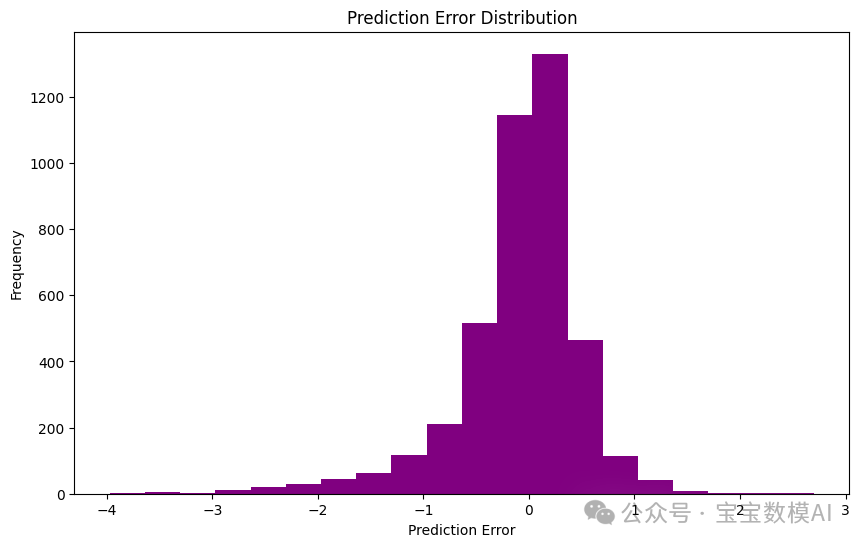圖片

五、結(jié)論

通過這個(gè)案例，我們可以看到支持向量回歸在實(shí)際數(shù)據(jù)集上的應(yīng)用。盡管 SVR 是一種強(qiáng)大的回歸工具，但選擇合適的核函數(shù)和調(diào)整模型參數(shù)對于獲得最佳性能至關(guān)重要。