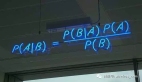在貝葉斯統(tǒng)計中,選擇合適的先驗分布是一個關鍵步驟。本文將詳細介紹三種主要的先驗分布選擇方法:

1. 經(jīng)驗貝葉斯方法
2. 信息先驗
3. 無信息/弱信息先驗

經(jīng)驗貝葉斯方法

經(jīng)驗貝葉斯方法是一種最大似然估計(MLE)方法,通過最大化先驗分布下數(shù)據(jù)的邊際似然來估計先驗分布的參數(shù)。設X表示數(shù)據(jù),θ表示參數(shù),則經(jīng)驗貝葉斯估計可表示為:

θ = argmax P(X|θ)

信息先驗

信息先驗是一種基于先前知識或以前研究結(jié)果,納入了關于估計參數(shù)信息或信念的先驗分布。信息先驗有以下幾個關鍵特點:

1. 在樣本量小或數(shù)據(jù)有噪聲的情況下,信息先驗可以導致更有效和準確的推斷。
2. 通過對先驗信息賦予更大的權重,信息先驗可以幫助正則化估計并避免過擬合。
3. 信息先驗有助于將特定領域的知識或假設納入模型,例如對參數(shù)值的約束或參數(shù)之間的關系。

以下是一些常見的信息先驗及其特點:

1. Beta先驗

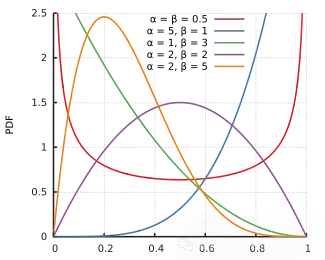
Beta先驗的概率密度函數(shù)(PDF)由下式給出:

• Beta分布通常用作二項式或伯努利模型中概率參數(shù)的先驗。
• 可以選擇參數(shù)α和β來反映關于概率的先驗知識或信念。例如,我們認為概率接近0.5,可以選擇α=β=1的Beta先驗,對應于[0,1]上的均勻分布。如果我們認為概率更可能接近0或1,可以選擇較大α和β值的Beta先驗,給極端值賦予更大的權重。
• 當我們對概率有一些先驗知識或信念,或者想要對概率的可能值施加約束時,首選Beta先驗。

2. 高斯先驗

• 高斯分布或正態(tài)分布是連續(xù)參數(shù)先驗的常見選擇。
• 先驗的均值和方差可以選擇反映關于參數(shù)的先驗知識或信念。例如,如果我們認為參數(shù)接近某個值,可以選擇均值等于該值且方差較小的高斯先驗。
• 當我們對參數(shù)的分布有一些先驗知識或信念,或者想要正則化估計并避免過擬合時,首選高斯先驗。

3. 狄利克雷先驗

• 狄利克雷分布通常用作多項式或分類模型中概率參數(shù)的先驗。
• 可以選擇參數(shù)αi來反映關于每個類別相對頻率的先驗知識或信念。例如,如果我們認為某些類別比其他類別更可能,可以為這些類別選擇較大αi值的狄利克雷先驗。
• 當我們對類別的相對頻率有一些先驗知識或信念,或者想要對概率的可能組合施加約束時,首選狄利克雷先驗。

4. 指數(shù)先驗

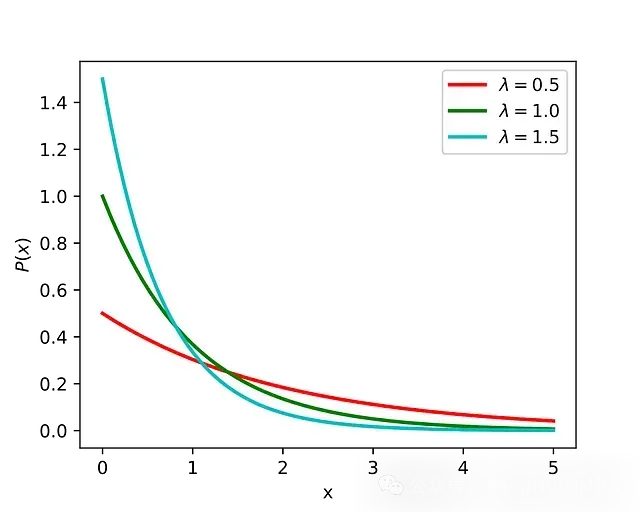
• 指數(shù)分布通常用作表示速率或時間參數(shù)的先驗。
• 可以選擇參數(shù)λ來反映關于速率或時間尺度的先驗知識或信念。例如,如果我們認為速率較低,可以選擇較大λ值的指數(shù)先驗。
• 當我們對速率或時間尺度有一些先驗知識或信念,或者想要正則化估計并避免過擬合時,首選指數(shù)先驗。

5. Gamma先驗

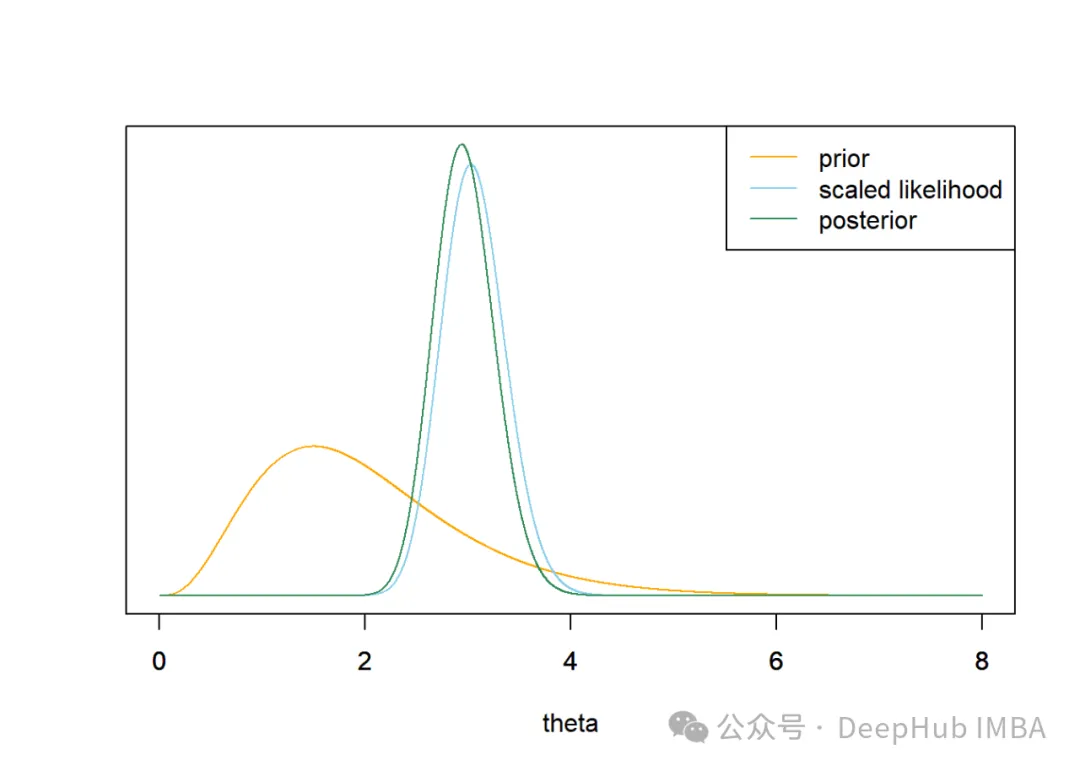
• Gamma分布是指數(shù)分布的推廣,可以用作表示速率或時間參數(shù)的先驗。
• 可以選擇參數(shù)α和β來反映關于速率或時間尺度的先驗知識或信念。
• 當我們對速率或時間尺度的分布有一些先驗知識或信念,或者想要正則化估計并避免過擬合時,首選Gamma先驗。

無信息/弱信息先驗

當我們對數(shù)據(jù)沒有先驗知識時,可以在貝葉斯統(tǒng)計中為方程的系數(shù)選擇無信息或弱信息先驗分布。無信息先驗不傳達關于參數(shù)值的任何強先驗信念或假設,而弱信息先驗傳達關于參數(shù)值的一些弱先驗信念或假設。

以下是一些可用于貝葉斯線性回歸模型中系數(shù)的無信息先驗:

無信息先驗

1. 平坦/均勻先驗

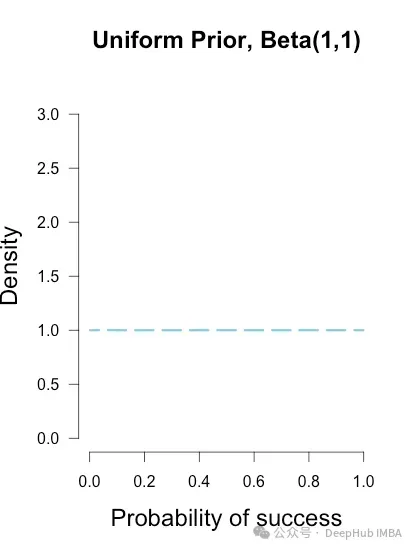
平坦/均勻先驗為參數(shù)的所有可能值分配相等的概率,例如在廣泛的值范圍內(nèi)的均勻分布。其概率密度函數(shù)為:

U(a, b), 其中a和b是分布的下限和上限。

2. 具有大方差的正態(tài)先驗

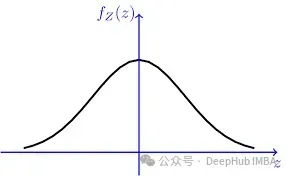
具有大方差的正態(tài)先驗假設參數(shù)在0附近正態(tài)分布,方差很大,表明我們對參數(shù)的先驗知識很少。例如,均值為0,方差為100的正態(tài)先驗,表示為:

N(0, σ2), 其中σ2是一個大值。

3. 柯西先驗

柯西先驗是一種重尾分布,為參數(shù)的所有可能值分配相等的概率,但與正態(tài)先驗相比,它在極端值上放置更多的概率質(zhì)量。當數(shù)據(jù)稀疏或包含異常值時,柯西先驗可能很有用。其概率密度函數(shù)為:

Cauchy(0, τ), 其中位置參數(shù)為0,比例參數(shù)為τ。

4. Jeffrey先驗

Jeffrey先驗是一種無信息先驗,與Fisher信息的平方根成正比,Fisher信息是數(shù)據(jù)中關于參數(shù)信息量的度量。該先驗在重新參數(shù)化下是不變的,并具有一些理想的數(shù)學性質(zhì)。由于Fisher信息完全由數(shù)據(jù)確定,不包含任何主觀或先驗關于數(shù)據(jù)的信念,因此Jeffrey先驗是無信息的。其概率密度函數(shù)為:

p(θ) ∝ √I(θ), 其中I(θ)是Fisher信息。

弱信息先驗

1. 小方差的正態(tài)先驗

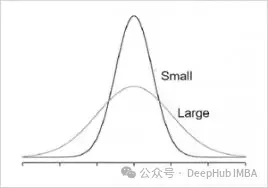
小方差的正態(tài)先驗假設參數(shù)在0附近正態(tài)分布,方差很小,表明我們對參數(shù)有一些弱先驗知識。例如,均值為0,方差為1的正態(tài)先驗,表示為:

N(0, σ2), 其中σ2是一個小值。

2. Student's t先驗

在樣本量小且總體標準差未知的情況下,可以使用Student's t先驗。它與正態(tài)先驗類似,但具有更重的尾部,允許更極端的值。當數(shù)據(jù)有噪聲或有異常值時,Student's t先驗可能很有用。其概率密度函數(shù)為:

t(0, σ, ν), 其中位置參數(shù)為0,比例參數(shù)為σ,自由度為ν。

3. 拉普拉斯先驗

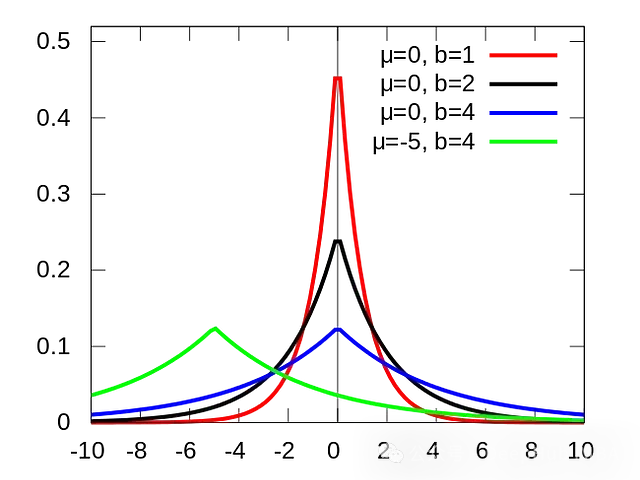
拉普拉斯先驗的概率密度函數(shù)與exp(-λ|θ|)成正比,其中λ是控制先驗強度的超參數(shù)。拉普拉斯先驗通過為接近0的θ值分配更多的概率質(zhì)量來鼓勵稀疏解。其概率密度函數(shù)為:

Laplace(0, λ), 其中位置參數(shù)為0,比例參數(shù)為λ。

值得注意的是,先驗的選擇取決于具體問題以及我們對參數(shù)擁有的先驗知識量。在實踐中,通常使用無信息先驗和弱信息先驗的組合,并評估結(jié)果對先驗選擇的敏感性。

總結(jié)

本文詳細介紹了貝葉斯統(tǒng)計中三種常見的先驗分布選擇方法:經(jīng)驗貝葉斯方法、信息先驗和無信息/弱信息先驗。

經(jīng)驗貝葉斯方法通過最大化先驗分布下數(shù)據(jù)的邊際似然來估計先驗分布的參數(shù)。信息先驗根據(jù)先前知識或研究結(jié)果,納入了關于估計參數(shù)的信息或信念。常見的信息先驗包括Beta先驗、高斯先驗、狄利克雷先驗、指數(shù)先驗和Gamma先驗。在樣本量小、數(shù)據(jù)有噪聲或需要納入領域知識時,信息先驗特別有用。

無信息先驗和弱信息先驗適用于缺乏先驗知識的情況。無信息先驗不傳達關于參數(shù)值的任何強先驗信念或假設,常見的無信息先驗包括平坦/均勻先驗、具有大方差的正態(tài)先驗、柯西先驗和Jeffrey先驗。弱信息先驗傳達關于參數(shù)值的一些弱先驗信念或假設,如小方差的正態(tài)先驗、Student's t先驗和拉普拉斯先驗。

在實踐中,先驗的選擇取決于具體問題和已有的先驗知識量。通常使用無信息先驗和弱信息先驗的組合,并評估結(jié)果對先驗選擇的敏感性。合理的先驗分布選擇可以提高貝葉斯推斷的效率和準確性,幫助我們更好地利用先驗知識和數(shù)據(jù),從而得到可靠的估計和預測結(jié)果。