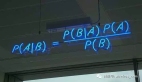貝葉斯推理三種方法:MCMC 、HMC和SBI
對許多人來說,貝葉斯統計仍然有些陌生。因為貝葉斯統計中會有一些主觀的先驗,在沒有測試數據的支持下了解他的理論還是有一些困難的。本文整理的是作者最近在普林斯頓的一個研討會上做的演講幻燈片,這樣可以闡明為什么貝葉斯方法不僅在邏輯上是合理的,而且使用起來也很簡單。這里將以三種不同的方式實現相同的推理問題。
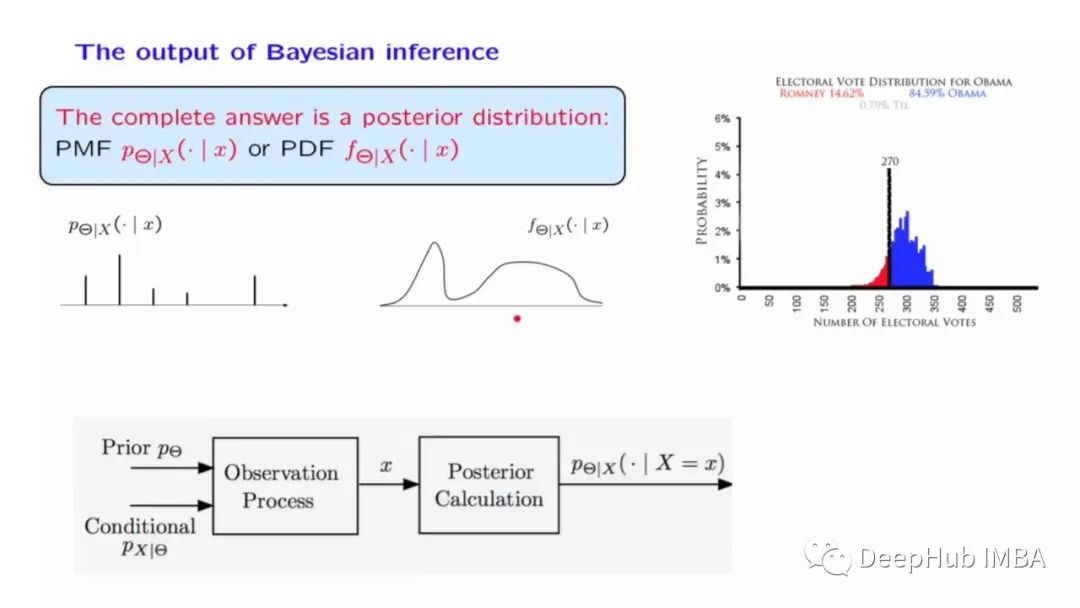
數據
我們的例子是在具有傾斜背景的噪聲數據中找到峰值的問題,這可能出現在粒子物理學和其他多分量事件過程中。
首先生成數據:
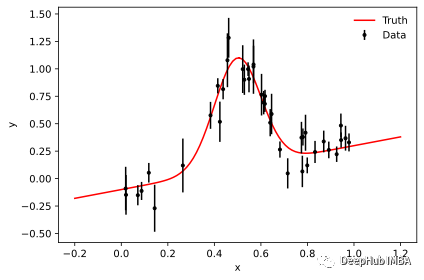
有了數據我們可以介紹三種方法了。
馬爾可夫鏈蒙特卡羅 Markov Chain Monte Carlo
emcee是用純python實現的,它只需要評估后驗的對數作為參數θ的函數。這里使用對數很有用,因為它使指數分布族的分析評估更容易,并且因為它更好地處理通常出現的非常小的數字。
結果如下:
我們應該始終檢查生成的鏈,確定burn-in period,并且需要人肉觀察平穩性:
現在我們需要細化鏈因為我們的樣本是相關的。這里有一個方法來計算每個參數的自相關,我們可以將所有的樣本結合起來:
emcee 的創建者 Dan Foreman-Mackey 還提供了這一有用的包corner來可視化樣本:
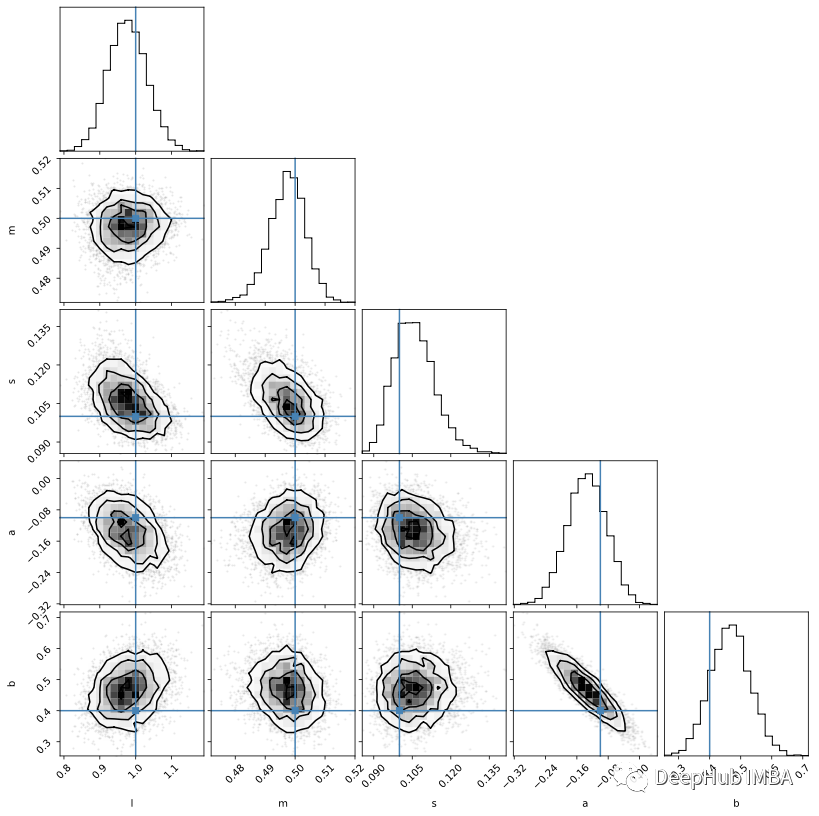
雖然后驗樣本是推理的主要依據,但參數輪廓本身卻很難解釋。但是使用樣本來生成新數據則要簡單得多,因為這個可視化我們對數據空間有更多的理解。以下是來自50個隨機樣本的模型評估:
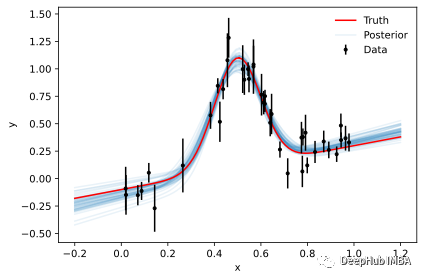
哈密爾頓蒙特卡洛 Hamiltonian Monte Carlo
梯度在高維設置中提供了更多指導。 為了實現一般推理,我們需要一個框架來計算任意概率模型的梯度。 這里關鍵的本部分是自動微分,我們需要的是可以跟蹤參數的各種操作路徑的計算框架。 為了簡單起見,我們使用的框架是 jax。因為一般情況下在 numpy 中實現的函數都可以在 jax 中的進行類比的替換,而jax可以自動計算函數的梯度。
另外還需要計算概率分布梯度的能力。有幾種概率編程語言中可以實現,這里我們選擇了 NumPyro。 讓我們看看如何進行自動推理:
還是使用corner可視化Numpyro的mcmc結構:
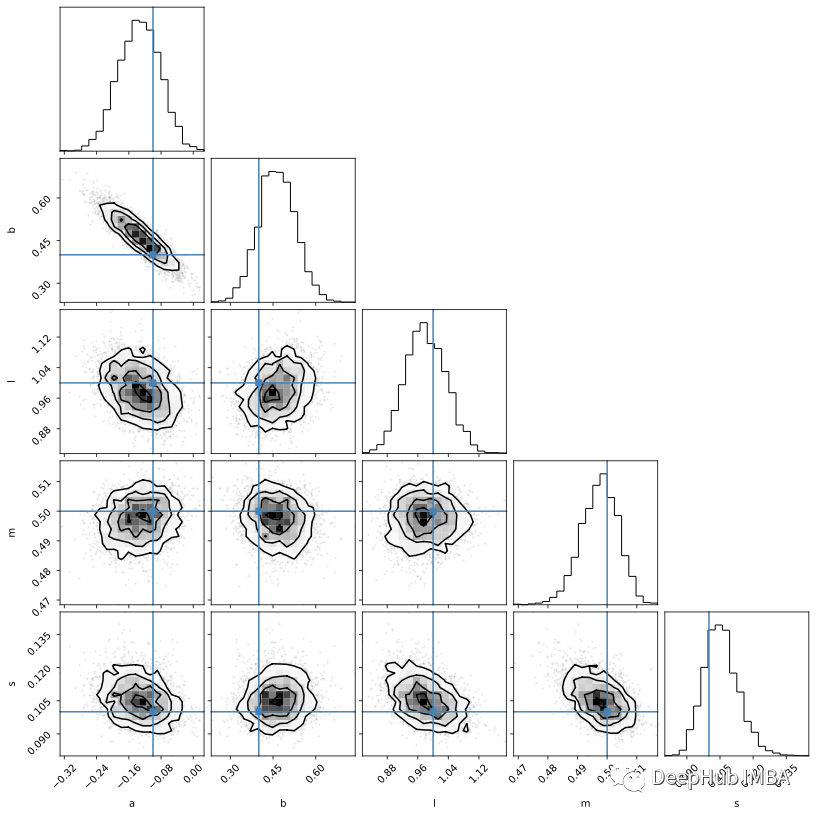
因為我們已經實現了整個概率模型(與emcee相反,我們只實現后驗),所以可以直接從樣本中創建后驗預測。下面,我們將噪聲設置為零,以得到純模型的無噪聲表示:
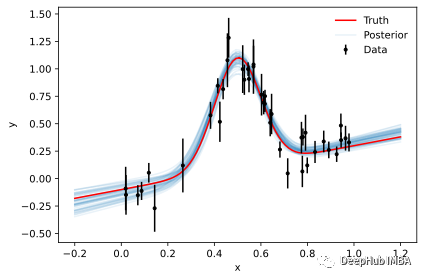
基于仿真的推理 Simulation-based Inference
在某些情況下,我們不能或不想計算可能性。 所以我們只能一個得到一個仿真器(即學習輸入之間的映射 θ 和仿真器的輸出 D),這個仿真器可以形成似然或后驗的近似替代。 與產生無噪聲模型的傳統模擬案例的一個重要區別是,需要在模擬中添加噪聲并且噪聲模型應盡可能與觀測噪聲匹配。 否則我們無法區分由于噪聲引起的數據變化和參數變化引起的數據變化。
讓我們來看看噪聲仿真器的輸出:
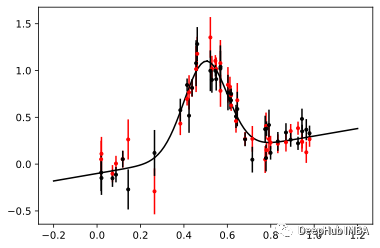
現在,我們使用 sbi 從這些模擬仿真中訓練神經后驗估計 (NPE)。
NPE使用條件歸一化流來學習如何在給定一些數據的情況下生成后驗分布:
在推理時,以實際數據 y 為條件簡單地評估這個神經后驗:
可以看到速度非常快幾乎不需要什么時間。
然后我們再次可視化后驗樣本:
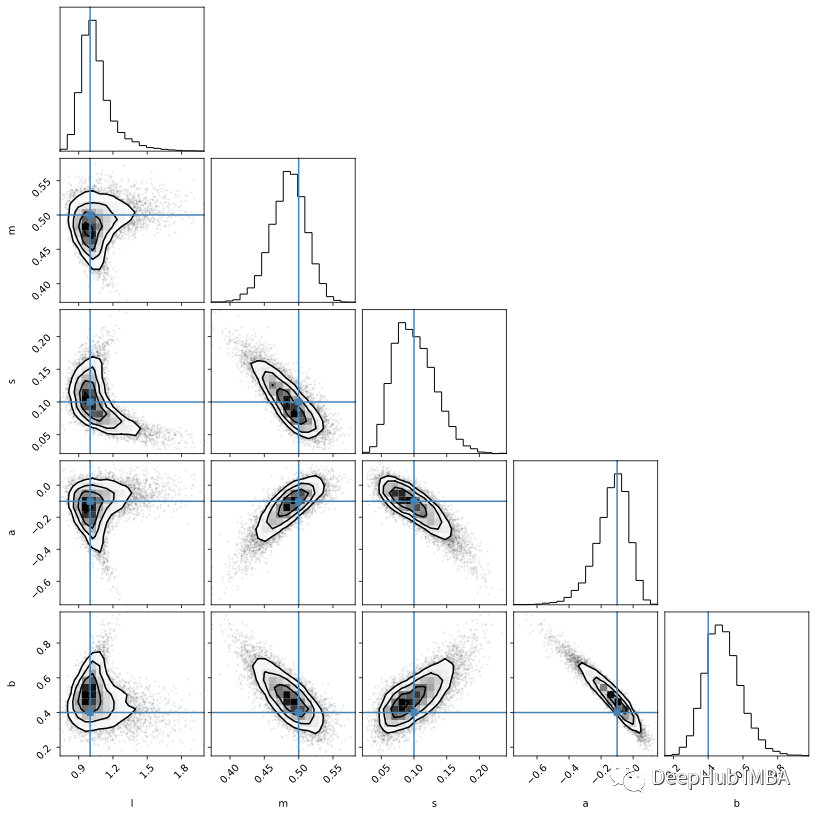
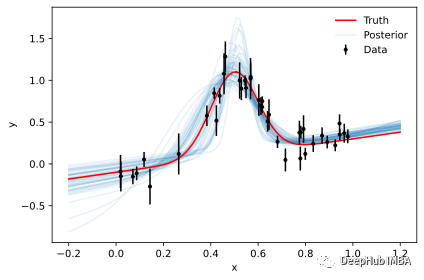
可以看到仿真SBI的的結果不如 MCMC 和 HMC 的結果。 但是它們可以通過對更多模擬進行訓練以及通過調整網絡的架構來改進(雖然并不確定改完后就會有提高)。
但是我們可以看到即使在沒有擬然性的情況下,SBI 也可以進行近似貝葉斯推理。