幾何學中，最難攻克的問題往往是一些最古老、最簡單的問題。

自古以來，藝術家和幾何學家們就想知道幾何形狀如何在沒有間隙或重疊的情況下鋪滿整個平面。然而用羅切斯特大學數學家 Alex Isoevich 的話來說——這個問題「直到最近才有所進展。」

?

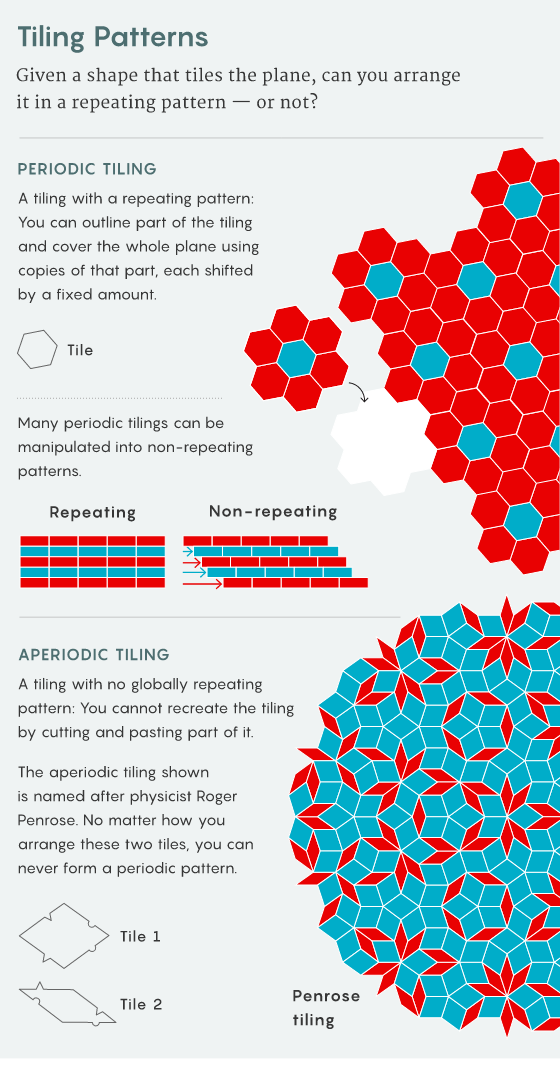
數學家想知道什么時候可以形成非周期性的平鋪模式——像彭羅斯平鋪這樣的模式，永遠不會重復。

最明顯的瓷磚重復模式是：用正方形、三角形或六邊形覆蓋地板很容易。不過在 1960 年代，數學家發現了一組奇怪的瓷磚，它們可以完全覆蓋平面，但只能以永不重復的方式覆蓋。

這就讓人不由地想要看看這種結構能有多瘋狂了。事實證明，確實瘋狂。

第一個這樣的非重復或非周期性圖案包含一組 20426 個不同的瓷磚。數學家想知道他們是否可以降低這個數字。到 20 世紀 70 年代中期，英國科學家羅杰 · 彭羅斯（他后來因使用數學方法證明黑洞是愛因斯坦廣義相對論的直接結果而獲得 2020 年諾貝爾物理學獎）證明了一組簡單的只有兩塊瓷磚（被稱為「風箏」和「飛鏢」）的配置就足夠了。

想鋪出不重復的形式并不難，你可以調整許多重復或周期性的平鋪以形成非重復的平鋪。比如考慮一個無限的正方形網格，像棋盤一樣對齊。

如果移動每一行，使其與其上方的行偏移不同的量，你將永遠無法找到可以像圖章一樣剪切和粘貼以重新創建完整平鋪的區域。真正的訣竅是像彭羅斯那樣，找到可以覆蓋整個平面的瓷磚組，但只能以不重復的方式覆蓋。

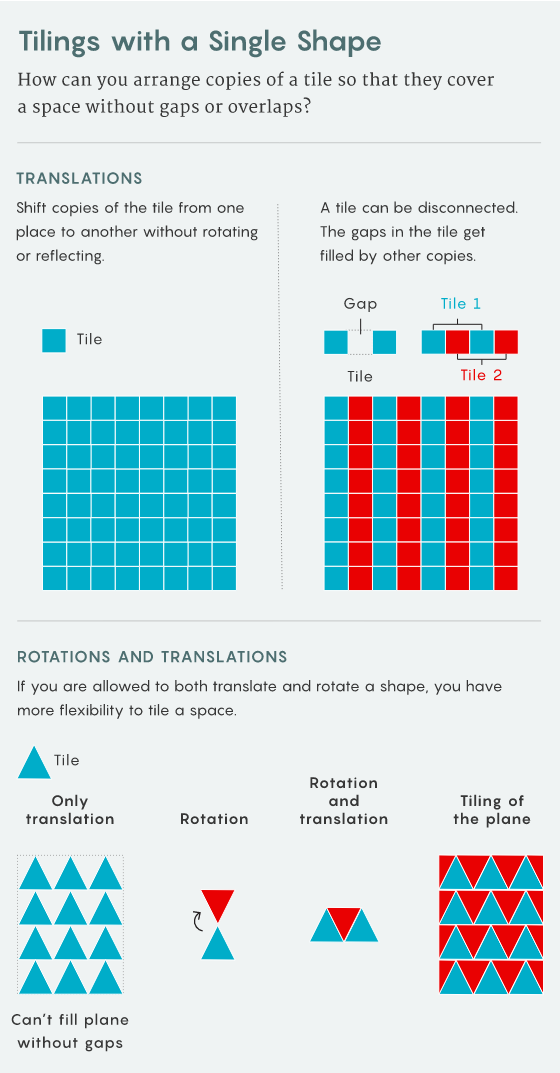
這就提出了一個問題：「可能有一塊形狀巧妙的瓷磚符合要求嗎？」

令人驚訝的是，答案是肯定的——如果允許移動、旋轉和鏡像瓷磚，就能找到一塊符合要求的瓷磚。如果瓷并沒有連接上，那么其中的間隙可以由其他適當旋轉、適當反射的瓷磚副本填充，最終覆蓋整個二維平面。

但是如果不允許旋轉這塊瓷磚，就不可能不留空隙地平鋪平面。

事實上，幾年前數學家 Siddhartha Bhattacharya 證明了——無論多么復雜或細化的瓷磚設計——如果只能使用單個瓷磚的移位或平移，那么就不可能設計出非周期性地覆蓋整個平面的瓷磚。

數學家 Bhattacharya 的二維猜想也適用于高維空間。這個假設被稱為周期性平鋪猜想，類似于不存在非周期性二維瓷磚一樣，數學家們也假設不存在合適的三維塊或更大維度的情況。

上個月，Greenfeld 和加州大學洛杉磯分校華人數學家陶哲軒（Terence Tao）最終解決了這個猜想——但不是以數學家預期的方式。他們構建了一個可以非周期性填充高維空間但不能周期性填充的「瓷磚」，從而推翻了這個猜想。

論文鏈接：https://arxiv.org/abs/2211.15847

克里特大學的數學家 Mihalis Kolountzakis 說：「我希望這個猜想在所有維度上都是正確的，但我想在足夠高的維度上，情況可能會不一樣。”

實際上，這個瓷磚問題不僅是個幾何問題，它還與幾何以外——邏輯本身極限的問題有關。

加州大學洛杉磯分校數學家 Rachel Greenfeld

合作研究

2019 年，Greenfeld 以博士后研究員的身份來到加州大學洛杉磯分校，她和陶哲軒兩人都獨立研究了與平移拼接相關的問題。兩位研究者也將目光投向了證明周期性平鋪猜想。

這個猜想在一維和二維中的結果已廣為人知，陶哲軒和 Greenfeld 試圖在三維的情況上證明它：證明如果你可以移動一個三維形狀來平鋪整個三維空間，那么一定有一種方法可以周期性平鋪空間。

他們取得了一些進展——使用不同的方法在二維中重新證明了這個猜想——他們希望新方法可以適用于三維情況。然而，他們碰壁了。 

陶哲軒說：「也許我們無法在更高維度上證明這個猜想是有原因的。我們應該開始尋找反例。」他們梳理了其他非周期性結構的文獻，然后著手尋找非周期性的反例。

他們從改變環境開始。假設平鋪一個二維空間，不要試圖平鋪一個連續的平面，考慮一個二維格子，一個排列在網格中的無限點陣列。你現在可以將圖塊定義為網格上的一組有限點，如果你有一個合適的平鋪，那么你可以通過復制有限的點集并將它們四處滑動來恰好覆蓋格子中的每個點一次。

證明高維格子的「離散」周期性拼接猜想與證明該猜想的連續版本略有不同，因為拼接在格子中是可能的，但在連續空間中是不可能的。但它們是相關的。Greenfeld 和陶哲軒想要提出一個離散的反例來證明他們隨后可以修改以在連續情況下也適用的猜想。

2021 年，他們在論文《Undecidable translational tilings with only two tiles, or one nonabelian tile》中接近了目標，在一個非常高維的空間中找到了兩塊瓷磚，其可以填充它們所在的空間，但只是無周期的。Greenfeld 說道。「非常接近了，但還不夠，但兩塊瓷磚比一塊更不牢固。」

又過了一年半時間，兩人為周期性平鋪猜想找到了一個真正的反例。

「瓷磚三明治」

他們從構建一種新語言開始，首先將問題重寫為一種特殊的方程式。這個方程式中的未知「變量」，即需要解決的問題代表了平鋪高維空間的所有可能方式。「但你很難用一個方程式來描述事物，」陶哲軒說。「有時你需要多個方程來描述一個非常復雜的空間集合。」

因此，Greenfeld 和陶哲軒重新構建了他們想要解決的問題。他們意識到可以轉而設計一個方程組，其中每個方程都會對其解編碼不同的約束。這讓他們可以將問題分解為一個關于許多不同瓷磚的問題——在其中，所有瓷磚都使用同一組翻轉覆蓋給定空間。

例如，在二維空間中你可以通過向上、向下、向左或向右滑動一個正方形來平鋪平面，一次一個單位。其他形狀也可以使用完全相同的一組偏移來平鋪平面：例如，一個正方形的右邊緣添加了一個凸起，左邊緣被移除，就像拼圖游戲一樣。

如果你把一個正方形、一塊拼圖和其他使用同一組移位的瓷磚，像三明治中的冷盤一樣把它們堆在一起，你就可以構建一個使用單一移位的瓷磚來覆蓋 3D 空間。Greenfeld 和陶哲軒需要的是在更多的維度上做這件事。

陶哲軒表示：「由于我們始終是在高維度上研究，多加一個維度并沒有真正妨礙到我們。」相反，這提供了額外的靈活性，以求得一個好的解決方案。

數學家們試圖扭轉這種夾層構建程序，將他們的單方程、高維平鋪問題改寫為一系列低維平鋪方程。這些方程后來決定了高維平鋪的構造是什么樣的。

陶哲軒說：「哪怕你只有兩塊瓷磚，它們也可以互相交談，做些復雜的事情。」

Greenfeld 和陶哲軒認為他們的平鋪方程系統是一個計算機程序。每一行代碼或方程都是一個命令，而命令的組合可以生成一個程序，實現一個特定的目標。「邏輯電路是由非常基本的對象構成的，AND 門和 OR 門等等，」陶哲軒說。「每一個都不是很有趣，但是你把它們堆在一起，就可以做出一個可以畫正弦波或在互聯網上通信的電路。」

「所以我們開始把我們的問題看作是一種編程問題，」他繼續說。他們的每一個命令都是一個不同的屬性，而最終瓷磚需要滿足這些屬性，所以作為一個整體的程序將保證任何符合所有標準的平鋪必須是非周期的。

那么問題來了，在所有這些平鋪方程中編碼什么樣的屬性，才能實現這一目標？例如，夾層中的一個瓷磚的形狀可能只允許某些類型的移動。數學家們必須小心翼翼地建立起約束清單，以避免限制到排除任何解決方案，但要足以限制到排除所有周期性解決方案。

Greenfeld 說：「這里的博弈是構建正確的約束水平，對正確的難題進行編碼。」

無限數獨

Greenfeld 和陶哲軒希望用他們平鋪方程編制的謎題是一個無限多行和大量而有限數量的列組成的網格。數學家們試圖用特定的數字序列填滿每一行和對角線，這些數字序列與他們可以用平鋪方程描述的約束類型相對應：他們將其比作一個巨大的數獨謎題。

然后，二人找到了非周期性的序列，意味著相關的平鋪方程系統的解決方案也是非周期性的。「這個謎題基本上只有一個解決方案，它是個有趣的東西，幾乎是但不完全是周期性的，」陶哲軒說。「我們花了很多時間才找到。」

「研究幾乎是周期性但不完全是周期性的函數，是數學中一直存在的東西，」不列顛哥倫比亞大學的數學家 Izabella ?aba 說。「但這次是一種非常不同的使用該類型結構的方式。」

正如 Iosevich 所說，Greenfeld 和陶哲軒創造了一個完全初級的對象，并將事情推到一個「看起來更復雜的情況」。

陶哲軒正在用兒童玩具探索瓷磚的配置，拍攝：Rachel Greenfeld。

在過程中，他們構建了一個高維的非周期平鋪，首先是在離散環境中，然后是在連續環境中。這種平鋪是如此復雜，充滿曲折和漏洞以至于幾乎無法覆蓋空間。「這是一個討厭的平鋪，」陶哲軒表示。「我們沒有試圖讓它變得漂亮。」

他和 Greenfeld 沒有計算它所處空間的維度，只知道它是巨大的，可能有 2 ^( 100^100) 那么大。「我們的證明是建設性的，所以一切都很明確，而且可以計算，」Greenfeld 說。「但因為它離最佳狀態非常非常遠，我們沒有檢查它。」

事實上，數學家們認為他們可以在更低的維度上找到非周期性平鋪。這是因為他們的構造中，一些技術性更強的部分涉及到在特殊空間中工作，這些空間在概念上「非常接近于 2D」。Greenfeld 不認為他們會找到一個 3D 的瓷磚，但她說一個 4D 的瓷磚是可行的。

因此，Iosevich 說，他們不僅僅是推翻了周期性平鋪的猜想。「他們以最顛覆的方式做到了這一點。」

不完備性的探索

這項工作標志著一種構建非周期性平鋪的新方法，Greenfeld 和陶哲軒認為這種方法可用于推翻其他與平鋪有關的猜想。反過來，這可能使數學家們進一步推動復雜性產生的邊界。

「似乎確實有一種新的原則，即高維幾何學就是討厭的，」陶哲軒表示。「但我們從 2D 和 3D 得到的直覺可能會產生誤導。」

這項工作不僅涉及人類直覺的邊界問題，還涉及數學推理的邊界問題。在 20 世紀 30 年代，數學家庫爾特 · 哥德爾（Kurt G?del）表明，任何足以發展基本算術的邏輯系統都是不完整的，即「哥德爾不完備定理」。在這個系統中，有些語句既不能被證明也不能被反駁。事實證明，數學中充滿了「不可判定」的語句。

同樣，這項工作也充滿了計算上不可判定的問題，任何算法都無法在有限的時間內解決的問題。數學家們在 20 世紀 60 年代發現，關于傾角的問題也可以是不可判定的。也就是說，對于某些形狀的集合，可以證明的是，在有限的時間內不可能弄清楚它們是否在給定的空間內鋪設瓷磚。(原則上，這樣做的唯一方法是考慮所有可能的方式，將瓷磚鋪在一起，直到時間終止）。

「這是一個非常簡單的問題，但還是超出了數學的范圍，」耶魯大學的數學家 Richard Kenyon 說。「這不是這種情況的第一個例子，即某種數學理論是不可判定的或不完整的，但它確實是最樸實的一個。」

去年，Greenfeld 和陶哲軒發現，一個關于高維瓷磚對的一般定理是不可判定的。他們證明，沒有人能夠弄清楚某些成對的瓷磚是否能夠完全覆蓋它們所在的空間（無論是周期性的還是非周期性的）。

關于單個瓷磚的定理是否也是不可判定的？自 20 世紀 60 年代以來，人們知道，如果周期性平鋪猜想是真的，那么總是有可能確定任何給定的瓷磚是否可以覆蓋平面。

但相反的情況不一定是真的。僅僅因為一個非周期性平鋪存在，這并不意味著一個不可判定的平鋪也存在。

這就是 Greenfeld 和陶哲軒接下來想要弄清楚的事情——如何應用他們為這項成果所開發的一些技術。陶哲軒說：「我們創造的語言應該能夠創造出一個不可判定的謎題，這是非常合理的。因此，可能對于一些瓷磚，我們將永遠無法證明它是平鋪空間還是非平鋪空間。」

為了證明一個語句是不可判定的，數學家通常表明它等同于另一個已經知道是不可判定的問題。因此，如果這個平鋪問題被證明也是不可判定的，它就可以作為證明其他背景下的不可判定性的又一個工具，這些背景遠遠超出了關于如何平鋪空間的問題。

同時，Greenfeld 和陶哲軒的這項工作也是一種警示。Iosevich 說：「數學家們喜歡漂亮、干凈的定理。但你不要相信聽到的一切。不幸的是，數學中所有有趣的語句未必都是漂亮的，而且它們不一定按照我們希望的方式運行。」