「陶哲軒×GPT-4」合寫數學論文!數學大佬齊驚呼,LLM推理神助證明不等式定理
今年6月,陶哲軒曾在博客中預言,2026年,AI將與搜索和符號數學工具相結合,成為數學研究中值得信賴的合著者。
這個預言,如今已經愈發成真。
就在6月底,加州理工、英偉達、MIT等機構的學者,曾構建了一個基于開源LLM的定理證明器。
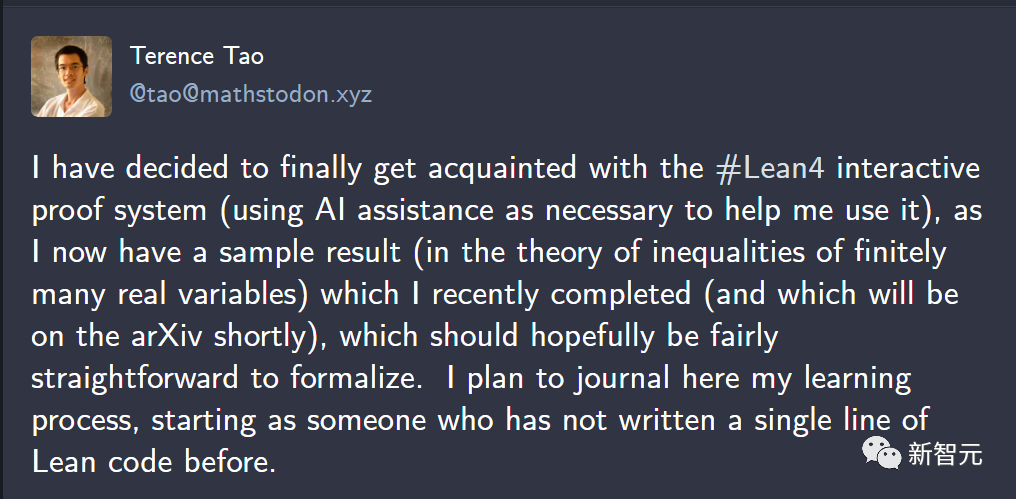
最近,陶哲軒又發現,在使用Lean進行自然數游戲研究時,GPT-4竟然也起到一些作用。
在AI的輔助下,他得到了關于有限多個實變量不等式理論的成果,論文很快就會發在arXiv上。
 圖片
圖片
如何用GPT-4研究自然數游戲
什么是自然數游戲?
 圖片
圖片
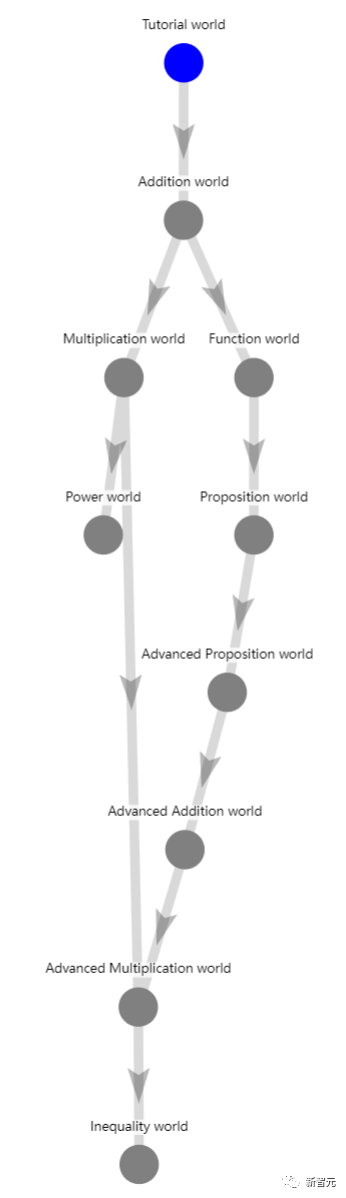
這個游戲,神奇地展示了歸納的力量。
如圖所示,我們從藍色節點上輸入,而灰色節點上方的所有結點都完成時,灰色節點將變為藍色。
在這個過程中,我們當然可以隨時嘗試任何級別的節點,但如果它是灰色的,我們可能就沒有足夠的知識來完成這個節點。
 引理:對于所有自然數x、y和z都有xy+z=xy+z。證明開始!
引理:對于所有自然數x、y和z都有xy+z=xy+z。證明開始!
在自然數游戲中,我們就會在定理證明器Lean中,得到自己的一個自然數版本——mynat。這個自然數滿足了數學歸納定理,以及其他原理(比如皮亞諾公理)。
 圖片
圖片
不過,問題在于,目前還沒有人證明這些關于自然數的定理,比如,你可以定義加法,但還沒有人證明x + y = y + x。
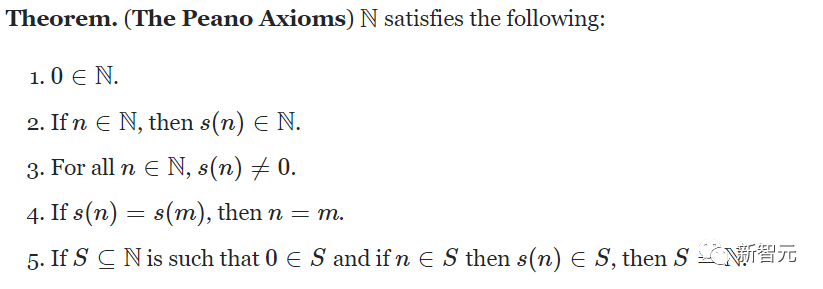 皮亞諾公理
皮亞諾公理
而自然數游戲,就需要你解決游戲中的關卡,用Lean定理證明器來證明數學定理。

我們證明了n+0=n,這個證明被稱為add_zero。但并不能證明zero_add,0+n=n。這兩個定理不是一樣嗎?并非如此!事實上x + y = y + x,這是加法世界的BOSS級難題。
陶哲軒是出于怎樣的機緣巧合,開始玩自然數游戲的呢?
原來,他是在IPAM機器輔助證明研討會上看到過幾次Lean的演示,并且被建議玩一玩自然數游戲,來熟悉Lean中用于證明定理的基本語法和策略。
讓陶哲軒感到驚喜的是,這個游戲越玩越熟悉,因為它證明的結果和自己寫的本科實分教材前幾章的結果分成相似。
 圖片
圖片
比如,從皮亞諾公理建立基本的算術事實,例如乘法的交換性和結合性。
另外,自然數游戲還讓他想起了自己編碼的邏輯游戲。
才玩了三個小時,陶哲軒就已經到達了「高級乘法」世界。他表示,在以后的空閑時間里他會繼續玩這個游戲。
 圖片
圖片
高級乘法世界:證明兩個非零自然數的乘積為非零:a≠0 → b≠0 → a*b≠0
當然,GPT-4也知道Lean,它可以提供一些有用的回答。
不過,因為自然數游戲中可用的工具集很有限,所以GPT-4對于這個游戲沒有直接的幫助,因為它提出的解決方案中涉及的方法,通常還沒有被納入游戲中。
不過,當他開始使用Lean的時候,GPT-4就變得非常有幫助了。
 圖片
圖片
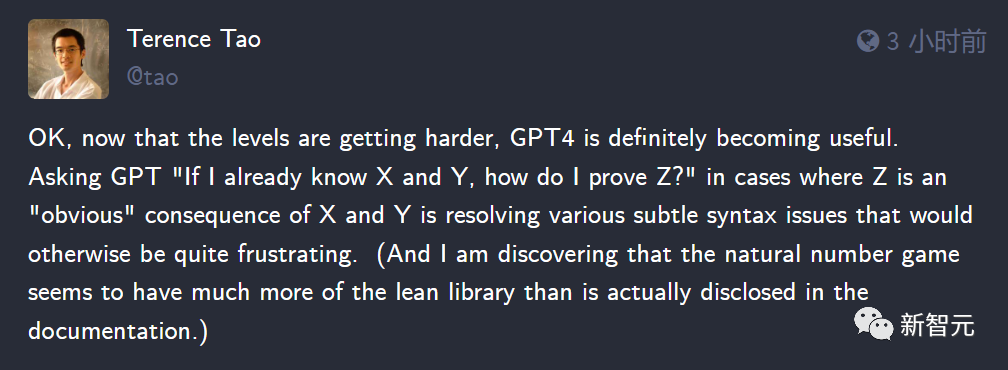
隨著關卡變得越來越難,GPT的作用開始逐漸顯現出來。
在Z顯而易見是X和Y的結果的情況下,如果向GPT提問——
如果我已經知道X和Y,該如何證明Z呢?
這個過程就解決了各種微妙的語法問題,否則這些問題會十分令人沮喪。
 圖片
圖片
而且,陶哲軒發現,自然數游戲中包含的Lean庫,似乎比文件中宣稱的要多得多。
GitHub Copilot,讓我不安
總之,AI工具輔助研究數學的奇跡,一次次讓陶哲軒稱贊不已,甚至發展到了讓他「不安」。
前不久陶哲軒發現,GitHub Copilot已經能夠預測到自己文章中數學論證的步驟了。
 圖片
圖片
在10月初,陶哲軒表示,Github Copilot的能力驚艷到他了。
而且他強調,并不是它的編碼能力,而是它編碼之外的補充其他內容的能力,經常能讓他喜出望外。
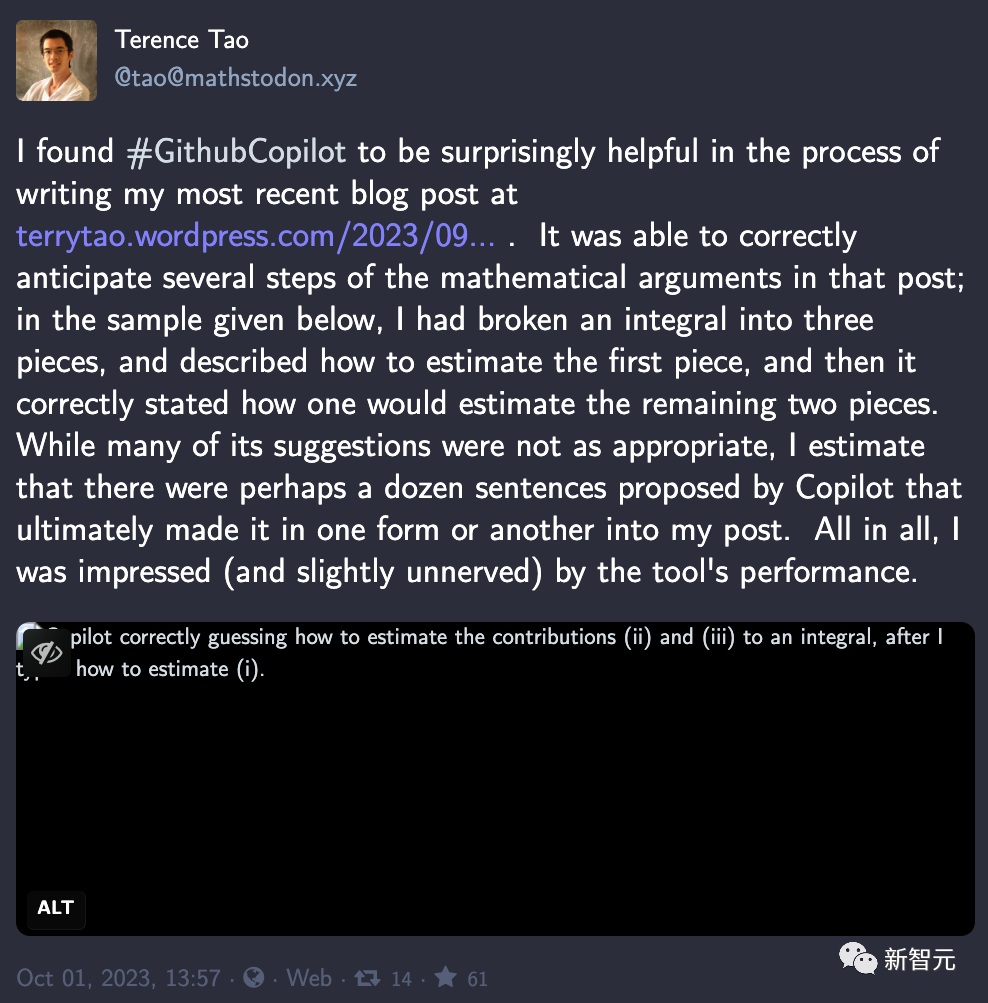
最近,他又稱贊到——
我發現Github Copilot在我最近撰寫博客文章的過程中出奇地有幫助。它能夠正確預測該帖子中數學論證的幾個步驟;在下面給出的示例中,我將積分分成三部分,并描述了如何估計第一部分,然后copilot正確地說明了如何估計其余兩部分。
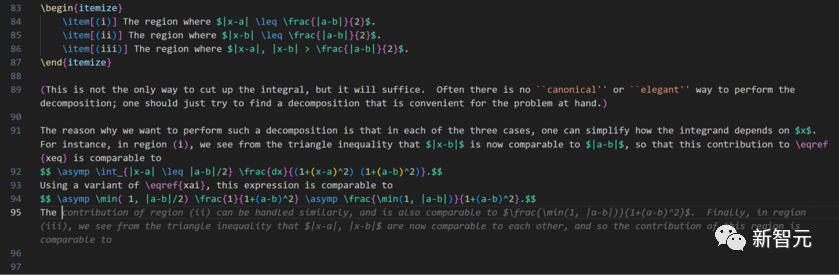 陶哲軒給出的例證
陶哲軒給出的例證
只要簡單說明一下如何對第一部分進行估計,剩下的工作GitHub Copilot就能完成了,這也太驚艷了!
對此,陶哲軒的評價是:「Copilot的性能給我留下了深刻的印象(并且讓我有點不安)」。
他補充說「雖然其中的許多建議并不那么合適,我估計Copilot可能建議了十幾句話,最終以某種形式出現在我的博客文章中。」
而他說的博客文章就是這篇關于「非負量的和或積分的上界」。
 圖片
圖片
博文地址:https://terrytao.wordpress.com/2023/09/30/bounding-sums-or-integrals-of-non-negative-quantities/
估計某個量的大小,是數分、概率論、組合學等領域中的常見問題,如估計函數、序列、結合等的和或積分。
因此陶哲軒這篇估計非負量的和或積分上界,探討的正是數學領域的重要問題。
 圖片
圖片
陶哲軒在博客中總結了3種估算大量非負量和以及積分的方法,如算術平均值-幾何平均值不等式、Holder不等式、Markov不等式等。
 圖片
圖片
其中的內容和代碼沒有關系,但是Github Copilot依然給出了讓陶哲軒都感到驚嘆的內容建議。
 圖片
圖片
能讓陶哲軒都感到有點不安的Github Copilot,源于Github和OpenAI的合作。
它主要功能是利用生成式AI的能力為程序提供編碼的建議,自動補充等編碼功能。而之所以它有如此強大的功能,和背后微軟,OpenAI的大量投入是分不開的。
最近外媒報道,微軟提供的Github Copilot每月10刀的訂閱服務,在算力成本上,每個用戶要讓微軟虧損20美元/月。
 圖片
圖片
文章地址:https://www.wsj.com/tech/ai/ais-costly-buildup-could-make-early-products-a-hard-sell-bdd29b9f?mod=followamazon
這些服務成本如此高昂的原因之一,是使用了最強大的AI模型,與普通的軟件或云服務相比,這些模型需要更多的電力,并對處理器的運行造成更大的壓力。
文章中甚至將現在的AI工具的能力和成本做了一個讓人繃不住的比喻:
「用AI去做文章總結就像開著蘭博基尼去送披薩一樣」。
足見現在科技巨頭們,為了讓用戶充分享受AI帶來的便利,真的是下了血本!
所以讓陶哲軒驚嘆的Github Copilot能在編碼之外還有如此強大的能力,也似乎不那么奇怪了。
AI如何輔助數學研究
顯然,現在所有人都已經意識到:AI具有巨大潛力,它可以通過指導猜想生成、協助形式化數學等方式為數學發展做出貢獻。
在9月26日舉行的一場關于使用AI輔助數學推理的網絡研討會上,眾數學大咖云集,一起討論了人工智能技術如何用于推進數學科學,跨學科合作如何開辟新的機會。
陶哲軒也參與了會議,并結合自己與AI合作的經歷談了自己的觀點。
 圖片
圖片
大會對于AI輔助數學研究,AI專家和數學家協作配合的新機會和新挑戰,都展開了充分地討論,可謂是干貨滿滿:
嘗試應用機器學習方法來輔助或完成形式數學論證,現在已經是人工智能應用的一個獨特領域
AI在輔助數學研究中的獨特之處在于,數學具有一種自我驗證的方法,可以用來檢查AI產生的結果,而其他AI任務通常需要人類參與來評估反饋的質量。
數學表達本身具有一種內在的準確性,因此機器學習在數學領域能夠在數據相對稀缺的情況下有效地推進工作,這使得AI在數學領域具備明顯的優勢。
在研討會上,多位數學領域專家進行了知識分享和交流。
 圖片
圖片
在使用機器學習協助數學發現方面,會議中數學家Heather提到了具體的幾個例子:
 圖片
圖片
(1) DeepMind和數學家合作,利用機器學習從大量數據中尋找模式,形成了關于模形的新猜想。
(2) Sutherland等數學家也使用機器學習在模形式的工作中找到了新公式。
(3) Adam Wagner使用機器學習來尋找圖論問題的反例。
(4) Javier Pena利用機器學習找到偏微分方程近似的數值解,以方便后續的嚴格數值方法的推進。
在使用AI輔助證明方面,會議提到形式化證明可以將一個大證明分解成小塊,不同人可以負責不同部分。
 圖片
圖片
這可能會開啟新的科研協作模式——計算機可以自動化證明中的某些步驟,已經有許多前沿的數學領域使用了這種模式。
這種形式化證明的過程有利于數學家以新方式與AI進行創造性的互動。
這也體現了AI協助數學發現和傳統數學研究的不同:既有大公司提供計算資源的大規模合作,也有小規模的個人之間的合作探索。
學界需要對這些不同的合作模式保持開放。
 圖片
圖片
會議中,還有多位學者討論了AI在數學翻譯中的應用
數學翻譯是指將一個數學問題從一個領域翻譯到另一個領域的等價表達,這是數學家解決問題的基本工具之一。
數學家以一個圖論問題為例。圖論問題可以翻譯成代數問題,兩者邏輯上是等價的,但表達上的術語和形式明顯不同。
AI轉換工具可以將一個看似毫無頭緒的問題,轉化成一個可以用已有技術來解決的問題。
還有學者進一步指出,證明思路到形式證明的轉換,以及形式證明到實際算法的轉換,也是一種翻譯過程。
鑒于AI在不同語言之間的翻譯上取得了巨大進展,未來可以研究如何應用機器學習來實現數學領域內的翻譯。
例如將不完整的證明草圖自動翻譯成可證明的形式表達。這是當前一個非常有前景的研究方向。
會議中多位數學家也強調了。由于數學翻譯能顯著拓展問題解決的視角,應用機器學習來實現數學翻譯將可能大大推進數學研究。
 圖片
圖片
AI專家和數學家進行跨界合作,需要面對的差異和挑戰
AI界和數學界,存在著諸多差異。
比如,機器學習研究者習慣處理大規模數據集,而數學家習慣于處理相對較少的數據。機器學習研究者注重在一類任務上的平均表現,而數學家則更關注單個案例的解釋。
另外,兩者的出版文化不同,機器學習界會公開發表絕大部分研究內容,數學界則不然。機器學習界普遍第一作者為主要貢獻者,數學界作者順序就比較隨機。
大規模合作項目的學術貢獻認定上,二者也存在差異。形式化研究使得每個參與者只負責一小塊,如何評價貢獻是一個新問題。
還有一個差異,是資源獲取方式。
機器學習需要大數據集和計算資源,數學家對這方面的需求就相對較少。如何使各界研究者公平獲取資源也會是一個問題。開源文化不同。機器學習界更看重開源共享,而數學界不一定。如何處理二者關系需要考量。
由于這是一個全新的交叉領域,雙方在一些根本理念和工作方式上存在差異,需要在合作中加以認識和調適,以實現更好的協同效果。
參考資料:
https://mathstodon.xyz/@tao/111206761117553482