清華校友用AI破解162個高數(shù)定理,智能體LeanAgent攻克困擾陶哲軒難題!
諾貝爾物理學獎和化學獎被AI「包圓」后,人們再次確信:基礎科學研究的范式,已經(jīng)被AI從根本上改變。
果然,就在剛剛,AI成功證明了162個以前未被證明的數(shù)學定理,再次印證了這一點。
 圖片
圖片
到目前為止,LLM仍然是靜態(tài)的,無法在線學習新知識,更別提證明高數(shù)定理了。
對此,來自加州理工、斯坦福和威大的研究人員提出了LeanAgent——一個終身學習,并能證明定理的AI智能體。
 圖片
圖片
論文地址:https://arxiv.org/abs/2410.06209
LeanAgent會根據(jù)數(shù)學難度優(yōu)化的學習軌跡課程,來提高學習策略。并且,它還有一個動態(tài)數(shù)據(jù)庫,有效管理不斷擴展的數(shù)學知識。
值得一提的是,整個學習過程中,它既能自我學習新知識,同時不會遺忘已具備的能力。
實驗結果發(fā)現(xiàn),LeanAgent從來自23個不同Lean代碼庫中,成功證明162個此前未被人類證明的數(shù)學定理。
相較于基于Lean數(shù)據(jù)微調大模型,LeanAgent性能直接飆升11倍。而且,綜合終身學習能力近94%。
其中,有許多是高等數(shù)學定理,比如具有挑戰(zhàn)性的抽象代數(shù)、代數(shù)拓撲。
它還展現(xiàn)出了從基本概念到高級主題清晰的學習過程。
同時,LeanAgent在穩(wěn)定性、反向遷移方面取得了卓越的成績,并且學習新任務還能提高以往任務的性能。
陶哲軒的證明,AI依然無解?
交互式定理證明器(ITPs),如Lean,已成為形式化和驗證數(shù)學證明的工具。
然而,使用ITPs構建形式化證明不僅復雜,且非常耗時。因為它需要極其詳細的證明步驟,并需要使用大量數(shù)學代碼庫。
諸如o1、Claude先進的大模型,在非形式化證明中,會產(chǎn)生幻覺。這愈加凸顯了,LLM在形式化數(shù)學證明中準確性、可靠性方面的重要性。
先前的一系列研究,探索了LLM也能夠生成完整的證明步驟。
比如,LeanDojo便是基于開源大模型構建的定理證明器。研究人員通過在特定數(shù)據(jù)集上,訓練微調大模型而來。
 圖片
圖片
項目地址:https://leandojo.org/
然而,形式化定理證明數(shù)據(jù)非常稀缺,進而阻礙了這一方法的泛化能力。
再比如,ReProver專門針對Lean定理證明代碼庫mathlib4微調的大模型。盡管這個數(shù)據(jù)庫包含了超10萬個形式化數(shù)學定理、定義,但它們分布僅覆蓋的是本科數(shù)學。
因此,ReProver在更具挑戰(zhàn)性問題——陶哲軒對多項式Freiman-Ruzsa(PFR)猜想的形式化,表現(xiàn)就會很差。
 圖片
圖片
https://terrytao.wordpress.com/2023/11/13/on-a-conjecture-of-marton/
并且,數(shù)學研究動態(tài)性,更是加劇了無法泛化的問題。
數(shù)學家們通常同時,或者交替在多個領域、項目中進行形式化。
比如,陶哲軒并行開啟多個項目,包括PFR猜想、實數(shù)對稱平均、經(jīng)典牛頓不等式、漸近分析的形式化。
Patrick Massot專注于形式化Scholze凝聚態(tài)數(shù)學,以及完美空間(Perfectoid Spaces)項目。
 圖片
圖片
這些例子突出了當前AI定理證明方法一個關鍵不足:
缺乏一個能夠隨時間在不同數(shù)學領域自適應、改進的AI系統(tǒng),特別是在Lean數(shù)據(jù)可用性有限的前提下。
與終身學習的相關性
至關重要的是,數(shù)學家們形式化過程與終身學習密切相關,即在不忘記的情況下學習多個任務。
然而,對于AI來說,一個重大挑戰(zhàn)便是「災難性遺忘」問題。
它們往往會學習新知識(新分布)后,直接丟失,甚至抹去了對舊知識(舊分布)的記憶。
而核心挑戰(zhàn)是,如何去平衡可塑性(學習和適應的能力)與穩(wěn)定性(保留現(xiàn)有知識的能力)。
當AI學習新任務時,可能會覆蓋了先前的學習信息。而若是為了增強穩(wěn)定,保留既有的知識,便會損害LLM獲取新技能的能力。
在數(shù)學形式化定理證明中,AI持續(xù)泛化能力的關鍵,便是在這兩者之間實現(xiàn)平衡。
LeanAgent:首個終身學習證明數(shù)學定理的AI智能體
基于以上難題,LeanDojo原班人馬團隊提出了LeanAgent,一個用于定理證明的全新終身學習框架。
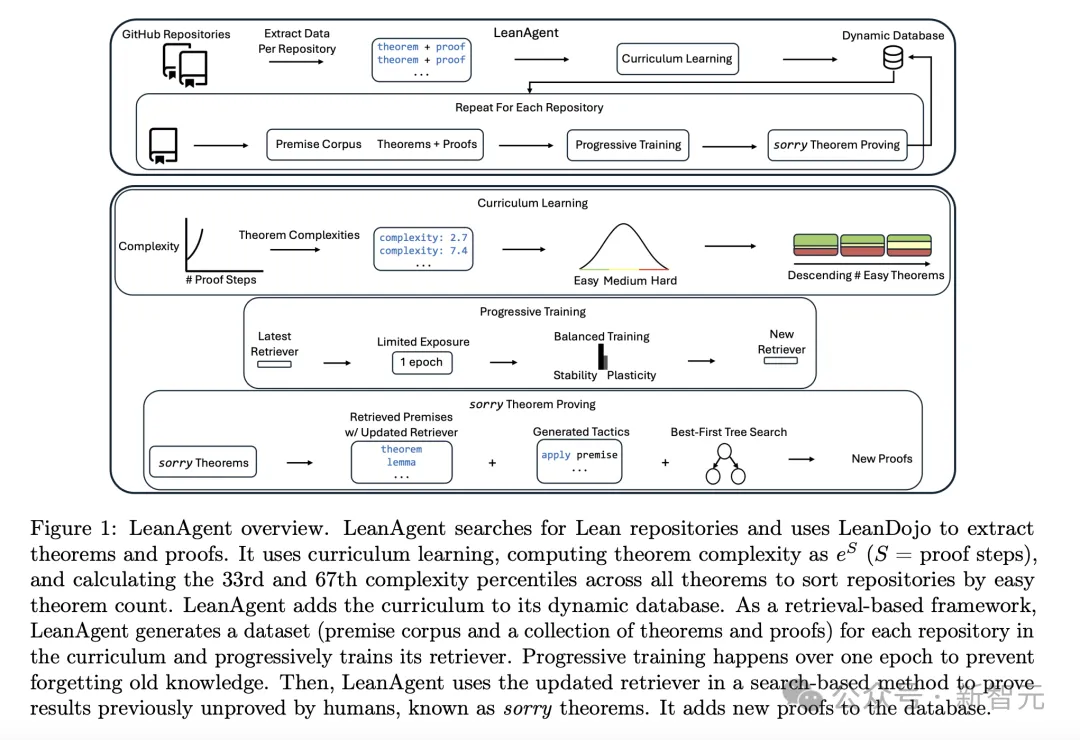
如下圖1所示,LeanAgent工作流包括了:
- 推導定理的復雜度,以計算學習課程
- 進行漸進訓練,在學習過程中平衡穩(wěn)定性和可塑性
- 利用最佳優(yōu)先樹搜索,來搜索sorry定理(人類尚未證明的定理)
當然,LeanAgent可與任何LLM結合使用,并且通過「檢索」來提高泛化能力。
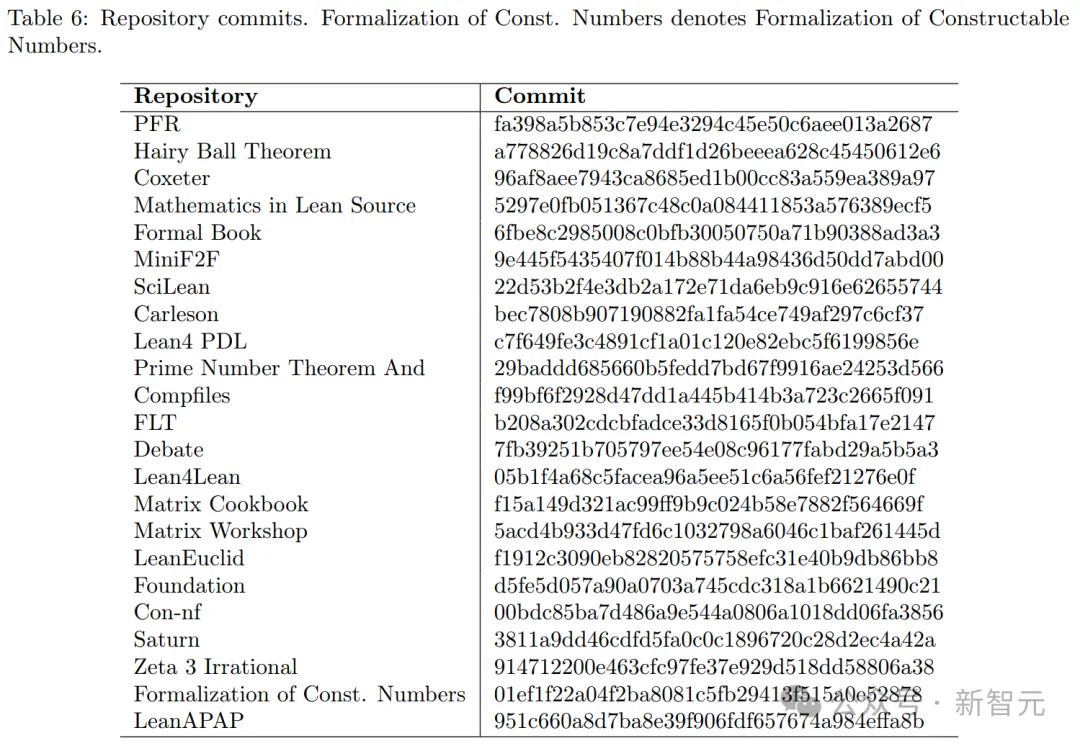
同時,LeanAgent包含了幾個關鍵的創(chuàng)新——
使用自定義動態(tài)數(shù)據(jù)庫,管理不斷擴展的數(shù)學知識;使用一種新穎課程學習(curriculum learning)策略,利用Lean證明結構,來學習更復雜的數(shù)學倉庫。
 圖片
圖片
對于AI災難性遺忘問題,研究人員采用了簡單的「漸進」訓練方法。
該方法讓LeanAgent能夠持續(xù)適應新的數(shù)學知識,同時還能保留先前的學習信息。
這一過程涉及了,在課程中每個倉庫生成的新數(shù)據(jù)集上,增量訓練檢索器。
從預訓練檢索器開始(比如基于ByT5 ReProver檢索器),LeanAgent在每個新數(shù)據(jù)集上,額外訓練一個epoch。
通過將漸進訓練限制在一個epoch,有助于平衡穩(wěn)定性和可塑性。
尤其是,漸進訓練對數(shù)據(jù)庫生成的每個數(shù)據(jù)集重復進行,逐步擴展LeanAgent知識庫。
它的優(yōu)勢是,增加了可能的證明狀態(tài)空間(其中狀態(tài)包括定理的假設和當前證明進展),同時向前提嵌入添加了新的前提。
不過,更復雜的終身學習方法,如彈性權重合并(EWC),使用Fisher信息矩陣來約束先前任務的重要權重,會導致過度可塑性。
這種不受控制的可塑性,是因為AI無法隨著定理復雜度的增加,而適應參數(shù)重要性。
它迫使AI在學習高級概念時,關鍵參數(shù)會發(fā)生快速變化。
因此,這些方法是無法適應數(shù)學定理不斷演變復雜性,也就無法適用在定理證明中的終身學習。
如前所述,在23個不同的Lean代碼庫中, LeanAgent在定理證明終身學習方面取得了優(yōu)越性。
它成功證明了162個sorry定理,其中許多來自高等數(shù)學。
比如,LeanAgent證明了來自PFR倉庫的困難sorry定理,并證明了抽象代數(shù)和代數(shù)拓撲中與Coxeter系統(tǒng)和毛球定理相關的挑戰(zhàn)性定理。
另外,研究人員還發(fā)現(xiàn),LeanAgent在定理證明中,展現(xiàn)出漸進學習的一面。
從最初證明基本的sorry定理,到后面證明了更復雜的定理。
而且,LeanAgent在只能證明新的sorry定理方面,比靜態(tài)ReProver基線高出多達11倍,同時保留了對已知定理證明的能力。
在定理證明中,作者還發(fā)現(xiàn)穩(wěn)定性(在不失去太多可塑性前提下),對于AI持續(xù)泛化到新倉庫至關重要。
反向遷移(BWT),即學習新任務改善先前學習任務的性能,也在定理證明中至關重要。
數(shù)學家需要一個既能持續(xù)泛化,又能持續(xù)改進的定理證明終身學習框架。
最后的消融實驗中,相較于7個終身學習框架,LeanAgent簡單的課程學習和漸進訓練組件,顯著提高了穩(wěn)定性和BWT得分。
最終,LeanAgent拿下了94%綜合終身學習的成績,幾乎接近完美。
這也揭示了,LeanAgent在持續(xù)泛化和改進的強大能力,以及卓越的sorry定理證明性能。
LeanAgent對數(shù)學知識的掌握
在終身學習過程中,LeanAgent展示了對基本代數(shù)結構和基本數(shù)學運算的深刻理解。
a)群和環(huán)論
LeanAgent證明了關于基本代數(shù)結構的定理。例如,MyGroup.mul_right_inv證明了將一個元素與其逆元素相乘等于單位元,而MyRing.add_right_cancel則展示了環(huán)加法的消去性質。
 圖片
圖片
b)初等數(shù)論
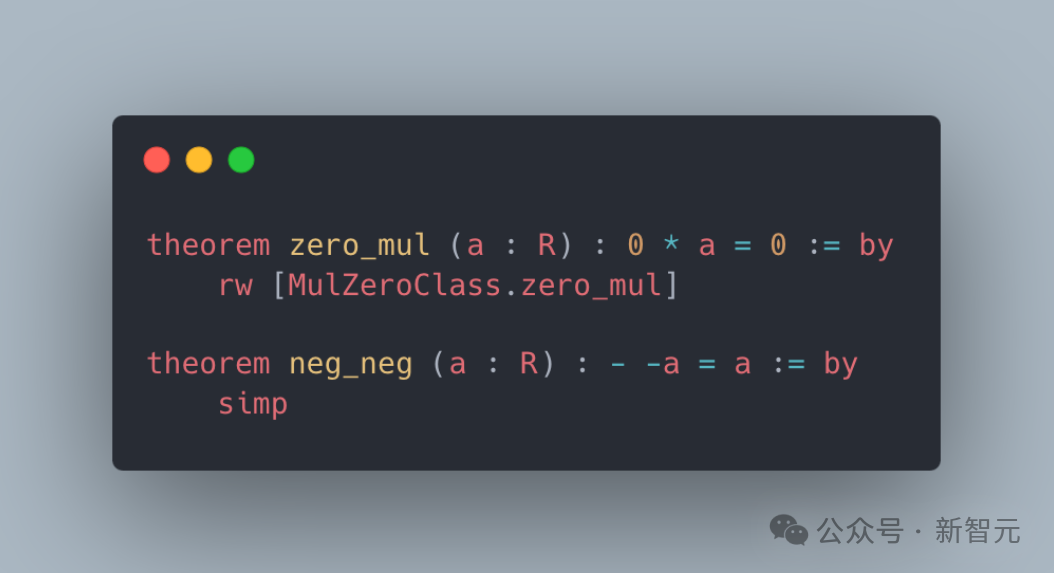
LeanAgent可以處理基本的算術屬性。例如,MyRing.zero_mul證明了零乘以任何數(shù)都是零,而MyRing.neg_neg則證明了負數(shù)的負數(shù)等于原數(shù)。
 圖片
圖片
c)序理論
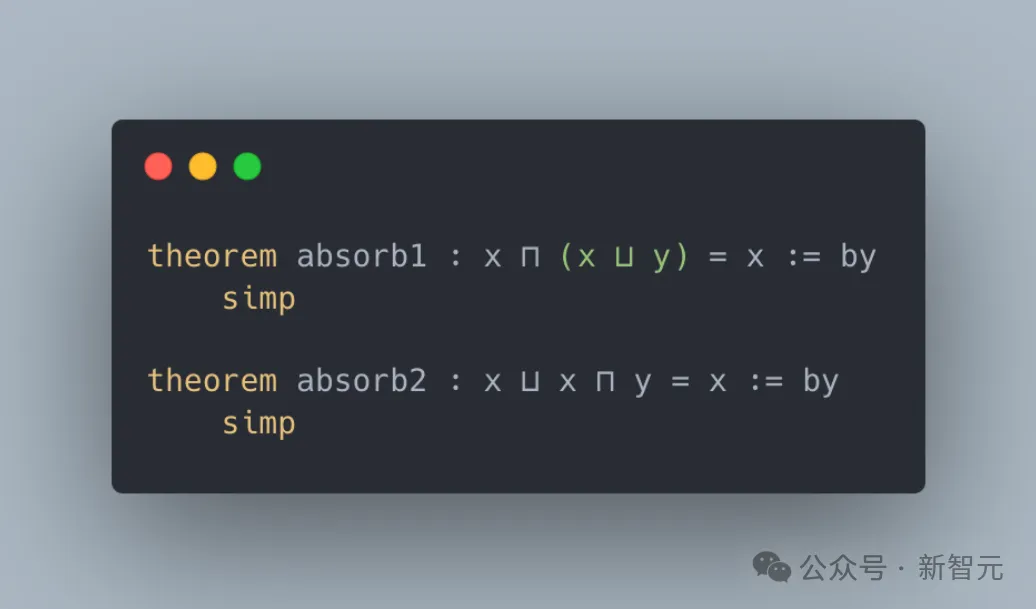
LeanAgent掌握了序理論的相關概念。例如,absorb 1證明了x與(x和y的上確界)的下確界總是等于x,而absorb2證明了x與(x和y的下確界)的上確界總是等于x。
 圖片
圖片
d)初等實分析
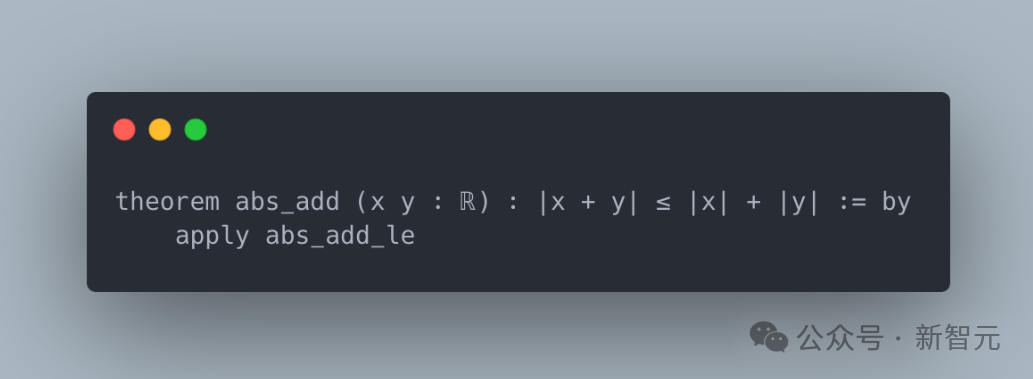
LeanAgent 展示了對實數(shù)及其絕對值性質的初步理解。例如,C03S05.MyAbs.abs_add證明了涉及實數(shù)的三角不等式。
 圖片
圖片
終身學習過程表明,LeanAgent已經(jīng)從基礎開始理解數(shù)學概念。而在這個過程結束后,它的數(shù)學推理能力有顯著提升。
比如證明了涉及多個量詞和條件的邊界和絕對值的復雜命題。
 圖片
圖片
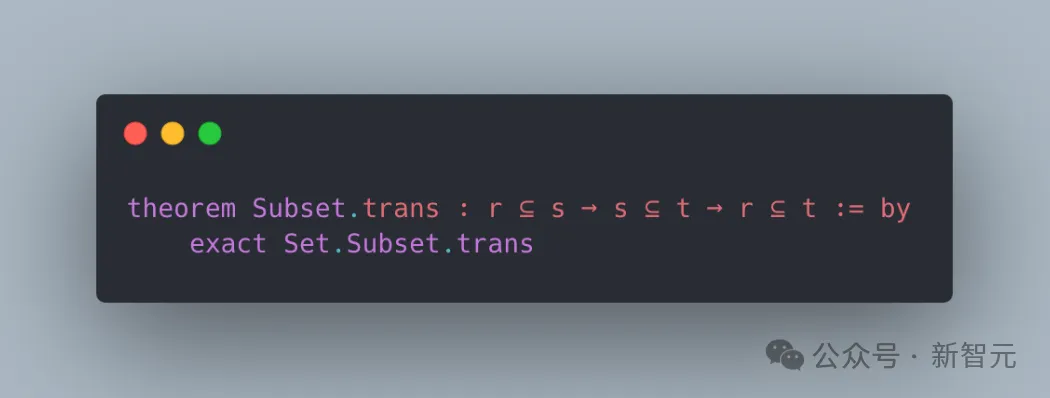
理解了抽象集合論的概念,證明了子集關系是傳遞的。
 圖片
圖片
方法
用于定理證明的有效終身學習策略,需要(a)最佳倉庫順序策略和(b)最佳學習策略。
通過課程學習,研究者解決了(a),以利用Lean證明的結構,并通過漸進式訓練來解決(b),以平衡穩(wěn)定性和可塑性。
LeanAgent由四個主要組件組成:課程學習、動態(tài)數(shù)據(jù)庫管理、檢索器的漸進式訓練和sorry定理證明。
課程學習
LeanAgent采用課程學習方法,學習逐漸增加復雜度的數(shù)學代碼庫。
這個過程優(yōu)化了LeanAgent的學習軌跡,讓它能夠在處理更高級的概念之前,先建立堅實的基礎知識。
具體步驟如下:
- 自動搜索并克隆GitHub上的Lean代碼庫。
- 使用LeanDojo提取每個代碼庫中定理、證明和依賴關系的細粒度信息。
- 使用公式eS計算每個定理的復雜度,其中S代表證明步驟的數(shù)量。對于沒有證明的sorry定理(即未完成證明的定理),賦予無限復雜度。
- 采用指數(shù)縮放,來解決隨著證明長度增加可能出現(xiàn)的證明路徑組合爆炸問題。
- 計算所有代碼庫中所有定理復雜度的第33百分位和第67百分位。
- 將非sorry定理分為三組:簡單(復雜度低于第33百分位)、中等(復雜度在第33百分位和第67百分位之間)和困難(復雜度高于第67百分位)。
- 按照代碼庫中包含的簡單定理數(shù)量對代碼庫進行排序,形成課程基礎。
LeanAgent從包含最多簡單定理的代碼庫開始學習。
動態(tài)數(shù)據(jù)庫管理
在建立課程后,研究者進行以下操作:
- 將排序后的代碼庫添加到LeanAgent的自定義動態(tài)數(shù)據(jù)庫中,使用LeanAgent提取的數(shù)據(jù)。
- 將每個定理的復雜度包含在動態(tài)數(shù)據(jù)庫中,以便未來課程中高效重用代碼庫。
- 對課程中的每個代碼庫,LeanAgent使用動態(tài)數(shù)據(jù)庫生成數(shù)據(jù)集,遵循與制作LeanDojo基準測試4相同的程序。
生成的數(shù)據(jù)集包括:
- 一系列定理及其證明
- 每個證明步驟的詳細注釋,說明該步驟如何改變證明的狀態(tài)
- 定理狀態(tài)信息,包括假設和證明進展
- 展示如何按順序使用特定的策略(函數(shù))和前提來證明定理
- 前提語料庫,作為事實和定義的參考庫
檢索模型的漸進式訓練
LeanAgent在新生成的數(shù)據(jù)集上,對其檢索模型進行漸進式訓練。
這種策略使LeanAgent能夠持續(xù)適應新數(shù)據(jù)集中前提的新數(shù)學知識,同時保留先前學習的信息,這對定理證明的終身學習至關重要。
漸進式訓練通過逐步整合每個代碼庫的新知識來實現(xiàn)這一目標。訓練過程如下:
- 起點選擇:雖然LeanAgent可以與任何LLM配合使用,但研究者選擇從ReProver的檢索模型開始。這是ByT5編碼器的微調版本,利用其從mathlib4獲得的一般預訓練知識。
- 新數(shù)據(jù)集訓練:在新數(shù)據(jù)集上額外訓練LeanAgent一個epoch(訓練周期)。這種有限的訓練有助于防止對新數(shù)據(jù)過擬合,同時允許LeanAgent學習重要的新信息。
- 嵌入預計算:在驗證之前,預先計算語料庫中所有前提的嵌入,以確保這些嵌入與LeanAgent的當前狀態(tài)一致。
- 模型評估:
- 計算可塑性:保存在前十個檢索到的前提(R@10)的驗證召回率最高的模型迭代。這是一個原始可塑性值,用于評估LeanAgent適應新數(shù)學類型的能力。
- 計算穩(wěn)定性:計算模型在所有先前漸進式訓練過的數(shù)據(jù)集上的平均測試R@10,作為原始穩(wěn)定性值。 - 重復過程:對從數(shù)據(jù)庫生成的每個數(shù)據(jù)集重復上述步驟,體現(xiàn)訓練的漸進性質。
漸進式訓練的效果:
- 將新的前提添加到前提嵌入中
- 增加可能的證明狀態(tài)空間
- 使LeanAgent能夠探索更多樣化的證明路徑
- 發(fā)現(xiàn)無法用原始知識庫產(chǎn)生的新證明
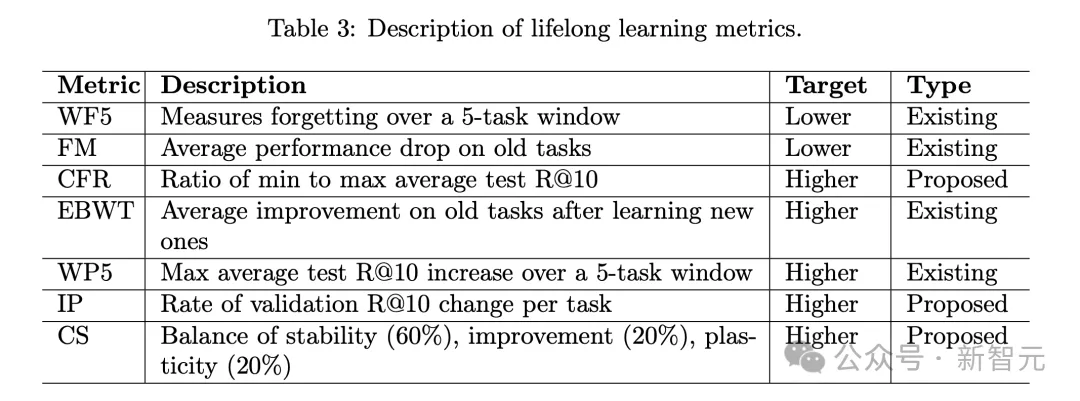
sorry定理的證明
對于每個sorry定理,LeanAgent AI智能體會通過最佳優(yōu)先樹搜索生成證明。具體步驟如下:
1. 前提檢索:
- 使用之前收集的整個前提語料庫的嵌入
- 基于當前證明狀態(tài)(表示為上下文嵌入)與前提的相似性,從前提語料庫中檢索相關前提
- 使用語料庫依賴圖進行過濾,確保只考慮當前文件可訪問的前提
2. 策略生成:
- 將檢索到的前提添加到當前狀態(tài)
- 使用束搜索生成策略候選
3. 狀態(tài)評估:
- 將每個策略候選通過Lean運行,獲得潛在的下一個狀態(tài)
- 每個成功的策略應用都會向證明搜索樹添加一條新邊
4. 策略選擇:
- 選擇具有最大累積對數(shù)概率的策略,即導致該狀態(tài)的策略序列的累積對數(shù)概率
5. 回溯處理:
- 如果搜索遇到無效路徑,進行回溯并探索替代路徑
6. 迭代過程:
- 重復上述步驟,直到滿足以下條件之一:a) 找到證明 b) 窮盡所有可能性 c) 達到10分鐘的時間限制
7. 結果處理:
- 如果LeanAgent找到證明,將其添加到動態(tài)數(shù)據(jù)庫中
- 新證明中添加的前提將包含在涉及當前代碼庫的未來前提語料庫中
- LeanAgent可以在未來的漸進式訓練中從新證明中學習,進一步改進其性能
如前所述,研究者對從數(shù)據(jù)庫生成的每個數(shù)據(jù)集重復這個過程,因此這種訓練具有漸進性質。
漸進式訓練將新的前提添加到前提嵌入中,并增加了可能的證明狀態(tài)空間。
這使LeanAgent能夠探索更多樣化的路徑來證明定理,發(fā)現(xiàn)它無法用原始知識庫產(chǎn)生的新證明。
實驗
 圖片
圖片
sorry定理的證明
研究者比較LeanAgent AI智能體在持續(xù)學習過程中和之后能夠證明的sorry定理,并與ReProver基準進行對比。
選擇ReProver作為基準,是因為在實驗中使用了它的檢索器作為LeanAgent的初始檢索器。
然而,由于定理證明難度的非線性特性,研究者避免在LeanAgent和ReProver之間進行簡單的百分比比較。
值得注意的是,LeanAgent在多個代碼庫中顯著優(yōu)于基準的性能,讓它能夠證明越來越難的定理。
此外,sorry定理缺乏已知的證明,因此證明一個sorry定理,對數(shù)學研究具有重要價值。
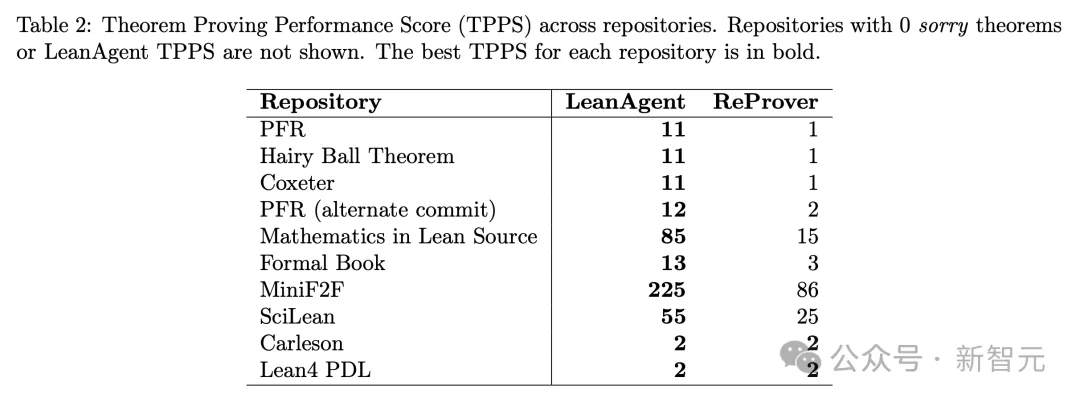
基于以上考慮,研究者提出了一個定理證明性能得分(Theorem Proving Performance Score,TPPS),特別強調新證明的sorry定理。
TPPS的計算方法如下:
- LeanAgent TPPS = (# ReProver Theorems Proved) + (# New Theorems Proved * X) + 1
- ReProver TPPS = (# ReProver Theorems Proved) + 1
- improvement Factor = (LeanAgent TPPS) / (ReProver TPPS)
其中,X代表證明新定理的重要性權重。考慮到基礎算術和抽象代數(shù)之間的巨大難度差距,研究者選擇了X = 10。
此外,LeanAgent AI智能體的一個使用場景,是在學習完一個課程后在新的代碼庫中進行形式化(即將數(shù)學概念和證明轉化為計算機可驗證的形式)。
研究者通過在MiniF2F上逐步訓練來展示這一點。需要注意的是,我們選擇了MiniF2F代碼庫的Lean4版本,并忽略了其驗證集和測試集的劃分(原因詳見附錄A.5)。
數(shù)學家可以使用LeanAgent進行以下兩步操作:
1. 學習初始課程A
2. 學習子課程B
然后,LeanAgent可以幫助數(shù)學家并行地形式化課程A+B中的代碼庫。
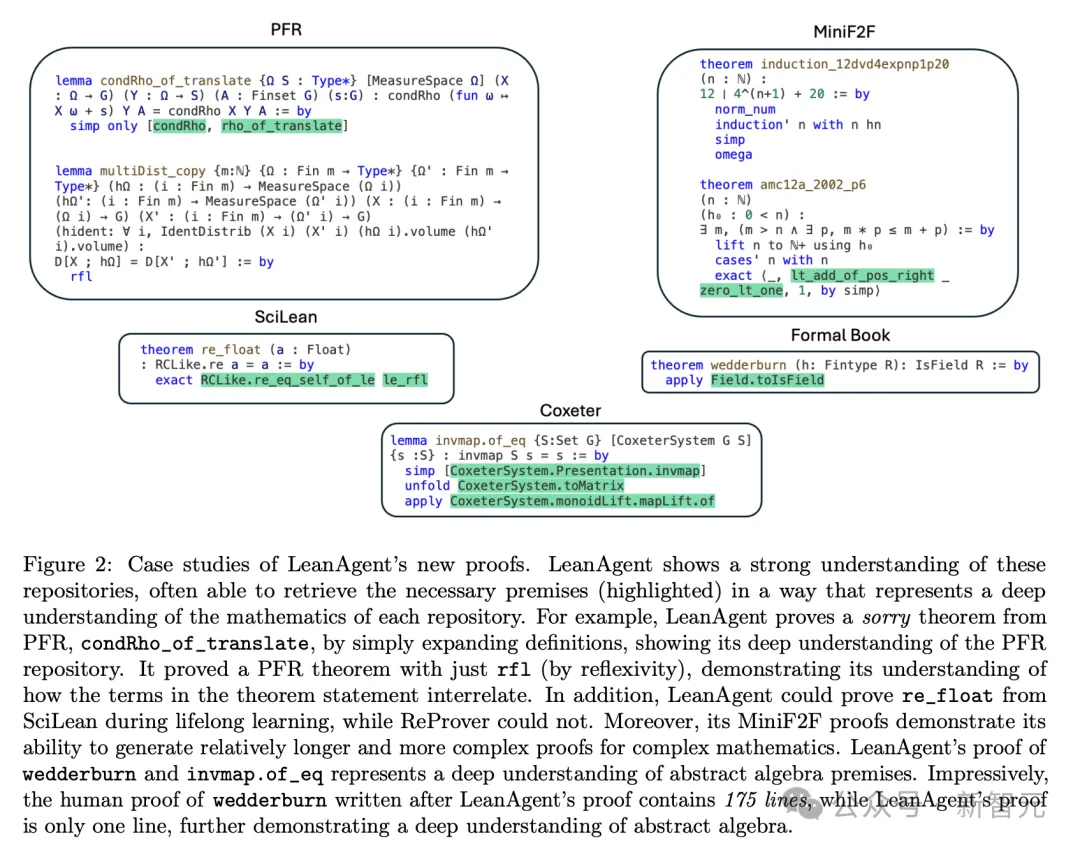
為了演示這種情況,研究者在8個代碼庫組成的子課程B上繼續(xù)訓練LeanAgent。結果見表2,案例研究見圖2。
 圖片
圖片
 圖片
圖片
LeanAgent在多個代碼庫中,展示了持續(xù)的泛化能力和定理證明能力的提升。
在終身學習結束時,LeanAgent相比ReProver的改進因子如下:
- PFR:11倍
- Mathematics in Lean Source:5.67倍
- MiniF2F:2.63倍
- SciLean:2.2倍
- Hairy Ball定理:11倍
- Coxeter:11倍
- Formal Book:4.33倍
在大多數(shù)情況下,LeanAgent的證明是ReProver所證明的sorry定理的超集。LeanAgent的學習進展從基本概念(如算術、簡單代數(shù))逐步深入到高級主題(如抽象代數(shù)、拓撲學)。
1. PFR:
LeanAgent AI智能體能夠證明這個前沿代碼庫中的一個sorry定理,而ReProver做不到。它還能泛化到不同的代碼提交,僅使用rfl策略就能證明ReProver無法證明的定理。有趣的是,LeanAgent對PFR代碼庫中的邏輯操作理解得足夠深入,能夠用「0 = 1」這樣的占位符定理語句,證明5個sorry定理。
2. SciLean:
在終身學習過程中,LeanAgent證明了與基本代數(shù)結構、線性和仿射映射以及測度論基礎相關的定理。到終身學習結束時,它掌握了高級函數(shù)空間、復雜雙射和抽象代數(shù)結構的概念。
3. Mathematics in Lean Source:
在終身學習過程中,LeanAgent證明了關于基本代數(shù)結構和基本算術性質的定理。到終身學習結束時,它能夠證明涉及量詞操作、集合論和關系的復雜定理。
4. MiniF2F:
ReProver展示了在基礎算術、初等代數(shù)和簡單微積分方面的熟練程度。然而,到終身學習結束時,LeanAgent掌握了高級數(shù)論、復雜代數(shù)、復雜微積分和分析、抽象代數(shù)以及復雜歸納法。
5. 子課程:
- Formal Book代碼庫:LeanAgent從證明基本實分析和數(shù)論定理進步到掌握高級抽象代數(shù),其證明Wedderburn小定理就是一個例證。
- Coxeter代碼庫:LeanAgent證明了一個關于Coxeter系統(tǒng)的復雜引理,展示了它在群論方面的熟練程度。
- Hairy Ball定理代碼庫:LeanAgent證明了該定理的一個關鍵步驟,展示了對代數(shù)拓撲的理解。
LeanAgent能夠證明這些令人印象深刻的定理,表明它比ReProver具有更高級的定理證明能力。
終身學習分析
因為文獻中不存在其他用于定理證明的終身學習框架,因此研究者進行了一項消融研究,使用七個終身學習指標,來展示LeanAgent AI智能體在處理穩(wěn)定性-可塑性權衡方面的優(yōu)越性。
這些結果有助于解釋LeanAgent AI智能體在sorry定理證明性能方面的優(yōu)勢。
研究者為原始的14個代碼庫課程計算了這些指標。
具體來說,消融研究包括七個額外的設置,這些設置由學習和數(shù)據(jù)集選項組合而成。學習設置的選項是有或沒有EWC的漸進式訓練。
數(shù)據(jù)集設置涉及數(shù)據(jù)集順序和構建。數(shù)據(jù)集順序的選項包括單一代碼庫或合并所有,其中每個數(shù)據(jù)集由所有先前的代碼庫和新的代碼庫組成。
考慮到GitHub上按星級計數(shù)最受歡迎的代碼庫,數(shù)據(jù)集構建的選項包括受歡迎度順序或課程順序。
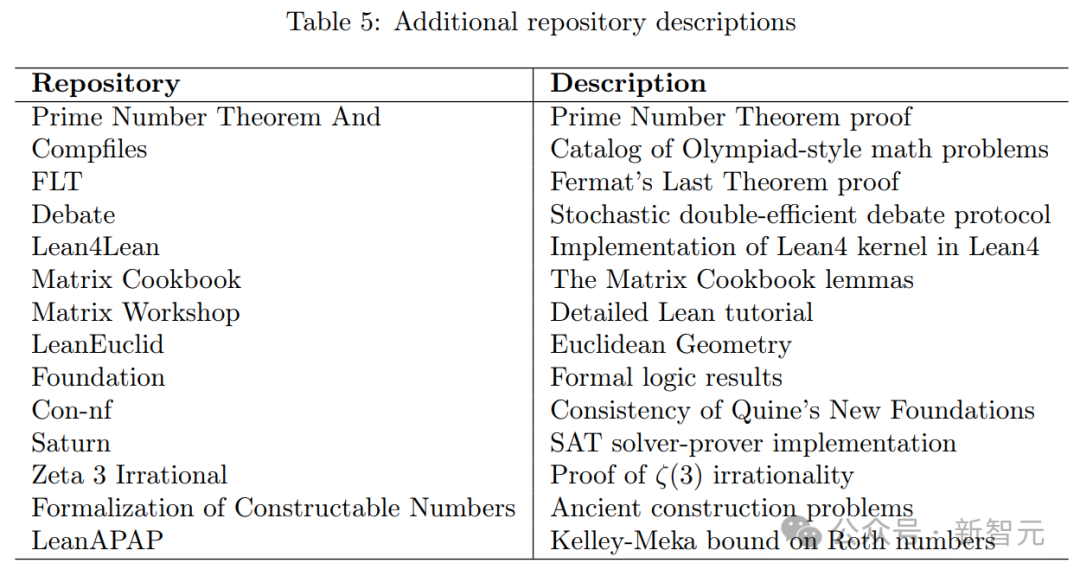 圖片
圖片
 圖片
圖片
研究者使用了以下七個終身學習指標:
1. 窗口遺忘5(WF5)
2. 遺忘度量(FM)
3. 災難性遺忘恢復力(CFR)
4. 擴展反向遷移(EBWT)
5. 窗口可塑性5(WP5)
6. 增量可塑性(IP)
7. 綜合得分(CS)
他們引入了三個新指標,來解決定理證明中終身學習的特定方面:
- 災難性遺忘恢復力(CFR):這個指標捕捉了LeanAgent AI智能體在其最弱任務上,相對于其最佳表現(xiàn)保持性能的能力,這在存在多樣化數(shù)學領域的情況下至關重要。
- 增量可塑性(IP):IP提供了比總體措施更細粒度的可塑性視圖,并對任務順序敏感,這在定理證明的終身學習中特別相關。
- 綜合得分:目前應該還沒有廣泛建立的綜合指標能夠提供一個單一的穩(wěn)定性-可塑性權衡得分,包含表3中的前六個指標。
因此,研究者提出了一個綜合得分:Composite Score = 0.2 · (1 ? WF5_norm) + 0.2 · (1 ? FM_norm) + 0.1 · WP5_norm + 0.1 · IP_norm + 0.2 · EBWT_norm + 0.2 · CFR_ norm
 圖片
圖片
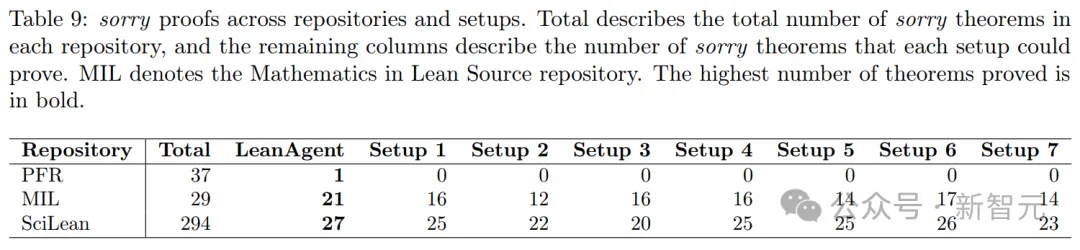
此外,這些指標在合并所有策略中衡量的是累積知識改進而不是孤立的任務表現(xiàn)。
 圖片
圖片
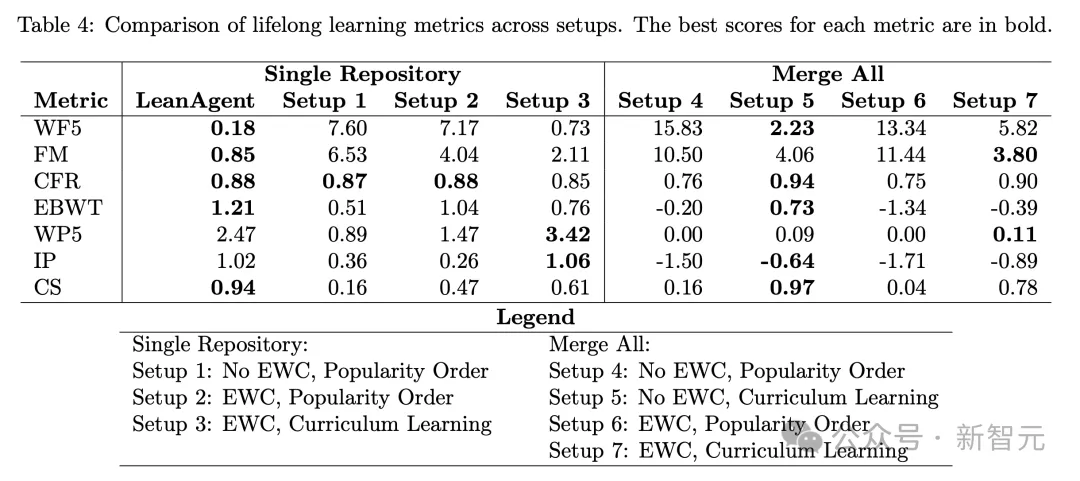
1. 單一代碼庫分析
表4呈現(xiàn)了,單一代碼庫的結果。
LeanAgent智能體在多項指標上,展現(xiàn)出卓越的穩(wěn)定性。其WF5指標比下一個最佳設置低75.34%,表明它能更有效地在一個時間窗口內保持性能。
LeanAgent FM得分比設置3還要低59.97%,展示了其對災難性遺忘的強大抵抗力。
此外,LeanAgent智能體、設置1和設置2中,都表現(xiàn)出高度一致的不會出現(xiàn)災難性遺忘,CFR值均超過0.87,差異極小(僅±0.01)。
這恰恰凸顯了,LeanAgent智能體隨時間持續(xù)泛化的能力。
另外,它EBWT高出16.25%,進而表明其具備了隨時間持續(xù)改進的能力。
 圖片
圖片
相比之下,設置3表現(xiàn)出更高可塑性。
它的WP5比LeanAgent AI 智能體高出38.26%,表明其在一個時間窗口內,快速適應新任務的能力更強。
設置3 IP 比LeanAgent智能體高出3.98%相輔相成,暗示了隨著時間推移,其在新任務上改進更為顯著。
然而,這些可塑性的提升是以極大代價換來的:設置3產(chǎn)生了更嚴重的災難性遺忘,可從其與LeanAgent智能體相比明顯較差的穩(wěn)定性指標可以看出。
設置3中過度的可塑性,源于EWC無法隨定理復雜性增加而調整參數(shù)重要性。
EWC保留了對簡單定理重要的參數(shù),但這些參數(shù)可能對更復雜的定理,并不關鍵。
因此,這些保留的參數(shù)抗拒變化,而其他參數(shù)為復雜定理快速變化。這迫使模型整體變得更具可塑性,在處理新的復雜定理時嚴重依賴非保留參數(shù)。
LeanAgent AI 智能體在綜合得分上表現(xiàn)出卓越性能,能夠在適應新任務的同時,保持已有知識,使其成為單一代碼庫設置中最適合終身學習智能體。
2. 合并所有分析
接下來,研究人員分析了表4中的合并所有設置。
設置5的WF5指標比下一個最佳設置(設置7)低61.68%,表明設置5在不斷擴大的數(shù)據(jù)集中最有效地實現(xiàn)可塑性和穩(wěn)定性平衡。
此外,設置5的CFR得分比設置7高3.77%,再次展示了面對不斷擴大、可能更復雜的數(shù)據(jù)集時的高度且一致的抵抗力。
然而,設置7的FM得分比設置5低6.44%,展示了其在早期數(shù)據(jù)點上能夠保持已有知識的能力。
此外,設置5是唯一一個EBWT為正的設置,表明學習新任務可以提高整個歷史數(shù)據(jù)集的性能。其他設置的EBWT為負,表明在學習新任務后,早期任務的性能有所下降。
只有設置5和7的WP5不為0,表明它們有能力適應合并數(shù)據(jù)集不斷增加的復雜性。
設置4和6為0數(shù)值表明,在處理合并數(shù)據(jù)時,按受歡迎程度排序難以顯示改進。然而,盡管設置5的IP得分最高,比設置7高27.75%,但所有4個設置的IP值都為負。
這表明驗證R@10隨時間推移而下降,說明合并所有策略難以保持性能。
設置5的高綜合得分表明,它在平衡保留早期知識與適應合并數(shù)據(jù)集中的新數(shù)據(jù)方面表現(xiàn)最佳。然而,其負IP值表明其方法存在根本性問題。
3. 比較分析和洞見
盡管這些指標在單一代碼庫和合并所有設置中有不同的解釋,但研究者表示,仍然可以通過關注整體趨勢和相對表現(xiàn),來進行一些有意義的比較。
研究者注意到,合并所有設置中的負IP值表明存在重大問題。
這個缺點超過了其他指標所顯示的潛在優(yōu)勢,因為它揭示了在持續(xù)增長的數(shù)據(jù)集中無法保持和改善性能的根本問題。
相比之下,LeanAgent展示了正IP值,表明其能夠有效吸收新知識。
這一特點,再加上其相對于其他單一代碼庫方法更優(yōu)越的穩(wěn)定性和EBWT指標,表明LeanAgent比設置5更適合實現(xiàn)持續(xù)的泛化能力和性能改進。
4. 與sorry定理證明性能的一致性
這種終身學習分析與LeanAgent在sorry定理證明方面的性能表現(xiàn)是一致的。
LeanAgent優(yōu)越的穩(wěn)定性指標(WF5、FM和CFR),解釋了它在不同數(shù)學領域保持性能的能力,這一點從它成功證明來自SciLean、Mathematics in Lean Source和PFR等不同代碼庫的定理中就可以被證實。
其高EBWT分數(shù)與它在定理證明中從基本概念到高級主題的進展相一致。
雖然LeanAgent相比某些設置顯示出略低的可塑性(WP5和IP),但這種權衡實際上導致了更好的整體性能。這一點體現(xiàn)在它能夠證明比其他方法更廣泛的sorry定理集合。
由持續(xù)泛化能力、持續(xù)改進和可塑性組成的綜合得分,進一步證實了LeanAgent在定理證明的終身學習方面具有全面的優(yōu)勢。
作者介紹
Peiyang Song
 圖片
圖片
Peiyang Song是加州理工學院(Caltech)計算機科學的本科生,由Steven Low教授的指導。同時也是斯坦福人工智能實驗室(SAIL)的研究員,在計算與認知實驗室(CoCoLab)由Noah Goodman教授指導。
他的研究方向是機器推理,特別是用于數(shù)學和代碼生成的AI。此前,從事過高能效機器學習系統(tǒng)和機器翻譯的研究。
Chaowei Xiao

Chaowei Xiao是威斯康星大學麥迪遜分校的助理教授,同時也是英偉達的研究員。
他的研究方向是探索LLM系統(tǒng)的安全性和安全保障,以及LLM在不同應用領域中的作用。
此前,他在密歇根大學安娜堡分校獲得博士學位,并在清華大學獲得學士學位。












































