近日，一篇名為《GFlowNet Foundations》的論文引發了人們的關注，這是一篇圖靈獎得主 Yoshua Bengio 一作的新研究，論文長達 70 頁。

在 Geoffrey Hinton 的「膠囊網絡」之后，深度學習的另一個巨頭 Bengio 也對 AI 領域未來的方向提出了自己的想法。在該研究中，作者提出了名為「生成流網絡」（Generative Flow Networks，GFlowNets）的重要概念。

[[436303]]

GFlowNets 靈感來源于信息在時序差分 RL 方法中的傳播方式（Sutton 和 Barto，2018 年）。兩者都依賴于 credit assignment 一致性原則，它們只有在訓練收斂時才能實現漸近。由于狀態空間中的路徑數量呈指數級增長，因此實現梯度的精確計算比較困難，因此，這兩種方法都依賴于不同組件之間的局部一致性和一個訓練目標，即如果所有學習的組件相互之間都是局部一致性的，那么我們就得到了一個系統，該系統可以進行全局估計。

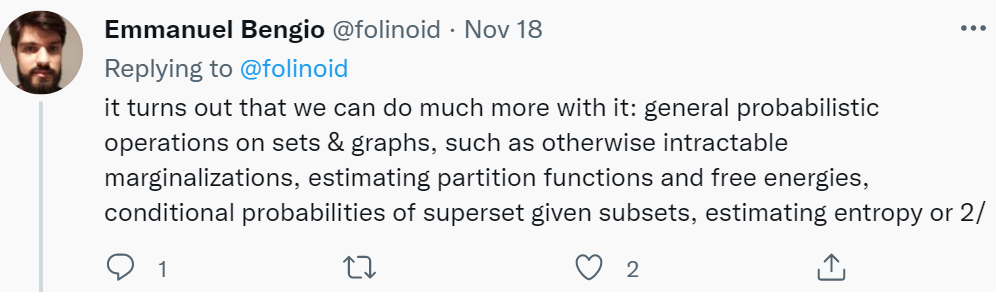
至于 GFlowNets 作用，論文作者之一 Emmanuel Bengio 也給出了一些回答：「我們可以用 GFlowNets 做很多事情：對集合和圖進行一般概率運算，例如可以處理較難的邊緣化問題，估計配分函數和自由能，計算給定子集的超集條件概率，估計熵、互信息等。」

本文為主動學習場景提供了形式化理論基礎和理論結果集的擴展，同時也為主動學習場景提供了更廣泛的方式。GFlowNets 的特性使其非常適合從集合和圖的分布中建模和采樣，估計自由能和邊緣分布，并用于從數據中學習能量函數作為馬爾可夫鏈蒙特卡洛（Monte-Carlo Markov chains，MCMC）一個可學習的、可分攤（amortized）的替代方案。

GFlowNets 的關鍵特性是其學習了一個策略，該策略通過幾個步驟對復合對象 s 進行采樣，這樣使得對對象 s 進行采樣的概率 P_T (s) 與應用于該對象的給定獎勵函數的值 R(s) 近似成正比。一個典型的例子是從正例數據集訓練一個生成模型，GFlowNets 通過訓練來匹配給定的能量函數，并將其轉換為一個采樣器，我們將其視為生成策略，因為復合對象 s 是通過一系列步驟構造的。這類似于 MCMC 方法的實現，不同的是，GFlowNets 不需要在此類對象空間中進行冗長的隨機搜索，從而避免了 MCMC 方法難以處理模式混合的難題。GFlowNets 將這一難題轉化為生成策略的分攤訓練（amortized training）來處理。

本文的一個重要貢獻是條件 GFlowNet 的概念，可用于計算不同類型（例如集合和圖）聯合分布上的自由能。這種邊緣化還可以估計熵、條件熵和互信息。GFlowNets 還可以泛化，用來估計與豐富結果 (而不是一個純量獎勵函數) 相對應的多個流，這類似于分布式強化學習。

本文對原始 GFlowNet （Bengio 等人，2021 年）的理論進行了擴展，包括計算變量子集邊緣概率的公式（或自由能公式），該公式現在可以用于更大集合的子集或子圖 ；GFlowNet 在估計熵和互信息方面的應用；以及引入無監督形式的 GFlowNet（訓練時不需要獎勵函數，只需要觀察結果）可以從帕累托邊界進行采樣。

盡管基本的 GFlowNets 更類似于 bandits 算法（因為獎勵僅在一系列動作的末尾提供），但 GFlowNets 可以通過擴展來考慮中間獎勵，并根據回報進行采樣。GFlowNet 的原始公式也僅限于離散和確定性環境，而本文建議如何解除這兩種限制。最后，雖然 GFlowNets 的基本公式假設了給定的獎勵或能量函數，但本文考慮了 GFlowNet 如何與能量函數進行聯合學習，為新穎的基于能量的建模方法、能量函數和 GFlowNet 的模塊化結構打開了大門。

論文地址：https://arxiv.org/pdf/2111.09266.pdf

機器之心對這篇論文的主要章節做了簡單介紹，更多細節內容請參考原論文。

GFlowNets：學習流（flow）

研究者充分考慮了 Bengio et al. (2021)中引入的一般性問題，在這些問題中給出了一些關于流的約束或偏好。研究者的目標是使用估計量 Fˆ(s)和 Pˆ(s→s'|s)找到最能匹配需求的函數，如狀態流函數 F(s)或轉移概率函數 P(s→s' |s)，這些可能不符合 proper flow。因此，他們將這類學習機器稱為 Generative Flow Networks（簡稱為 GFlowNets）。

GFlowNets 的定義如下：

需要注意的是，GFlowNet 的狀態空間（state-space）可以輕松修改以適應底層狀態空間，其中轉換（transition）不會形成有向無環圖（directed acyclic graph, DAG）。

對于從終端流（Terminal Flow）估計轉換概率，在 Bengio et al. (2021)的設置中， 研究者得到了與「作為狀態確定性函數的終端獎勵函數 R 」相對應的終端流：

這樣一來就可以擴展框架并以各種方式處理隨機獎勵。

GFlowNets 可以作為 MCMC Sampling 的替代方案。GFlowNet 方法分攤前期計算以訓練生成器，為每個新樣本產生非常有效的計算（構建單個配置，不需要鏈）。

流匹配和詳細的平衡損失。為了訓練 GFlowNet，研究者需要構建一個訓練流程，該流程可以隱式地強制執行約束和偏好。他們將流匹配（flow-matching）或細致平衡條件（detailed balance condition）轉換為可用的損失函數。

對于獎勵函數，研究者考慮了「獎勵是隨機而不是狀態確定性函數」的設置。如果有一個像公式 44 中的獎勵匹配損失，則終端流 F(s→s_f)的有效目標是預期獎勵 E_R[R(s)，因為這是給定 s 時最小化 R(s)上預期損失的值。

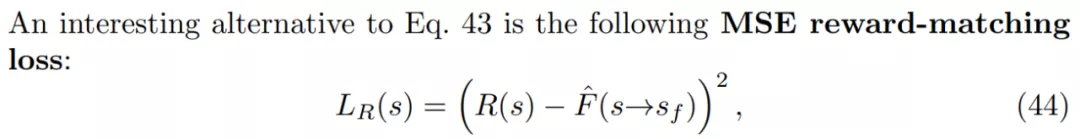
如果有一個像公式 43 中的獎勵匹配損失，終端流 log F(s→s_f)的 log 有效目標是 log-reward E_R[log R(s)]的預期值。這表明了使用獎勵匹配損失時，GFlowNets 可以泛化至匹配隨機獎勵。

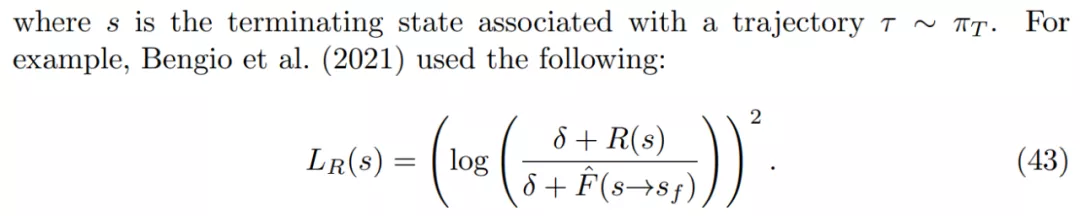
此外，GFlowNets 可以像離線強化學習一樣離線訓練。對于 GFlowNets 中的直接信用分配（Direct Credit Assignment），研究者認為可以將使用 GFlowNet 采樣軌跡的過程等同于在隨機循環神經網絡中采樣狀態序列。讓事情變得更復雜的原因有兩個，其一這類神經網絡不直接輸出與某個目標匹配的預測，其二狀態可能是離散（或者離散和連續共存）的。

條件流和自由能

本章主要介紹了條件流（Conditional flows）和自由能（Free energies）。

流的一個顯著特性是：如果滿足細致平衡或流匹配條件，則可以從初始狀態流 F(s_0) 恢復歸一化常數 Z（推論 3）。Z 還提供了與指定了終端轉換流的給定終端獎勵函數 R 相關聯的配分函數（partition function）。下圖展示了如何條件化 GFlowNet，給定狀態 s，考慮通過原始流（左）和轉移流來創建一組新的流（右）。

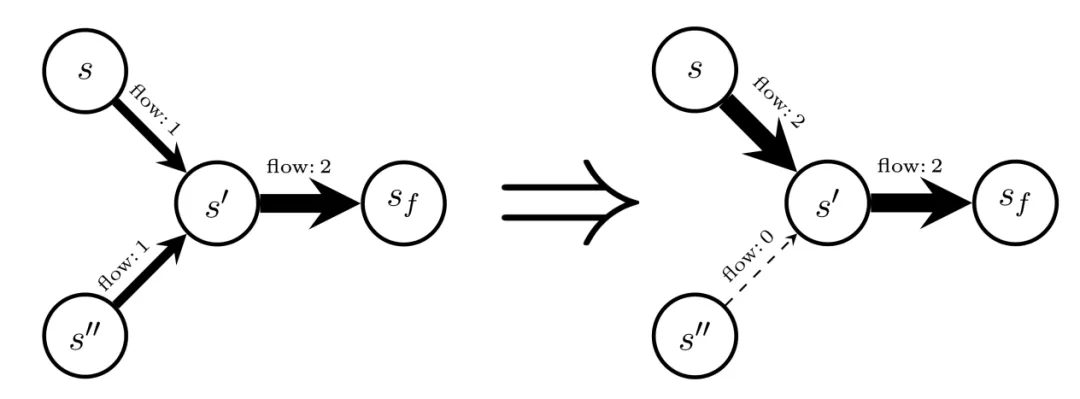
自由能是與能量函數相關的邊緣化操作（即對大量項求和）的通用公式。研究者發現對自由能的估計為有趣的應用打開了大門，以往成本高昂的馬爾可夫鏈蒙特卡洛（Markov chain Monte Carlo, MCMC）通常是主要方法。

自由能 F(s)的狀態定義如下：

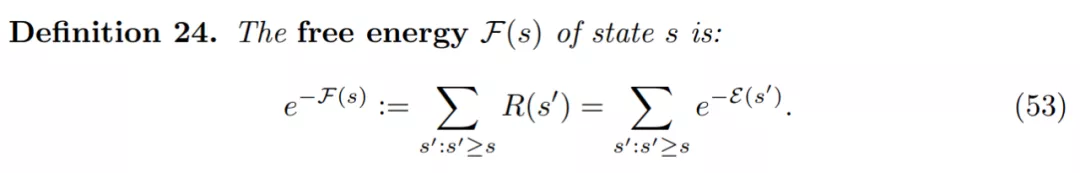
如何估計自由能呢？讓我們考慮條件式 GFlowNet 的一種特殊情況，它允許網絡估計自由能 F(s)。為此，研究者提議訓練一個條件式 GFlowNet，其中條件輸入 x 是軌跡中較早的狀態 s。

狀態條件式 GFlowNet 的定義如下，并且將 F(s|s)定義為 conditional state self-flow。

研究者表示，使用 GFlowNet 可以訓練基于能量的模型。具體地，GFlowNet 被訓練用于將能量函數轉換為逼近對應的采樣器。因此，GFlowNet 可以用作 MCMC 采樣的替代方法。

此外，GFlowNet 還可用于主動學習。Bengio et al. (2021)使用的主動學習方案中，GFlowNet 被用于對候選 x 進行采樣，其中研究者預計獎勵 R(x)通常很大，這是因為 GFlowNet 與 R(x)成比例地采樣。

多流、分布式 GFlowNets、無監督 GFlowNets 和帕累托 GFlowNets

與分布式強化學習類似，非常有趣的一點是，泛化 GFlowNets 不僅可以捕獲可實現的最終獎勵的預期值，還能得到其他分布式統計數據。更一般地講，GFlowNets 可以被想象成一個族（family），其中每一個都可以在自身流中對感興趣的特定的未來環境結果進行建模。

下圖為以結果為條件的（outcome-conditioned）GFlowNet 的定義：

在實踐中，GFlowNet 永遠無法完美地訓練完成，因此應當將這種以結果為條件的 GFlowNet 與強化學習中以目標為條件的策略或者獎勵條件顛倒的強化學習（upside-down RL）同等看待。未來更是可以將這些以結果為條件的 GFlowNets 擴展到隨機獎勵或隨機環境中。

此外，訓練一個以結果為條件的 GFlowNet 只能離線完成，因為條件輸入（如最終返回）可能只有在軌跡被采樣后才能知道。

論文的完整目錄如下：