經典動態規劃:0-1 背包問題
問題背景
月黑風高的夜晚,張三開啟了法外狂徒模式:他背著一個可裝載重量為 W 的背包去地主家偷東西。
地主家有 N 個物品,每個物品有重量和價值兩個屬性,其中第 i 個物品的重量為 wt[i],價值為 val[i]。
問張三現在用這個背包裝物品,最多能裝的價值是多少?
舉例:
- N = 3 //地主家有三樣東西
- wt = [2,1,3] //每樣東西的重量
- val = [4,2,3] //每樣東西的價值
- W = 4 //背包可裝載重量
算法應該返回 6.
因為選擇第一件物品和第二件物品,在重量沒有超出背包容量下,所選價值最大。
如果每種物品只能選 0 個或 1 個(即要么將此物品裝進包里要么不裝),則此問題稱為 0-1 背包問題;如果不限每種物品的數量,則稱為無界(或完全)背包問題。
今天這篇文章我們只關注 0-1 背包問題,下一篇文章再聊完全背包問題。
那我們是如何選擇要裝入的物品的?
思路初探
首先,質量很大價值很小的物品我們先不考慮(放著地主家金銀財寶珍珠首飾不偷,背出來一包煤...,那也就基本告別盜竊行業了...)
然后呢?再考慮質量大價值也大的?還是質量較小價值也稍小的?
我們自然而然想到:裝價值/質量 比值最大的,因為這至少能說明,此物品的“價質比”最大(也即貪心算法,每次選擇當前最優)
那么這樣裝能保證最后裝入背包里的價值最優嗎?
我們先來看一個例子:
假設有 5 個物品,N = 5,每種物品的質量與價值如下:
- W : 20, 30, 40, 50, 60
- V : 20, 30, 44, 55, 60
- V/W: 1, 1, 1.1, 1.1, 1
背包容量為 100
如果按上述策略:優先選“價質比”最大的:即第三個和第四個物品
- 此時質量:40+50=90
- 價值:44+55 =99
但我們知道,此題更優的選擇策略是:選第一個,第二個和第四個
- 此時質量:20+30+50=100
- 價值:20+30+55=105
所以,我們的“價質比”這種貪心策略顯然不是最優策略。
讀過一文學懂動態規劃這篇文章的讀者會發現,之前文章中兌換零錢例子我們最開始也是采取貪心策略,但最后發現貪心不是最優解,由此我們引出了動態規劃。
沒錯,今天這題也正是動態規劃又一經典的應用。
解題思路
根據動之前的文章我們知道,動態規劃的核心即:狀態與狀態轉移方程。
那么此題的狀態是什么呢?
狀態
何為狀態?
說白了,狀態就是已知條件。
重讀題意我們發現:此題的已知條件只有兩個:
- 背包容量
- 可選的物品
題目要求的是在滿足背包容量前提下,可裝入的最大價值。
那么我們可以根據上述狀態定義出 dp 數組,即:
dp[i][w] 表示:對于前i個物品,當前背包的容量為w,這種情況下可以裝的最大價值是dp[i][w]
我們自然而然的考慮到如下特殊情況:
當 i = 0 或 w = 0,那么:
dp[0][...] = dp[...][0] = 0
解釋:
對前 0 個物品而言,無論背包容量等于多少,裝入的價值為 0;
當背包容量為 0 時,無論裝入前多少個物品(因為一個都裝不進去),背包里的價值依舊為 0。
根據這個定義,我們求的最終答案就是dp[N][W]
我們現在找出了狀態,并找到了 base case,那么狀態之間該如何轉移呢(狀態轉移方程)?
狀態轉移方程
dp[i][w] 表示:對于前i個物品,當前背包的容量為w,這種情況下可以裝的最大價值是dp[i][w]。
思考:對于當前第 i 個物品:
- 如果沒有把第 i 個物品裝入包里(第 i 個物品質量大于當前背包容量):那么很顯然,最大價值dp[i][w]應該等于dp[i - 1][w],沒有裝進去嘛,故當前背包總價值就等于之前的結果,即第i - 1 個物品之前的總價值 。
- 如果把第 i 個物品裝入了包里,那么 dp[i][w]應該等于什么呢?
它應該等于下面兩者里的較大值:
- dp[i - 1][w] //前i - 1個物品,背包所裝的最大價值
- dp[i - 1]w - wt[i]] + val [i] //當前第 i 個物品我裝里邊了,那么此時背包裝入的總價值即為:當前第 i 個物品的價值 val [i] + 第 i 個物品之前,背包容量為w - wt[i](w 減去當前第 i 個物品的質量)dp[i - 1]w - wt[i]] 時的價值
上述兩個如果可以寫成以下代碼:
- //如果第i個物品質量大于當前背包容量
- if (wt[i] > W) {
- dp[i][W] = dp[i-1][W]; //繼承上一個結果
- } else {
- //在“上一個結果價值”和“把當前第i個物品裝入背包里所得到價值”二者里選價值較大的
- dp[i][W] = Math.max(dp[i-1][W],dp[i-1][W-wt[i]] + val[i])
- }
例子
我們接來下再用一個具體的例子,來理解狀態和狀態轉移方程。
現在我們有 4 個物品,物品對應的價值與質量分別如上圖左側所示:
- 6, 4
- 2,5
- 1, 4
- 8, 1
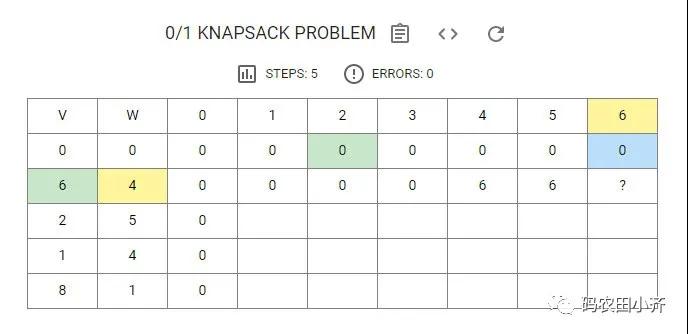
Step 1
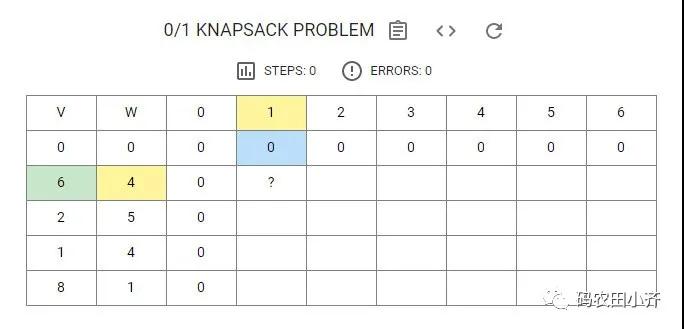
我們首先初始化一行和一列 0,分別對應dp[0][w] 和 dp[i][0]。
那么第一個問號處應該填什么呢?
我們根據上述表述的狀態轉移關系來判斷:
當前第一個物品的重量 4 > 背包容量,故裝不進去,所以繼承上一個結果。
上一個結果是什么呢?
就是第 i - 1個物品,也就是第 0 個,和W = 1時的價值:
- if (wt[i] > W) {
- dp[i][W] = dp[i-1][W]; //繼承上一個結果
- }
此時方框里的值為 0,故第一個問號這里應該填 0
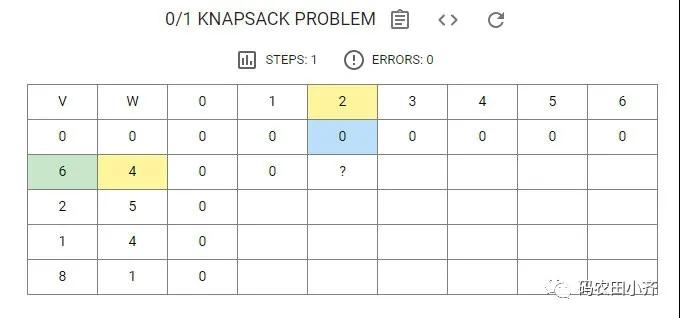
Step 2
現在我們走到了當背包容量 W = 2 的時候,此時當前 i (依舊第一個物品)能否裝進背包里呢?
我們發現 4 > 2,此時還是裝不進去,那么同樣繼承上一個結果。
上一個結果是 i 不變(依舊是第 **0 **個物品),W = 2,所以結果依舊為 0。
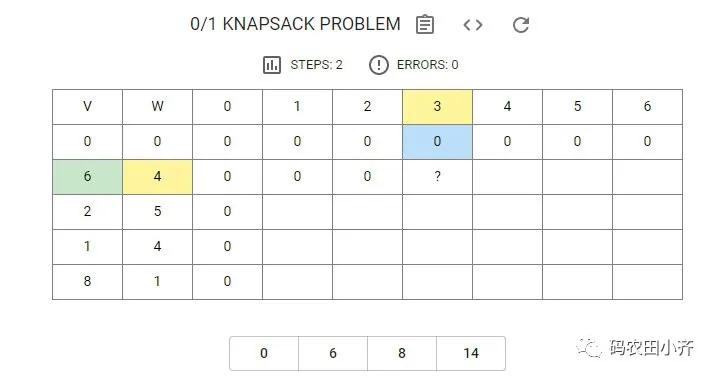
Step 3
現在來到 W = 3,發現依舊裝不進去,所以填 0。
Step 4
下一步到 W = 4 這里了,
此時物品重量 4 = 4(背包容量),可以裝里,那么按照之前狀態轉移關系應該是:
- else {
- //在“上一個結果價值”和“把當前第i個物品裝入背包里所得到價值”二者里選價值較大的
- dp[i][W] = Math.max(dp[i-1][W],dp[i-1][W-wt[i]] + val[i])
- }
Option A:
- 上一個結果 : dp[i - 1][w],即dp[0][4] = 0
Option B:
- 把當前第 i 個物品裝入背包里所得到價值:dp[i - 1]W - wt[i]] + val [i]
此時第一個物品的重量為 4,背包容量為 4,
故要想裝入重量為 4 的此物品,那么背包先前的容量必須為當前背包容量 - 當前物品容量:4 - 4 = 0。
我們隨即找到在沒裝入此物品(重量為 4,價值為 6)之前的dp[i -1]W - wt[i]] = dp[0][0] = 0
那么dp[i -1]W - wt[i]] + val [i] = 0 + 6 = 6
6 和 0 選擇一個最大值,所以這里問號處應填入6
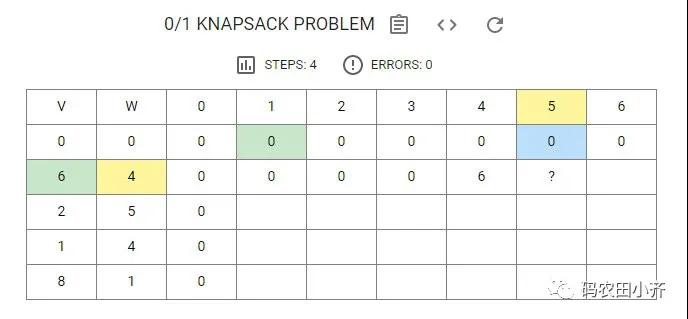
Step 5
下一步我們來到 W = 5 這里,此時依舊是第一個物品,質量 4 < 5(背包容量),我們可以裝里邊。
然后我們在
Option A:
- 上一個結果 :dp[0][5] = 0
Option B:
- 把當前第 i 個物品裝入背包里所得到價值:dp[i -1]W - wt[i]] + val [i]
此時第一個物品的重量為 4,背包容量為 5
故要想裝入重量為 4 的此物品,那么背包先前的容量必須為:當前背包容量 - 當前物品容量:5 - 4 = 1 ,
我們隨即找到在沒裝入此物品(重量為 4,價值為 6)之前的dp[i - 1]W - wt[i]] = dp[0][1] = 0
那么dp[i -1]W - wt[i]] + val [i] = 0 + 6 = 6
選擇一個最大值,即 6,所以此處應該填入 6
我們根據以上狀態轉系關系,依次可以填出空格其它值,最后我們得到整個 dp 數組:
| V | W | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 4 | 0 | 0 | 0 | 0 | 6 | 6 | 6 |
| 2 | 5 | 0 | 0 | 0 | 0 | 6 | 6 | 6 |
| 1 | 4 | 0 | 0 | 0 | 0 | 6 | 6 | 6 |
| 8 | 1 | 0 | 8 | 8 | 8 | 8 | 14 | 14 |
最后的 dp[4][6]:考慮前四個物品,背包容量為 6 的情況下,可裝入的最大價值,即為所求。
(注意:我們在這里求的是 0-1 背包問題,即某一個物品只能選擇 0 個或 1 個,不能多選!)
代碼
根據以上思路,我們很容易寫出代碼:
兩層 for 循環
外層循環 i 遍歷物品(即前幾個物品):
- for(int i = 1;i <=N;i++){
- ...
- }
內層循環 j 遍歷 1~W(背包容量)之間的整數值:
然后寫入狀態轉移方程
- for(int j = 0;j <= W;j++){
- //外層循環i,如果第i個物品質量大于當前背包容量
- if (wt[i] > W) {
- dp[i][W] = dp[i-1][W]; //繼承上一個結果
- } else {
- //在“上一個結果價值”和“把當前第i個物品裝入背包里所得到價值”二者里選價值較大的
- dp[i][W] = Math.max(dp[i-1][W],dp[i-1][W-wt[i]] + val[i])
- }
- }
由此我們給出完整代碼:
- class solution{
- public int knapsackProblem(int[] wt,int[] val,int size){
- //定義dp數組
- int[][] dp = new int[wt.length][size];
- //對于裝入前0個物品而言,dp數組儲存的總價值初始化為0
- for(int i = 0;i < size;i++){
- int[0][i] = 0;
- }
- //對于背包容量W=0時,裝入背包的總價值初始化為0
- for(int j = 0;j < size;j++){
- int[j][0] = 0;
- }
- //外層循環遍歷物品
- for(int i = 1;i <= N;i++){
- //內層循環遍歷1~W(背包容量)
- for(int j = 0;j <= W;j++){
- //外層循環i,如果第i個物品質量大于當前背包容量
- if (wt[i] > W) {
- dp[i][W] = dp[i-1][W]; //繼承上一個結果
- } else {
- //在“上一個結果價值”和“把當前第i個物品裝入背包里所得到價值”二者里選價值較大的
- dp[i][W] = Math.max(dp[i-1][W],dp[i-1][W-wt[i]] + val[i])
- }
- }
- }
- }
- }
只要我們定義好了狀態(dp 數組的定義),理清了狀態之間是如何轉移的,最后的代碼水到渠成。
本文所說的這個 0-1 背包問題,Leetcode 上并沒有這個原題,所以對于背包問題,最重要的是它的變種。
背包問題是一大類問題的統稱,很大一部分動態規劃的題深層剖析都可以轉換為背包問題。
所以還需要理解體會背包問題的核心思想,再將此種思想運用到其它一類背包問題的問題上。
那么背包問題還有哪些變化呢?我們下期見~