[[376845]]

對于面試的話，其實掌握01背包，和完全背包，就夠用了，最多可以再來一個多重背包。

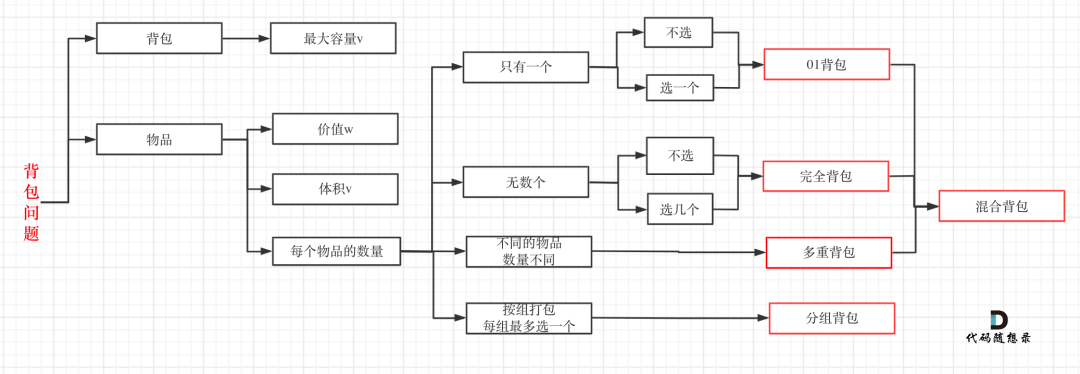
如果這幾種背包，分不清，我這里畫了一個圖，如下：

至于背包九講其其他背包，面試幾乎不會問，都是競賽級別的了，leetcode上連多重背包的題目都沒有，所以題庫也告訴我們，01背包和完全背包就夠用了。

而完全背包又是也是01背包稍作變化而來，即：完全背包的物品數(shù)量是無限的。

所以背包問題的理論基礎(chǔ)重中之重是01背包，一定要理解透!

leetcode上沒有純01背包的問題，都是01背包應(yīng)用方面的題目，也就是需要轉(zhuǎn)化為01背包問題。

所以我先通過純01背包問題，把01背包原理講清楚，后續(xù)再講解leetcode題目的時候，重點就是講解如何轉(zhuǎn)化為01背包問題了。

之前可能有些錄友已經(jīng)可以熟練寫出背包了，但只要把這個文章仔細看完，相信你會意外收獲!

01 背包

有N件物品和一個最多能被重量為W 的背包。第i件物品的重量是weight[i]，得到的價值是value[i] 。每件物品只能用一次，求解將哪些物品裝入背包里物品價值總和最大。

[[376846]]

這是標(biāo)準(zhǔn)的背包問題，以至于很多同學(xué)看了這個自然就會想到背包，甚至都不知道暴力的解法應(yīng)該怎么解了。

這樣其實是沒有從底向上去思考，而是習(xí)慣性想到了背包，那么暴力的解法應(yīng)該是怎么樣的呢?

每一件物品其實只有兩個狀態(tài)，取或者不取，所以可以使用回溯法搜索出所有的情況，那么時間復(fù)雜度就是O(2^n)，這里的n表示物品數(shù)量。

所以暴力的解法是指數(shù)級別的時間復(fù)雜度。進而才需要動態(tài)規(guī)劃的解法來進行優(yōu)化!

在下面的講解中，我舉一個例子：

背包最大重量為4。

物品為：

	重量	價值
物品0	1	15
物品1	3	20
物品2	4	30

問背包能背的物品最大價值是多少?

以下講解和圖示中出現(xiàn)的數(shù)字都是以這個例子為例。

二維dp數(shù)組01背包

依然動規(guī)五部曲分析一波。

確定dp數(shù)組以及下標(biāo)的含義

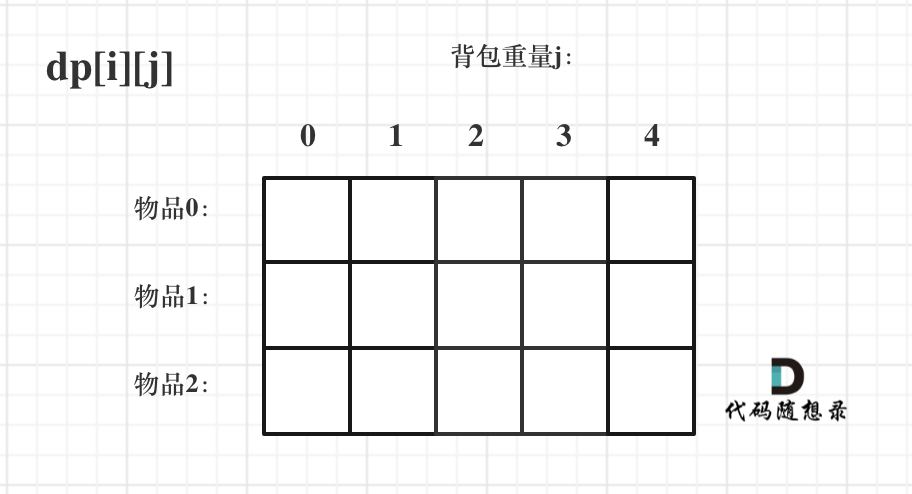
對于背包問題，有一種寫法， 是使用二維數(shù)組，即dp[i][j] 表示從下標(biāo)為[0-i]的物品里任意取，放進容量為j的背包，價值總和最大是多少。

只看這個二維數(shù)組的定義，大家一定會有點懵，看下面這個圖：

要時刻記著這個dp數(shù)組的含義，下面的一些步驟都圍繞這dp數(shù)組的含義進行的，如果哪里看懵了，就來回顧一下i代表什么，j又代表什么。

2.確定遞推公式

再回顧一下dp[i][j]的含義：從下標(biāo)為[0-i]的物品里任意取，放進容量為j的背包，價值總和最大是多少。

那么可以有兩個方向推出來dp[i][j]，

• 由dp[i - 1][j]推出，即背包容量為j，里面不放物品i的最大價值，此時dp[i][j]就是dp[i - 1][j]
• 由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 為背包容量為j - weight[i]的時候不放物品i的最大價值，那么dp[i - 1][j - weight[i]] + value[i] (物品i的價值)，就是背包放物品i得到的最大價值

所以遞歸公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3.dp數(shù)組如何初始化

關(guān)于初始化，一定要和dp數(shù)組的定義吻合，否則到遞推公式的時候就會越來越亂。

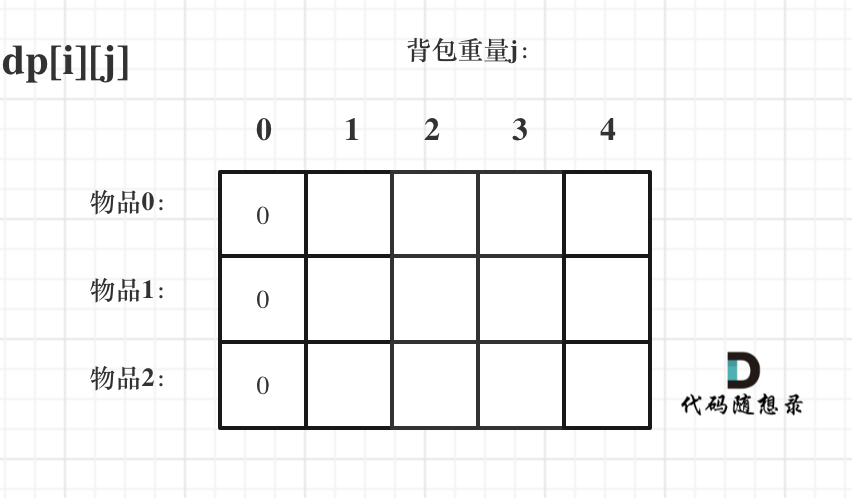
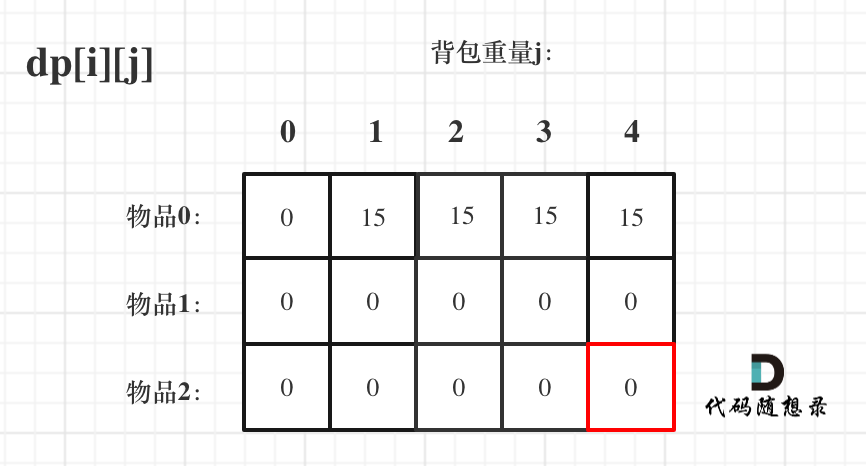
首先從dp[i][j]的定義觸發(fā)，如果背包容量j為0的話，即dp[i][0]，無論是選取哪些物品，背包價值總和一定為0。如圖：

再看其他情況。

狀態(tài)轉(zhuǎn)移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推導(dǎo)出來，那么i為0的時候就一定要初始化。

dp[0][j]，即：i為0，存放編號0的物品的時候，各個容量的背包所能存放的最大價值。

代碼如下：

// 倒敘遍歷 
for (int j = bagWeight; j >= weight[0]; j--) { 
    dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i為0時候的情況 
} 

大家應(yīng)該發(fā)現(xiàn)，這個初始化為什么是倒敘的遍歷的?正序遍歷就不行么?

正序遍歷還真就不行，dp[0][j]表示容量為j的背包存放物品0時候的最大價值，物品0的價值就是15，因為題目中說了**每個物品只有一個!**所以dp[0][j]如果不是初始值的話，就應(yīng)該都是物品0的價值，也就是15。

但如果一旦正序遍歷了，那么物品0就會被重復(fù)加入多次!例如代碼如下：

// 正序遍歷 
for (int j = weight[0]; j <= bagWeight; j++) { 
    dp[0][j] = dp[0][j - weight[0]] + value[0]; 
} 

例如dp[0][1] 是15，到了dp[0][2] = dp[0][2 - 1] + 15; 也就是dp[0][2] = 30 了，那么就是物品0被重復(fù)放入了。

所以一定要倒敘遍歷，保證物品0只被放入一次!這一點對01背包很重要，后面在講解滾動數(shù)組的時候，還會用到倒敘遍歷來保證物品使用一次!

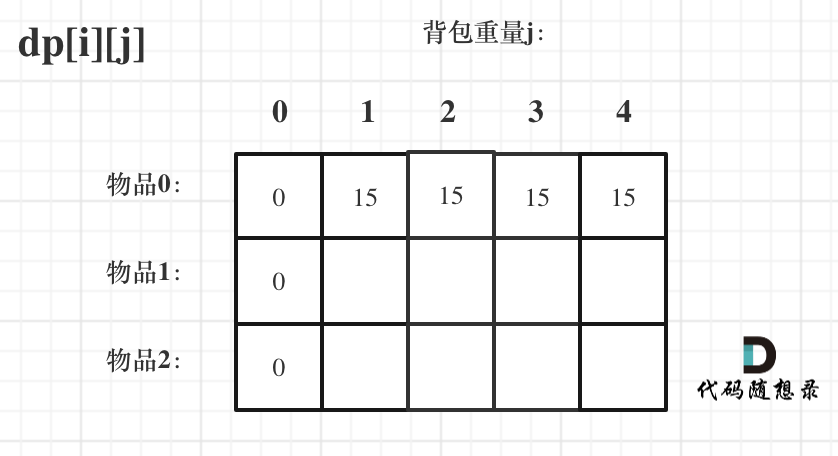
此時dp數(shù)組初始化情況如圖所示：

dp[0][j] 和 dp[i][0] 都已經(jīng)初始化了，那么其他下標(biāo)應(yīng)該初始化多少呢?

dp[i][j]在推導(dǎo)的時候一定是取價值最大的數(shù)，如果題目給的價值都是正整數(shù)那么非0下標(biāo)都初始化為0就可以了，因為0就是最小的了，不會影響取最大價值的結(jié)果。

如果題目給的價值有負數(shù)，那么非0下標(biāo)就要初始化為負無窮了。例如：一個物品的價值是-2，但對應(yīng)的位置依然初始化為0，那么取最大值的時候，就會取0而不是-2了，所以要初始化為負無窮。

這樣才能讓dp數(shù)組在遞歸公式的過程中取最大的價值，而不是被初始值覆蓋了。

最后初始化代碼如下：

// 初始化 dp 
vector<vector<int>> dp(weight.size() + 1, vector<int>(bagWeight + 1, 0)); 
for (int j = bagWeight; j >= weight[0]; j--) { 
    dp[0][j] = dp[0][j - weight[0]] + value[0]; 
} 

費了這么大的功夫，才把如何初始化講清楚，相信不少同學(xué)平時初始化dp數(shù)組是憑感覺來的，但有時候感覺是不靠譜的。

4.確定遍歷順序

在如下圖中，可以看出，有兩個遍歷的維度：物品與背包重量

那么問題來了，先遍歷 物品還是先遍歷背包重量呢?

其實都可以!!但是先遍歷物品更好理解。

那么我先給出先遍歷物品，然后遍歷背包重量的代碼。

// weight數(shù)組的大小 就是物品個數(shù) 
for(int i = 1; i < weight.size(); i++) { // 遍歷物品 
    for(int j = 0; j <= bagWeight; j++) { // 遍歷背包容量  
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 這個是為了展現(xiàn)dp數(shù)組里元素的變化 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 
         
    } 
} 

先遍歷背包，再遍歷物品，也是可以的!(注意我這里使用的二維dp數(shù)組)

例如這樣：

// weight數(shù)組的大小 就是物品個數(shù) 
for(int j = 0; j <= bagWeight; j++) { // 遍歷背包容量 
    for(int i = 1; i < weight.size(); i++) { // 遍歷物品 
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 
    } 
} 

為什么也是可以的呢?

要理解遞歸的本質(zhì)和遞推的方向。

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 遞歸公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推導(dǎo)出來的。

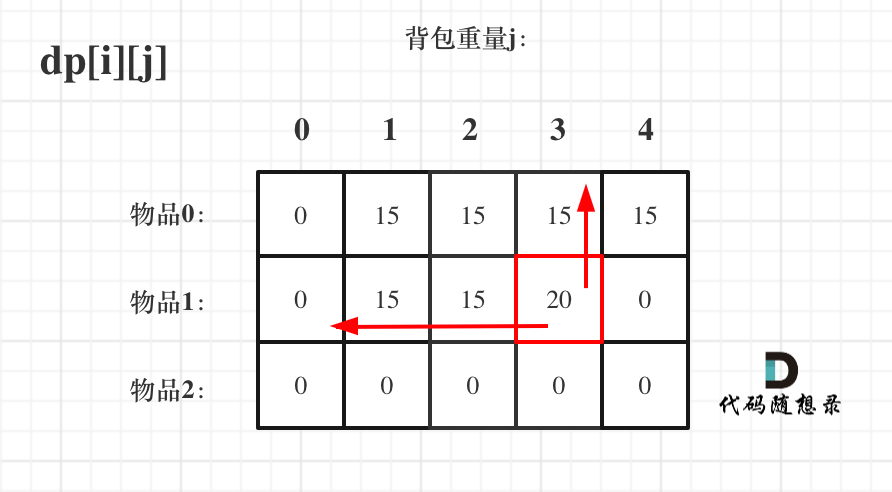
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正左和正上兩個方向)，那么先遍歷物品，再遍歷背包的過程如圖所示：

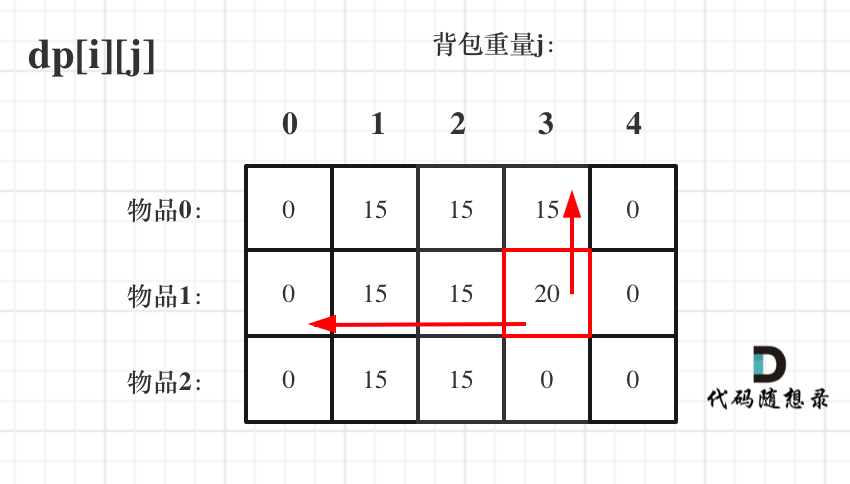
再來看看先遍歷背包，再遍歷物品呢，如圖：

大家可以看出，雖然兩個for循環(huán)遍歷的次序不同，但是dp[i][j]所需要的數(shù)據(jù)就是左上角，根本不影響dp[i][j]公式的推導(dǎo)!

但先遍歷物品再遍歷背包這個順序更好理解。

其實背包問題里，兩個for循環(huán)的先后循序是非常有講究的，理解遍歷順序其實比理解推導(dǎo)公式難多了。

5.舉例推導(dǎo)dp數(shù)組

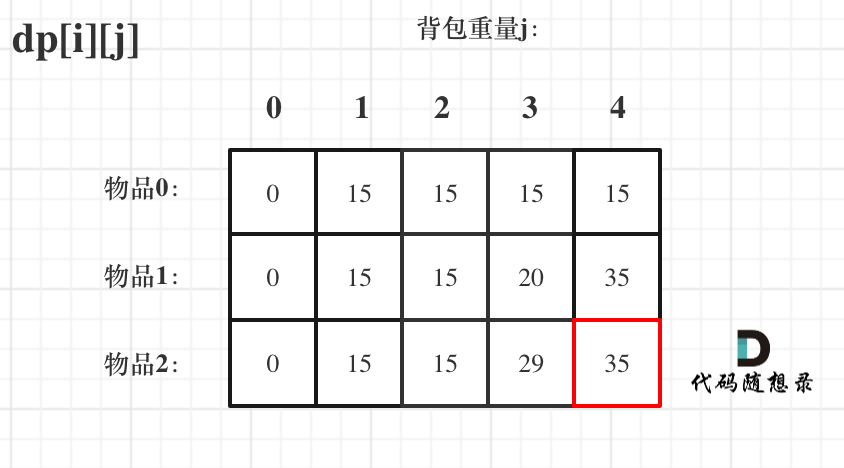
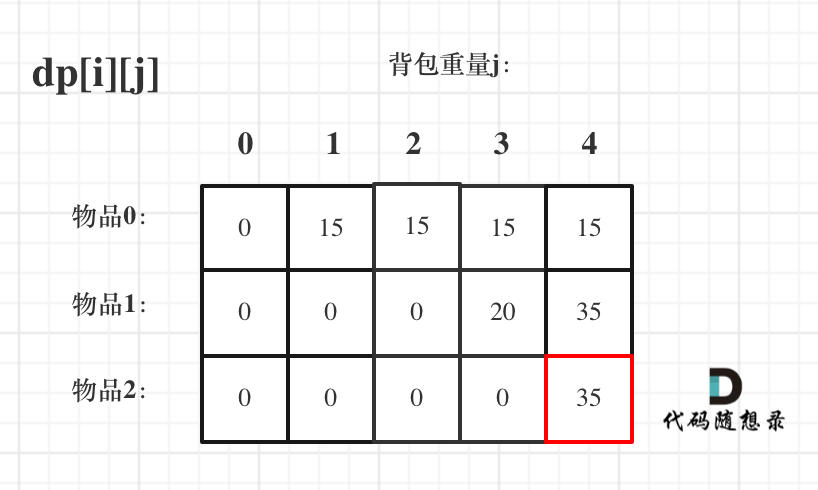
來看一下對應(yīng)的dp數(shù)組的數(shù)值，如圖：

最終結(jié)果就是dp[2][4]。

建議大家此時自己在紙上推導(dǎo)一遍，看看dp數(shù)組里每一個數(shù)值是不是這樣的。

做動態(tài)規(guī)劃的題目，最好的過程就是自己在紙上舉一個例子把對應(yīng)的dp數(shù)組的數(shù)值推導(dǎo)一下，然后在動手寫代碼!

很多同學(xué)做dp題目，遇到各種問題，然后憑感覺東改改西改改，怎么改都不對，或者稀里糊涂就改過了。

主要就是自己沒有動手推導(dǎo)一下dp數(shù)組的演變過程，如果推導(dǎo)明白了，代碼寫出來就算有問題，只要把dp數(shù)組打印出來，對比一下和自己推導(dǎo)的有什么差異，很快就可以發(fā)現(xiàn)問題了。

完整C++測試代碼

void test_2_wei_bag_problem1() { 
    vector<int> weight = {1, 3, 4}; 
    vector<int> value = {15, 20, 30}; 
    int bagWeight = 4; 
 
    // 二維數(shù)組 
    vector<vector<int>> dp(weight.size() + 1, vector<int>(bagWeight + 1, 0)); 
 
    // 初始化  
    for (int j = bagWeight; j >= weight[0]; j--) { 
        dp[0][j] = dp[0][j - weight[0]] + value[0]; 
    } 
 
    // weight數(shù)組的大小 就是物品個數(shù) 
    for(int i = 1; i < weight.size(); i++) { // 遍歷物品 
        for(int j = 0; j <= bagWeight; j++) { // 遍歷背包容量 
            if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 
 
        } 
    } 
 
    cout << dp[weight.size() - 1][bagWeight] << endl; 
} 
 
int main() { 
    test_2_wei_bag_problem1(); 
} 

以上遍歷的過程也可以這么寫：

// 遍歷過程 
for(int i = 1; i < weight.size(); i++) { // 遍歷物品 
    for(int j = 0; j <= bagWeight; j++) { // 遍歷背包容量 
        if (j - weight[i] >= 0) { 
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 
        } 
    } 
} 

這么寫打印出來的dp數(shù)據(jù)這就是這樣：

空出來的0其實是用不上的，版本一 能把完整的dp數(shù)組打印出來，出來我用版本一來講解。

總結(jié)

講了這么多才剛剛把二維dp的01背包講完，這里大家其實可以發(fā)現(xiàn)最簡單的是推導(dǎo)公式了，推導(dǎo)公式估計看一遍就記下來了，但難就難在如何初始化和遍歷順序上。

可能有的同學(xué)并沒有注意到初始化 和 遍歷順序的重要性，我們后面做力扣上背包面試題目的時候，大家就會感受出來了。

本文轉(zhuǎn)載自微信公眾號「 代碼隨想錄」，可以通過以下二維碼關(guān)注。轉(zhuǎn)載本文請聯(lián)系代碼隨想錄公眾號。