[[431832]]

前言

大家好，我是bigsai，好久不見，甚是想念(天天想念)!

很久前就有小伙伴被動態規劃所折磨，確實，很多題動態規劃確實太難看出了了，甚至有的題看了題解理解起來都費勁半天。

動態規劃的范圍雖然確實是很廣很難，但是從整個動態規劃出現的頻率來看，這幾種基礎的動態規劃理解容易，學習起來壓力不大，并且出現頻率非常高。

這幾個常見的動態規劃有：連續子數組最大和，子數組的最大乘積，最長遞增子序列(LIS)，最長公共子序列(LCS)，最長公共子串，最長公共子串，不同子序列。

什么是動態規劃

首先很多人問，何為動態規劃?動態規劃(Dynamic Programming，DP)是運籌學的一個分支，是求解決策過程最優化的過程。通俗一點動態規劃就是從下往上(從前向后)階梯型求解數值。

那么動態規劃和遞歸有什么區別和聯系?

總的來說動態規劃從前向后，遞歸從后向前，兩者策略不同，并且一般動態規劃效率高于遞歸。

不過都要考慮初始狀態，上下層數據之間的聯系。很多時候用動態規劃能解決的問題，用遞歸也能解決不過很多時候效率不高可能會用到記憶化搜索。

不太明白?

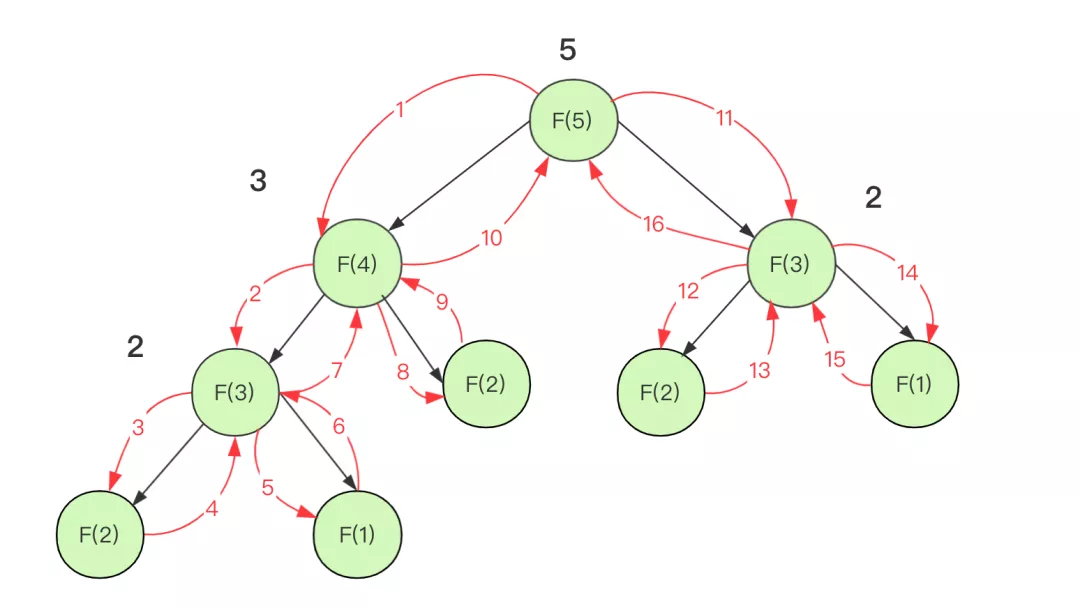
就拿求解斐波那契額數列來說，如果直接用遞歸不優化，那么復雜度太多會進行很多重復的計算。

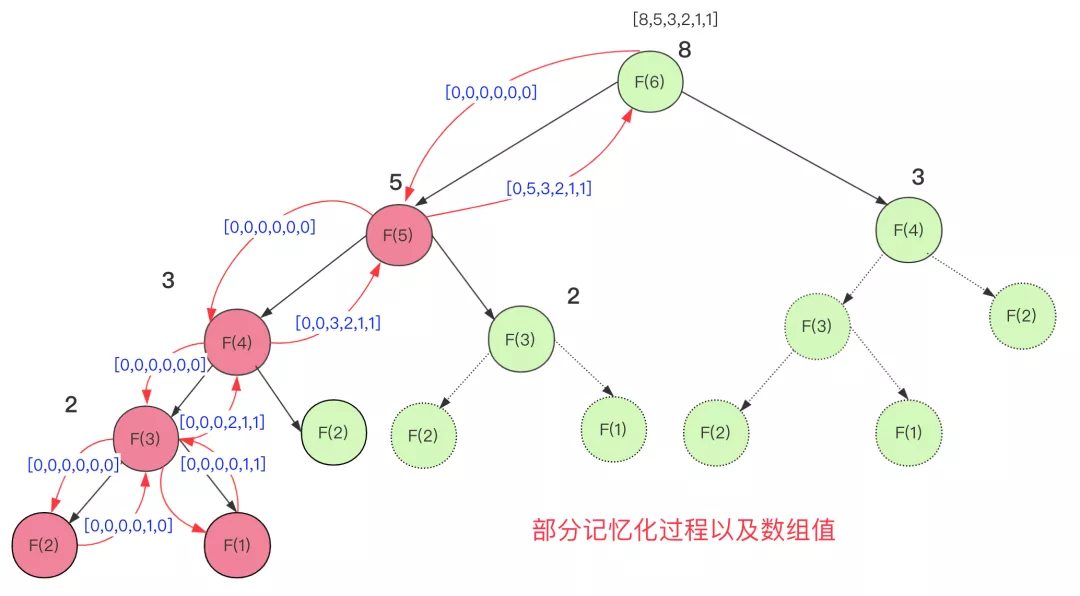
但是利用記憶化你可以理解為一層緩存，將求過的值存下來下次再遇到就直接使用就可以了。

實現記憶化搜索求斐波那契代碼為：

static long F(int n,long record[]) 
{ 
  if(n==1||n==2) {return 1;} 
  if(record[n]>0) 
    return record[n]; 
  else 
    record[n]=F(n-1,record)+F(n-2,record); 
  return record[n]; 
} 
public static void main(String[] args) { 
  int n=6; 
  long[] record = new long[n+1]; 
  System.out.println(F(n,record)); 
} 

而動態規劃的方式你可以從前往后邏輯處理，從第三個開始每個dp都是前兩個dp之和。

public int fib(int n) { 
       int dp[]=new int[n+1]; 
       dp[0]=0; 
       dp[1]=1; 
       for(int i=2;i<n+1;i++){ 
           dp[i]=dp[i-1]+dp[i-2]; 
       } 
       return dp[n]; 
   } 

當然動態規劃也能有很多空間優化，有些只用一次的值，你可以用一些變量去替代。有些二維數組很大也可以用一維數組交替替代。當然動態規劃專題很大，有很多比如樹形dp、狀壓dp、背包問題等等經常出現在競賽中，能力有限這里就將一些出現筆試高頻的動態規劃!

連續子數組最大和

給定一個整數數組 nums ，找到一個具有最大和的連續子數組(子數組最少包含一個元素)，返回其最大和。

示例:

輸入: [-2,1,-3,4,-1,2,1,-5,4] 
輸出: 6 
解釋: 連續子數組 [4,-1,2,1] 的和最大，為 6。 

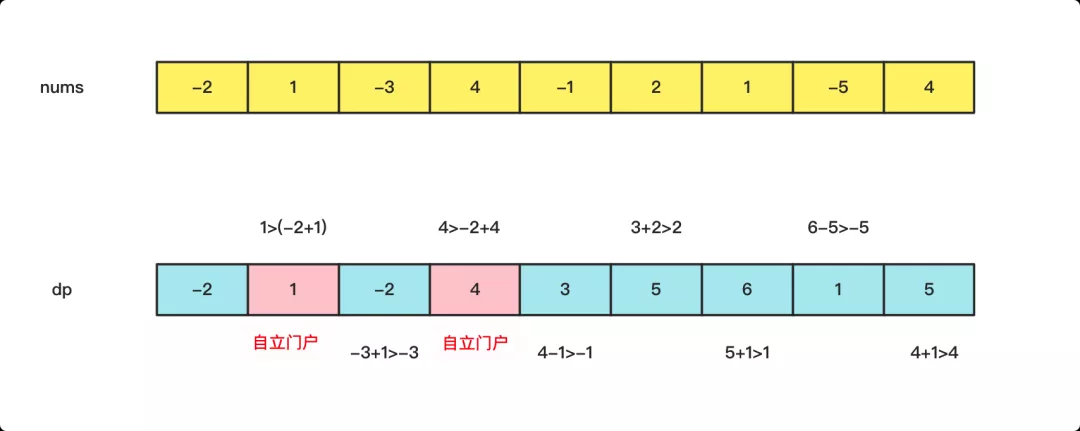
 dp的方法就是O(n)的方法。如果dp[i]表示以第i個結尾的最大序列和，而這個dp的狀態方程為：

dp[0]=a[0] 
dp[i]=max(dp[i-1]+a[i],a[i]) 

也不難解釋，如果以前一個為截至的最大子序列和大于0，那么就連接本個元素，否則本個元素就自立門戶。 

實現代碼為：

public int maxSubArray(int[] nums) { 
    int dp[]=new int[nums.length]; 
    int max=nums[0]; 
    dp[0]=nums[0]; 
    for(int i=1;i<nums.length;i++) 
    { 
      dp[i]=Math.max(dp[i-1]+nums[i],nums[i]); 
      if(dp[i]>max) 
        max=dp[i]; 
    } 
    return max; 
} 

ps:有小伙伴問那求可以不連續的數組最大和呢?你好好想想枚舉一下正的收入囊中，那個問題沒意義的。

連續子數組最大乘積

給你一個整數數組 nums ，請你找出數組中乘積最大的連續子數組(該子數組中至少包含一個數字)，并返回該子數組所對應的乘積。

示例 :

輸入: [2,3,-2,4] 
輸出: 6 
解釋: 子數組 [2,3] 有最大乘積 6。 

連續子數組的最大乘積，這也是一道經典的動態規劃問題，但是和普通動態規劃又有點小不同。

如果數據中都是非負數，對于連續數組的最大乘積，那樣處理起來和前面連續子數組最大和處理起來有些相似，要么和前面的疊乘，要么自立門戶。

dp[0]=nums[0] 
dp[i]=max(dp[i-1]*a[i],a[i]) 

但是這里面的數據會出現負數，乘以一個負數它可能從最大變成最小，并且還有負負得正就又可能變成最大了。

這時候該怎么考慮呢?

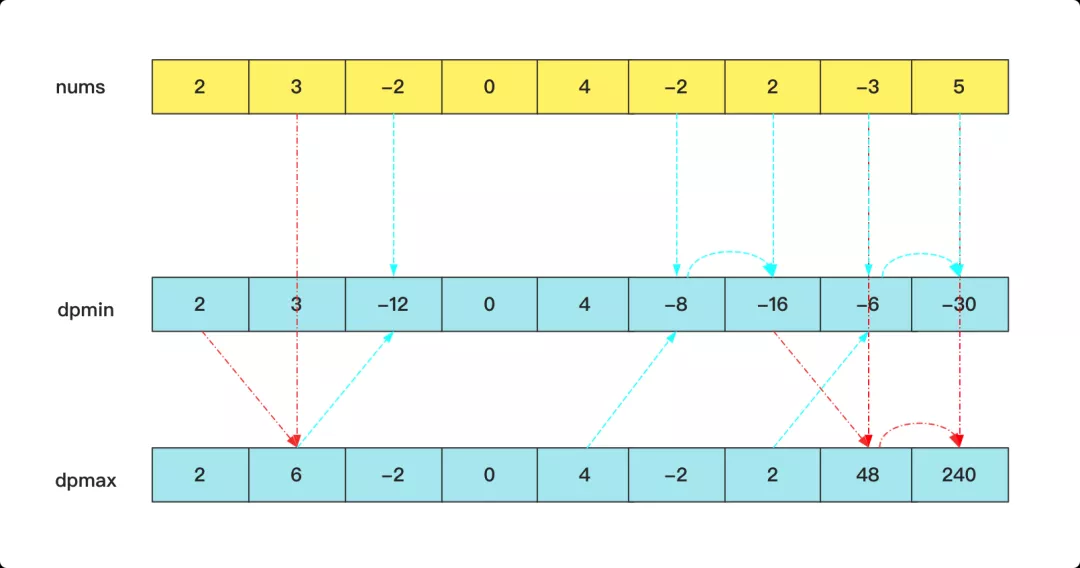
容易，我們開兩個dp，一個dpmax[]記錄乘積的最大值，一個dpmin[]記錄乘積的最小值。然后每次都更新dpmax和dpmin不管當前值是正數還是負數.這樣通過這兩個數組就可以記錄乘積的絕對值最大。

動態方程也很容易

dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i]) 
dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i]) 

看一個過程就能理解明白，dpmin就是起到中間過度的作用，記錄一些可能的負極值以防備用。結果還是dpmax中的值。

最長遞增子序列

最長遞增子序列，也稱為LIS,是出現非常高頻的動態規劃算法之一。這里對應力扣300

給你一個整數數組 nums ，找到其中最長嚴格遞增子序列的長度。

子序列是由數組派生而來的序列，刪除(或不刪除)數組中的元素而不改變其余元素的順序。例如，[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列。

輸入：nums = [0,1,0,3,2,3] 
輸出：4 
解釋：最長遞增子序列是 [0,1,2,3]，因此長度為 4 。 

對于最長遞增子序列，如果不考慮動態規劃的方法，使用暴力枚舉其實還是比較麻煩的，因為你不知道遇到比前面元素大的是否要遞增。

比如 1 10 3 11 4 5，這個序列不能選取1 10 11而1 3 4 5才是最大的，所以暴力枚舉所有情況的時間復雜度還是非常高的。

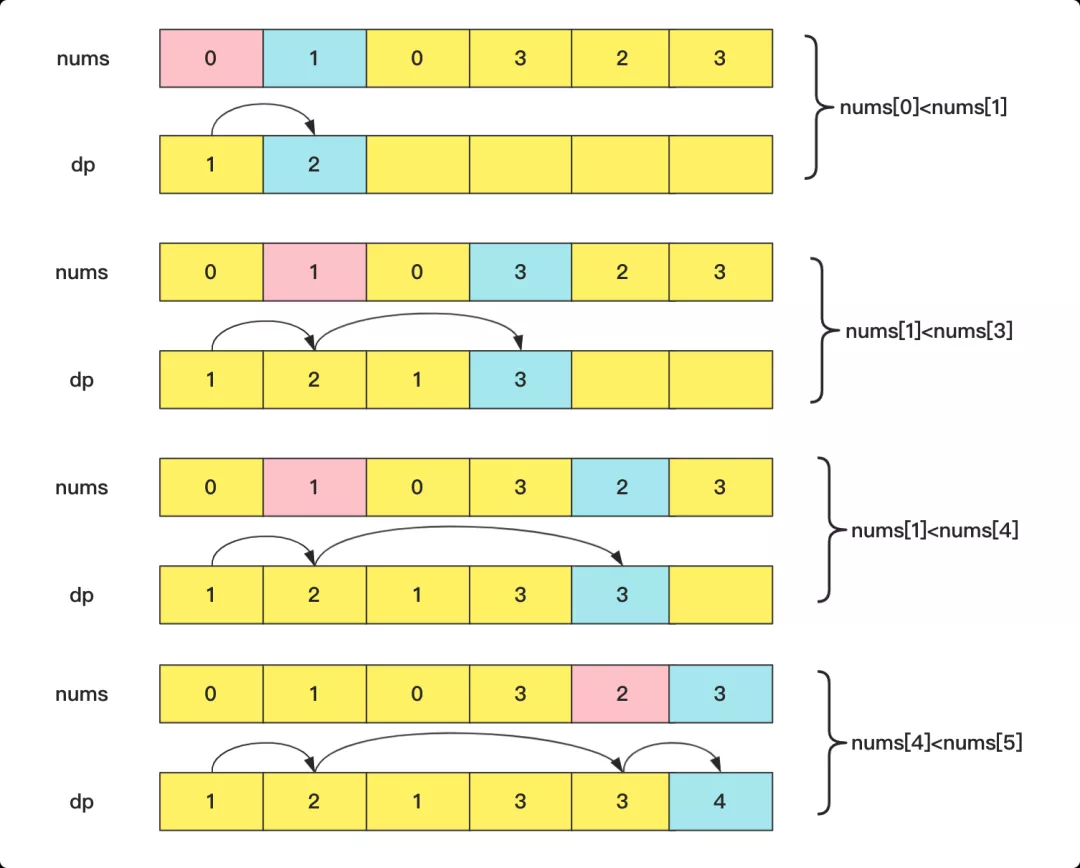
如果我們采取動態規劃的方法，創建的dp[]數組，dp[i]表示以nums[i]結尾的最長遞增子序列，而dp[i]的求解方式就是枚舉i號前面的元素和對應結尾的最長子序列，找到一個元素值小于nums[i]并且遞增序列最長，這樣的時間復雜度為O(n2)。

狀態轉移方程為：

dp[i]=max(dp[j])+1, 其中0≤j<i且num[j]<num[i] 

具體流程為：

實現代碼為：

class Solution { 
    public int lengthOfLIS(int[] nums) { 
        int dp[]=new int[nums.length]; 
        int maxLen=1; 
        dp[0]=1; 
        for(int i=1;i<nums.length;i++){ 
            int max=0;//統計前面 末尾數字比自己小 最長遞增子串 
            for(int j=0;j<i;j++){//枚舉 
                //結尾數字小于當前數字 并且長度大于記錄的最長 
                if(nums[j]<nums[i]&&dp[j]>max){ 
                    max=dp[j]; 
                } 
            } 
            dp[i]=max+1;//前面最長 加上自己 
            if(maxLen<dp[i]) 
                maxLen=dp[i]; 
        } 
        return maxLen; 
    } 
} 

不過這道題還有一個優化，可以優化成O(nlogn)的時間復雜度。

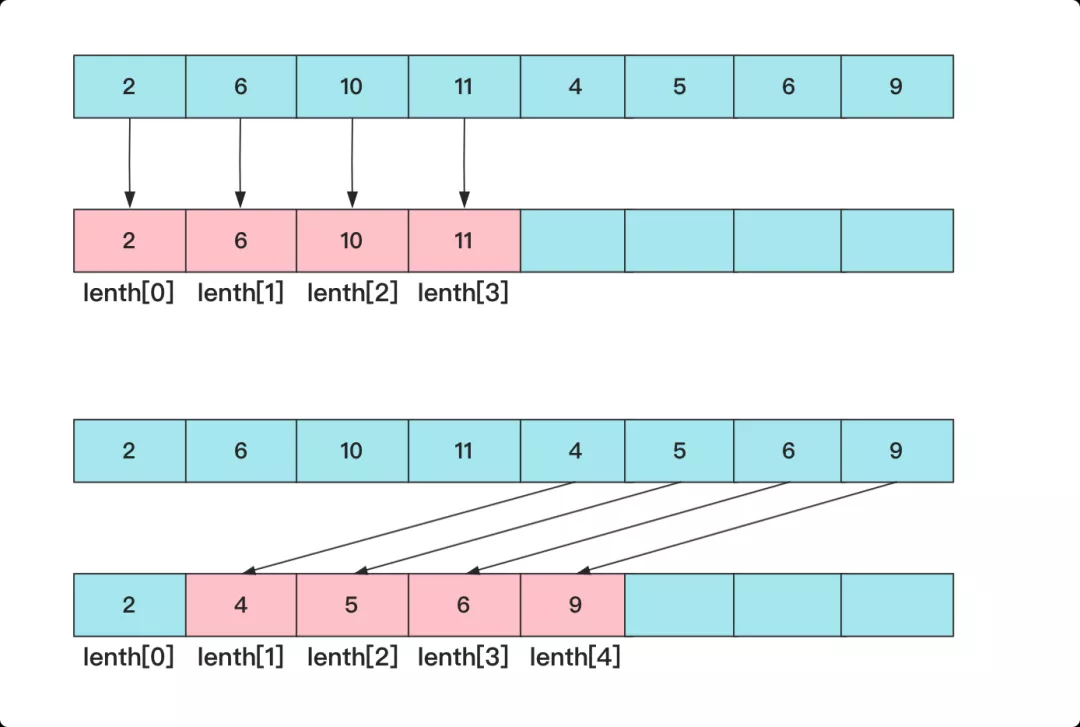
我們用dp記錄以 nums[i] 結尾的最長子序列長度,縱觀全局，我們希望在長度一致的情況下末尾的值能夠盡量的小!

例如 2,3,9,5 …… 在前面最長的長度為3 我們愿意拋棄2,3,9 而全部使用2,3,5 。也就是對于一個值，我們希望這個值能更新以它為結尾的最長的序列的末尾值。

如果這個值更新不了最長的序列，那就嘗試更新第二長的末尾值以防待用。例如 2,3,9,5,4,5 這個序列2,3,5更新2,3,9;然后2,3,4更新2,3,5 為最長的2,3,4,5做鋪墊。

而這個思路的核心就是維護一個lenth[]數組，length[i]表示長度為i的子序列末尾最小值，因為我們每次順序增加一個長度說明這個值比前面的都大(做了充分比較)，所以這個數組也是個遞增的，遞增，那么在鎖定位置更新最大長度序列尾值的時候可以使用二分法優化。

實現代碼為：

class Solution { 
    public int lengthOfLIS(int[] nums) { 
        int length[]=new int[nums.length]; 
        int len=1; 
        length[0]=nums[0]; 
        for(int i=1;i<nums.length;i++){ 
            int left=0,right=len; 
            while (left<right){ 
                int mid=left+(right-left)/2; 
                if(length[mid]<nums[i]){ 
                    left=mid+1; 
                }else { 
                    right=mid; 
                } 
            } 
            length[left]=nums[i]; 
            if(right==len) 
                len++;         
        } 
        return len; 
    } 
} 

最長公共子序列

最長公共子序列也成為LCS.出現頻率非常高!

給定兩個字符串 text1 和 text2，返回這兩個字符串的最長 公共子序列 的長度。如果不存在 公共子序列 ，返回 0 。

一個字符串的 子序列 是指這樣一個新的字符串：它是由原字符串在不改變字符的相對順序的情況下刪除某些字符(也可以不刪除任何字符)后組成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

兩個字符串的 公共子序列 是這兩個字符串所共同擁有的子序列。

拿b c d d e和 a c e e d e舉例，其的公共子串為c d e。如果使用暴力，復雜度太高會直接超時，就需要使用動態規劃。兩個字符串匹配，我們設立二維dp[][]數組，dp[i][j]表示text1串第i個結尾，text2串第j個結尾的最長公共子串的長度。

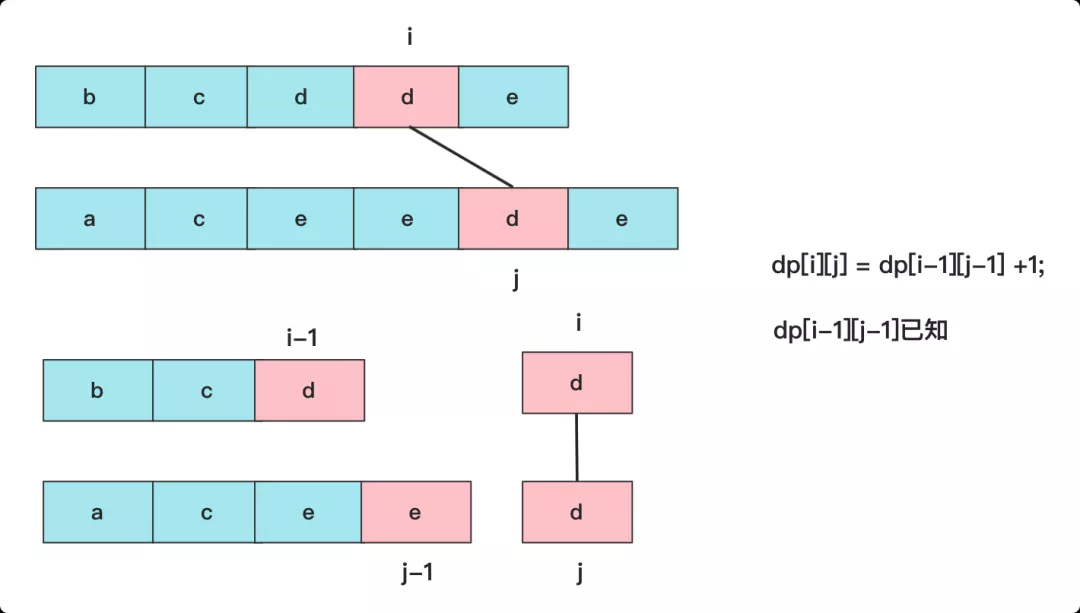
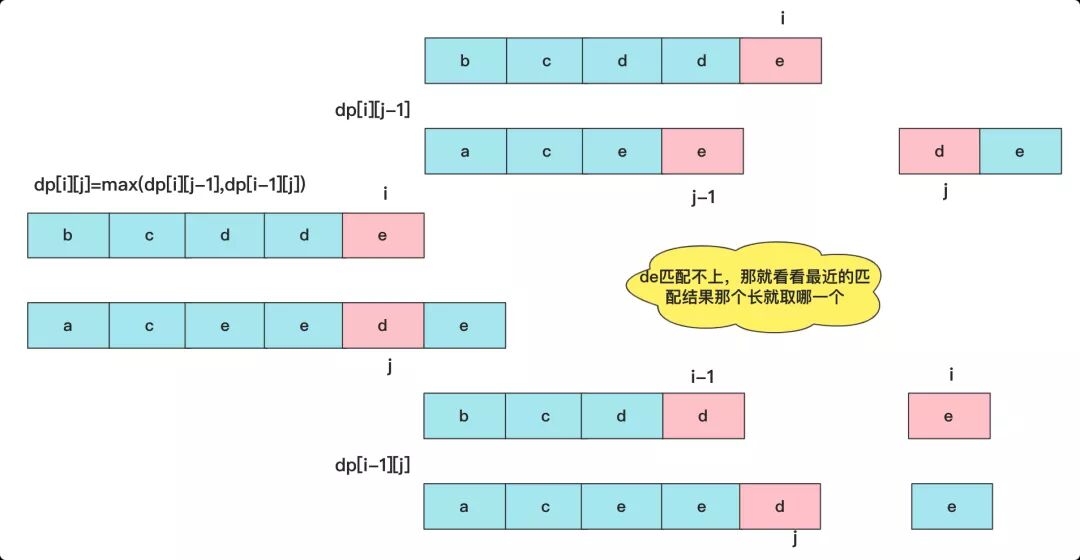
這里核心就是要搞懂狀態轉移，分析dp[i][j]的轉換情況，當到達i,j時候：

如果text1[i]==text2[j],因為兩個元素都在最末尾的位置，所以一定可以匹配成功，換句話說，這個位置的鄰居dp值不可能大于他(最多相等)。所以這個時候就是dp[i][j]=dp[i-1][j-1] +1;

如果text1[i]!=text2[j]，就有兩種可能性，我們知道的鄰居有dp[i-1][j],dp[i][j-1]，很多人還會想到dp[i-1][j-1]這個一定比前兩個小于等于，因為就是前面兩個子范圍嘛!所以這時就相當于末尾匹配不成，就要看看鄰居能匹配的最大值啦，此時dp[i][j]=max(dp[i][j-1],dp[i-1][j])。

所以整個狀態轉移方程為：

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]時 
dp[i][j] = max(dp[i][j-1],dp[i-1][j])  //text1[i]!=text2[j]時 

實現代碼為：

class Solution { 
    public int longestCommonSubsequence(String text1, String text2) { 
        char ch1[]=text1.toCharArray(); 
        char ch2[]=text2.toCharArray(); 
        int dp[][]=new int[ch1.length+1][ch2.length+1]; 
        for(int i=0;i<ch1.length;i++) 
        { 
            for(int j=0;j<ch2.length;j++) 
            { 
                if(ch1[i]==ch2[j]) 
                { 
                    dp[i+1][j+1]=dp[i][j]+1; 
                } 
                else 
                    dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j]); 
 
            } 
        } 
        return dp[ch1.length][ch2.length]; 
    } 
} 

最長公共子串

給定兩個字符串str1和str2,輸出兩個字符串的最長公共子串。

例如 abceef 和a2b2cee3f的最長公共子串就是cee。公共子串是兩個串中最長連續的相同部分。

如何分析呢? 和上面最長公共子序列的分析方式相似，要進行動態規劃匹配，并且邏輯上處理更簡單，只要當前i,j不匹配那么dp值就為0，如果可以匹配那么就變成dp[i-1][j-1] + 1

核心的狀態轉移方程為：

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]時 
dp[i][j] = 0  //text1[i]!=text2[j]時 

這里代碼和上面很相似就不寫啦，但是有個問題有的會讓你輸出最長字符串之類，你要記得用一些變量存儲值。

不同子序列

不同子序列也會出現，并且有些難度，前面這篇不同子序列問題分析講的大家可以看看。

給定一個字符串 s 和一個字符串 t ，計算在 s 的子序列中 t 出現的個數。

字符串的一個 子序列 是指，通過刪除一些(也可以不刪除)字符且不干擾剩余字符相對位置所組成的新字符串。(例如，"ACE" 是 "ABCDE" 的一個子序列，而 "AEC" 不是)

示例 ：

輸入：s = "rabbbit", t = "rabbit" 
輸出：3 
解釋： 
如下圖所示, 有 3 種可以從 s 中得到 "rabbit" 的方案。 
(上箭頭符號 ^ 表示選取的字母) 
rabbbit 
^^^^ ^^ 
rabbbit 
^^ ^^^^ 
rabbbit 
^^^ ^^^ 

分析：

這個問題其實就是上面有幾個pat的變形拓展，其基本思想其實是一致的，上面那題問的是有幾個pat，固定、且很短。但這里面t串的長度不固定，所以處理上就要使用數組來處理而不能直接if else。

這題的思路肯定也是動態規劃dp了，dp[j]的意思就是t串中[0,j-1]長字符在s中能夠匹配的數量(當然這個值從前往后是動態變化的)，數組大小為dp[t.length+1]。在遍歷s串的每一個元素都要和t串中所有元素進行對比看看是否相等，如果s串枚舉到的這個串和t串中的第j個相等。那么dp[j+1]+=dp[j]。你可能會問為啥是dp[j+1],因為第一個元素匹配到需要將數量+1，而這里為了避免這樣的判斷我們將dp[0]=1,這樣t串的每個元素都能正常的操作。

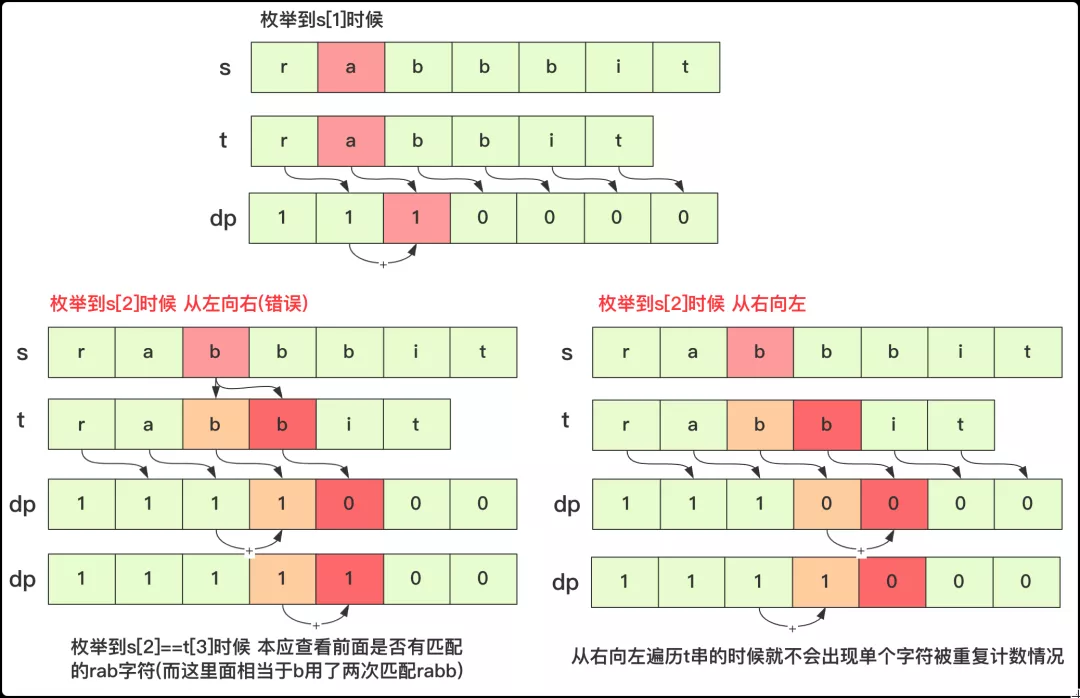
但是有一點需要注意的就是在遍歷s串中第i個字母的時候，遍歷t串比較不能從左向右而必須從右向左。因為在遍歷s串的第i個字符在枚舉dp數組時候要求此刻數據是相對靜止的疊加(即同一層次不能產生影響)，而從左往右進行遇到相同字符會對后面的值產生影響。區別的話可以參考下圖這個例子：

實現的代碼為：

class Solution { 
    public int numDistinct(String s, String t) { 
      char s1[]=s.toCharArray(); 
      char t1[]=t.toCharArray(); 
      int dp[]=new int[t1.length+1]; 
      dp[0]=1;//用來疊加 
 
      for(int i=0;i<s1.length;i++) 
      { 
        for(int j=t1.length-1;j>=0;j--) 
        { 
          if(t1[j]==s1[i]) 
          { 
            dp[j+1]+=dp[j]; 
          } 
        } 
      } 
      return dp[t1.length]; 
    } 
} 

結語

至此，簡單的動態規劃算是分享完了。

大部分簡單動態規劃還是有套路的，你看到一些數組問題、字符串問題很有可能就暗藏動態規劃。動態規劃的套路跟遞歸有點點相似，主要是找到狀態轉移方程，有時候考慮問題不能一步想的太多(想太多可能就把自己繞進去了)，而動態規劃就是要大家對數值上下轉換計算需要了解其中關系。

對于復雜dp問題或者很多套一層殼確實很難看出來，但是掌握上面的常見dp問題和背包問題，就可以解決大部分動態規劃問題啦(畢竟咱們不是搞競賽遇到的還是偏簡單或者中等難度的)。

本文轉載自微信公眾號「bigsai」