介紹

假設(shè)你是一所大學(xué)的老師。在對(duì)一周的作業(yè)進(jìn)行了檢查之后，你給所有的學(xué)生打了分?jǐn)?shù)。你把這些打了分?jǐn)?shù)的論文交給大學(xué)的數(shù)據(jù)錄入人員，并告訴他創(chuàng)建一個(gè)包含所有學(xué)生成績(jī)的電子表格。但這個(gè)人卻只存儲(chǔ)了成績(jī)，而沒(méi)有包含對(duì)應(yīng)的學(xué)生。

他又犯了另一個(gè)錯(cuò)誤，在匆忙中跳過(guò)了幾項(xiàng)，但我們卻不知道丟了誰(shuí)的成績(jī)。我們來(lái)看看如何來(lái)解決這個(gè)問(wèn)題吧。

一種方法是將成績(jī)可視化，看看是否可以在數(shù)據(jù)中找到某種趨勢(shì)。

 

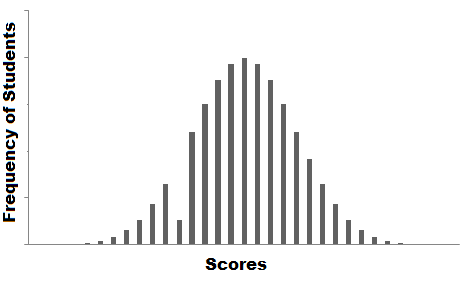
上面展示的圖形稱為數(shù)據(jù)的頻率分布。其中有一個(gè)平滑的曲線，但你注意到有一個(gè)異常情況了嗎?在某個(gè)特定的分?jǐn)?shù)范圍內(nèi)，數(shù)據(jù)的頻率異常低。所以，最準(zhǔn)確的猜測(cè)就是丟失值了，從而導(dǎo)致在分布中出現(xiàn)了凹陷。

這個(gè)過(guò)程展示了你該如何使用數(shù)據(jù)分析來(lái)嘗試解決現(xiàn)實(shí)生活中的問(wèn)題。對(duì)于任何一位數(shù)據(jù)科學(xué)家、學(xué)生或從業(yè)者來(lái)說(shuō)，分布是必須要知道的概念，它為分析和推理統(tǒng)計(jì)提供了基礎(chǔ)。

雖然概率為我們提供了數(shù)學(xué)上的計(jì)算，而分布卻可以幫助我們把內(nèi)部發(fā)生的事情可視化。

在本文中，我將介紹一些重要的概率分布，并會(huì)清晰全面地對(duì)它們進(jìn)行解釋。

注意：本文假設(shè)你已經(jīng)具有了概率方面的基本知識(shí)。如果沒(méi)有，可以參考這篇有關(guān)概率基礎(chǔ)的文章。

目錄

1、常見(jiàn)的數(shù)據(jù)類型

2、分布的類型

• 伯努利分布
• 均勻分布
• 二項(xiàng)分布
• 正態(tài)分布
• 泊松分布
• 指數(shù)分布

3、各個(gè)分布之間的關(guān)系

一、常見(jiàn)的數(shù)據(jù)類型

在開(kāi)始詳細(xì)講述分布之前，先來(lái)看看我們會(huì)遇到哪些種類的數(shù)據(jù)。數(shù)據(jù)可以分為離散的和連續(xù)的。

1. 離散數(shù)據(jù)：顧名思義，只包含指定的值。例如，當(dāng)你投骰子的時(shí)候，輸出結(jié)果只可能是1、2、3、4、5或6，而不可能出現(xiàn)1.5或2.45。
2. 連續(xù)數(shù)據(jù)：可以在給定的范圍內(nèi)取任何值。范圍可以是有限的，也可以是***的。例如，女孩的體重或身高、路程的長(zhǎng)度。女孩的體重可以是54千克、54.5千克，或54.5436千克。

現(xiàn)在我們開(kāi)始學(xué)習(xí)分布的類型。

2、分布的類型

2.1、伯努利分布

我們首先從最簡(jiǎn)單的分布伯努利分布開(kāi)始。

伯努利分布只有兩種可能的結(jié)果，1(成功)和0(失敗)。因此，具有伯努利分布的隨機(jī)變量X可以取值為1，也就是成功的概率，可以用p來(lái)表示，也可以取值為0，即失敗的概率，用q或1-p來(lái)表示。

概率質(zhì)量函數(shù)由下式給出：px(1-p)1-x， 其中x € (0, 1)。它也可以寫(xiě)成：

 

成功與失敗的概率不一定相等。這里，成功的概率(p)與失敗的概率不同。所以，下圖顯示了我們之間比賽結(jié)果的伯努利分布。

 

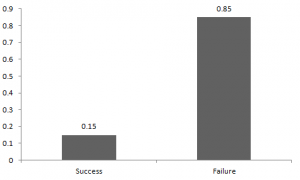
這里，成功的概率 = 0.15，失敗的概率 = 0.85 。如果我打了你，我可能會(huì)期待你向我打回來(lái)。任何分布的基本預(yù)期值是分布的平均值。來(lái)自伯努利分布的隨機(jī)變量X的期望值如為：

E(X) = 1p + 0(1-p) = p

隨機(jī)變量與二項(xiàng)分布的方差為：

V(X) = E(X²) – [E(X)]² = p – p² = p(1-p)

伯努利分布的例子有很多，比如說(shuō)明天是否要下雨，如果下雨則表示成功，如果不下雨，則表示失敗。

2.2、均勻分布

對(duì)于投骰子來(lái)說(shuō)，結(jié)果是1到6。得到任何一個(gè)結(jié)果的概率是相等的，這就是均勻分布的基礎(chǔ)。與伯努利分布不同，均勻分布的所有可能結(jié)果的n個(gè)數(shù)也是相等的。

如果變量X是均勻分布的，則密度函數(shù)可以表示為：

 

均勻分布的曲線是這樣的：

 

你可以看到，均勻分布曲線的形狀是一個(gè)矩形，這也是均勻分布又稱為矩形分布的原因。其中，a和b是參數(shù)。

花店每天銷售的花束數(shù)量是均勻分布的，最多為40，最少為10。我們來(lái)計(jì)算一下日銷售量在15到30之間的概率。

• 日銷售量在15到30之間的概率為(30-15)*(1/(40-10)) = 0.5
• 同樣地，日銷售量大于20的概率為 = 0.667

遵循均勻分布的X的平均值和方差為：

• 平均值 -> E(X) = (a+b)/2
• 方差 -> V(X) = (b-a)²/12

標(biāo)準(zhǔn)均勻密度的參數(shù) a = 0 和 b = 1，因此標(biāo)準(zhǔn)均勻密度由下式給出：

 

2.3、二項(xiàng)分布

讓我們來(lái)看看玩板球這個(gè)例子。假設(shè)你今天贏了一場(chǎng)比賽，這表示一個(gè)成功的事件。你再比了一場(chǎng)，但你輸了。如果你今天贏了一場(chǎng)比賽，但這并不表示你明天肯定會(huì)贏。我們來(lái)分配一個(gè)隨機(jī)變量X，用于表示贏得的次數(shù)。 X可能的值是多少呢?它可以是任意值，這取決于你擲硬幣的次數(shù)。

只有兩種可能的結(jié)果，成功和失敗。因此，成功的概率 = 0.5，失敗的概率可以很容易地計(jì)算得到：q = p – 1 = 0.5。

二項(xiàng)式分布就是只有兩個(gè)可能結(jié)果的分布，比如成功或失敗、得到或者丟失、贏或敗，每一次嘗試成功和失敗的概率相等。

結(jié)果有可能不一定相等。如果在實(shí)驗(yàn)中成功的概率為0.2，則失敗的概率可以很容易地計(jì)算得到 q = 1 - 0.2 = 0.8。

每一次嘗試都是獨(dú)立的，因?yàn)榍耙淮瓮稊S的結(jié)果不能決定或影響當(dāng)前投擲的結(jié)果。只有兩個(gè)可能的結(jié)果并且重復(fù)n次的實(shí)驗(yàn)叫做二項(xiàng)式。二項(xiàng)分布的參數(shù)是n和p，其中n是試驗(yàn)的總數(shù)，p是每次試驗(yàn)成功的概率。

在上述說(shuō)明的基礎(chǔ)上，二項(xiàng)式分布的屬性包括：

• 每個(gè)試驗(yàn)都是獨(dú)立的。
• 在試驗(yàn)中只有兩個(gè)可能的結(jié)果：成功或失敗。
• 總共進(jìn)行了n次相同的試驗(yàn)。
• 所有試驗(yàn)成功和失敗的概率是相同的。 (試驗(yàn)是一樣的)

二項(xiàng)分布的數(shù)學(xué)表示由下式給出：

 

成功概率不等于失敗概率的二項(xiàng)分布圖：

 

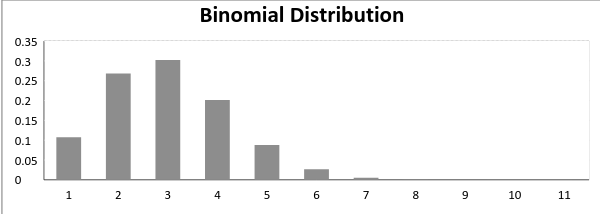
現(xiàn)在，當(dāng)成功的概率 = 失敗的概率時(shí)，二項(xiàng)分布圖如下

 

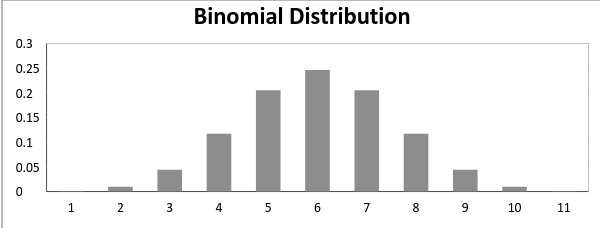
二項(xiàng)分布的均值和方差由下式給出：

• 平均值 -> µ = n*p
• 方差 -> Var(X) = npq

2.4、正態(tài)分布

正態(tài)分布代表了宇宙中大多數(shù)情況的運(yùn)轉(zhuǎn)狀態(tài)。大量的隨機(jī)變量被證明是正態(tài)分布的。任何一個(gè)分布只要具有以下特征，則可以稱為正態(tài)分布：

• 分布的平均值、中位數(shù)和模式一致。
• 分布曲線是鐘形的，關(guān)于線 x = μ 對(duì)稱。
• 曲線下的總面積為1。
• 有一半的值在中心的左邊，另一半在右邊。
• 正態(tài)分布與二項(xiàng)分布有著很大的不同。然而，如果試驗(yàn)次數(shù)接近于無(wú)窮大，則它們的形狀會(huì)變得十分相似。

遵循正態(tài)分布的隨機(jī)變量X的值由下式給出：

 

正態(tài)分布的隨機(jī)變量X的均值和方差由下式給出：

• 均值 -> E(X) = µ
• 方差 -> Var(X) = σ^2

其中，μ(平均)和σ(標(biāo)準(zhǔn)偏差)是參數(shù)。

隨機(jī)變量X〜N(μ，σ)的圖如下所示。

 

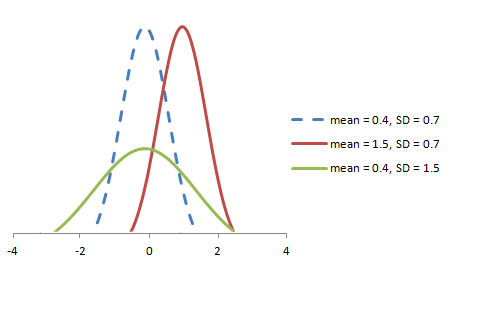
標(biāo)準(zhǔn)正態(tài)分布定義為平均值等于0，標(biāo)準(zhǔn)偏差等于1的分布：

 

 

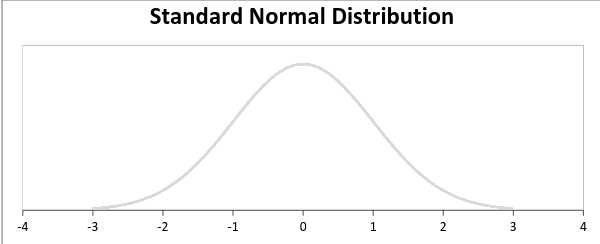
2.5、泊松分布

假設(shè)你在一個(gè)呼叫中心工作，一天里你大概會(huì)接到多少個(gè)電話?它可以是任何一個(gè)數(shù)字。現(xiàn)在，呼叫中心一天的呼叫總數(shù)可以用泊松分布來(lái)建模。這里有一些例子：

• 醫(yī)院在一天內(nèi)錄制的緊急電話的數(shù)量。
• 某個(gè)地區(qū)在一天內(nèi)報(bào)告的失竊的數(shù)量。
• 在一小時(shí)內(nèi)抵達(dá)沙龍的客戶人數(shù)。
• 在特定城市上報(bào)的自殺人數(shù)。
• 書(shū)中每一頁(yè)打印錯(cuò)誤的數(shù)量。
• 泊松分布適用于在隨機(jī)時(shí)間和空間上發(fā)生事件的情況，其中，我們只關(guān)注事件發(fā)生的次數(shù)。

當(dāng)以下假設(shè)有效時(shí)，則稱為泊松分布：

• 任何一個(gè)成功的事件都不應(yīng)該影響另一個(gè)成功的事件。
• 在短時(shí)間內(nèi)成功的概率必須等于在更長(zhǎng)的間內(nèi)成功的概率。
• 時(shí)間間隔變小時(shí)，在給間隔時(shí)間內(nèi)成功的概率趨向于零。

泊松分布中使用了這些符號(hào)：

• λ是事件發(fā)生的速率
• t是時(shí)間間隔的長(zhǎng)
• X是該時(shí)間間隔內(nèi)的事件數(shù)。
• 其中，X稱為泊松隨機(jī)變量，X的概率分布稱為泊松分布。
• 令μ表示長(zhǎng)度為t的間隔中的平均事件數(shù)。那么，µ = λ*t。

泊松分布的X由下式給出：

 

平均值μ是該分布的參數(shù)。 μ也定義為該間隔的λ倍長(zhǎng)度。泊松分布圖如下所示：

 

下圖顯示了隨著平均值的增加曲線的偏移情況：

 

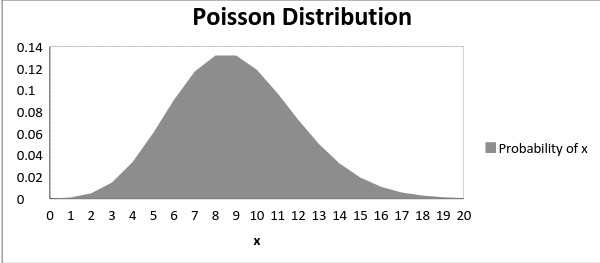
可以看出，隨著平均值的增加，曲線向右移動(dòng)。

泊松分布中X的均值和方差：

• 均值 -> E(X) = µ
• 方差 -> Var(X) = µ

2.6、指數(shù)分布

讓我們?cè)僖淮慰纯春艚兄行牡哪莻€(gè)例子。不同呼叫之間的時(shí)間間隔是多少呢?在這里，指數(shù)分布模擬了呼叫之間的時(shí)間間隔。

其他類似的例子有：

• 地鐵到達(dá)時(shí)間間隔
• 到達(dá)加油站的時(shí)間
• 空調(diào)的壽命

指數(shù)分布廣泛用于生存分析。從機(jī)器的預(yù)期壽命到人類的預(yù)期壽命，指數(shù)分布都能成功地提供結(jié)果。

具有的指數(shù)分布的隨機(jī)變量X：

• f(x) = { λe-λx, x ≥ 0
• 參數(shù) λ>0 也稱為速率。

對(duì)于生存分析，λ被稱為任何時(shí)刻t的設(shè)備的故障率，假定它已經(jīng)存活到t時(shí)刻。

遵循指數(shù)分布的隨機(jī)變量X的均值和方差為：

• 平均值 -> E(X) = 1/λ
• 方差 -> Var(X) = (1/λ)²

此外，速率越大，曲線下降越快，速率越慢，曲線越平坦。下面的圖很好地解釋了這一點(diǎn)。

 

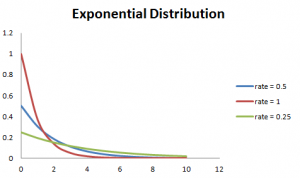
為了簡(jiǎn)化計(jì)算，下面給出一些公式。

• P{X≤x} = 1 – e-λx 對(duì)應(yīng)于x左側(cè)曲線下的面積。
• PP{X>x} = e-λx 對(duì)應(yīng)于x右側(cè)曲線下的面積。
• P{x1-λx1 – e-λx2, corresponds to the area under the density curve between x1 and x2.
• P{x1-λx1 – e-λx2 對(duì)應(yīng)于x1和x2之間地曲線下的面積。

3、各種分布之間的關(guān)系

伯努利與二項(xiàng)分布之間的關(guān)系

• 伯努利分布是具有單項(xiàng)試驗(yàn)的二項(xiàng)式分布的特殊情況。
• 伯努利分布和二項(xiàng)式分布只有兩種可能的結(jié)果，即成功與失敗。
• 伯努利分布和二項(xiàng)式分布都具有獨(dú)立的軌跡。

泊松與二項(xiàng)式分布之間的關(guān)系

泊松分布在滿足以下條件的情況下是二項(xiàng)式分布的極限情況：

• 試驗(yàn)次數(shù)***大或n → ∞。
• 每個(gè)試驗(yàn)成功的概率是相同的，***小的，或p → 0。
• np = λ，是有限的。

正態(tài)分布與二項(xiàng)式分布之間的關(guān)系，以及正態(tài)分布與泊松分布之間的關(guān)系

正態(tài)分布是在滿足以下條件的情況下二項(xiàng)分布的另一種限制形式：

• 試驗(yàn)次數(shù)***大，n → ∞。
• p和q都不是***小。

正態(tài)分布也是參數(shù)λ → ∞的泊松分布的極限情況。

指數(shù)和泊松分布之間的關(guān)系

如果隨機(jī)事件之間的時(shí)間遵循速率為λ的指數(shù)分布，則時(shí)間長(zhǎng)度t內(nèi)的事件總數(shù)遵循具有參數(shù)λt的泊松分布。

結(jié)束語(yǔ)

概率分布在許多領(lǐng)域都很常見(jiàn)，包括保險(xiǎn)、物理、工程、計(jì)算機(jī)科學(xué)甚至社會(huì)科學(xué)，如心理學(xué)和醫(yī)學(xué)。它易于應(yīng)用，并應(yīng)用很廣泛。本文重點(diǎn)介紹了日常生活中經(jīng)常能遇到的六個(gè)重要分布，并解釋了它們的應(yīng)用。現(xiàn)在，你已經(jīng)能夠識(shí)別、關(guān)聯(lián)和區(qū)分這些分布了。