從重采樣到數(shù)據(jù)合成：如何處理機(jī)器學(xué)習(xí)中的不平衡分類問題？

作者：機(jī)器之心編譯 2017-03-20 09:25:10

這篇文章描述了使用多種采樣技術(shù)來解決這種類別不平衡問題的各種方法。本文還比較了每種技術(shù)的優(yōu)缺點(diǎn)。

如果你研究過一點(diǎn)機(jī)器學(xué)習(xí)和數(shù)據(jù)科學(xué)，你肯定遇到過不平衡的類分布(imbalanced class distribution)。這種情況是指：屬于某一類別的觀測樣本的數(shù)量顯著少于其它類別。

這個問題在異常檢測是至關(guān)重要的的場景中很明顯，例如電力盜竊、銀行的欺詐交易、罕見疾病識別等。在這種情況下，利用傳統(tǒng)機(jī)器學(xué)習(xí)算法開發(fā)出的預(yù)測模型可能會存在偏差和不準(zhǔn)確。

發(fā)生這種情況的原因是機(jī)器學(xué)習(xí)算法通常被設(shè)計成通過減少誤差來提高準(zhǔn)確率。所以它們并沒有考慮類別的分布/比例或者是類別的平衡。

[[185791]]

這篇指南描述了使用多種采樣技術(shù)來解決這種類別不平衡問題的各種方法。本文還比較了每種技術(shù)的優(yōu)缺點(diǎn)。最后，本文作者還向我們展示了一種讓你可以創(chuàng)建一個平衡的類分布的方法，讓你可以應(yīng)用專門為此設(shè)計的集成學(xué)習(xí)技術(shù)(ensemble learning technique)。

1. 不平衡數(shù)據(jù)集面臨的挑戰(zhàn)

2. 處理不平衡數(shù)據(jù)集的方法

3. 例證

4. 結(jié)論

一、不平衡數(shù)據(jù)集面臨的挑戰(zhàn)

當(dāng)今公用事業(yè)行業(yè)面臨的主要挑戰(zhàn)之一就是電力盜竊。電力盜竊是全球第三大盜竊形式。越來越多的公用事業(yè)公司傾向于使用高級的數(shù)據(jù)分析技術(shù)和機(jī)器學(xué)習(xí)算法來識別代表盜竊的消耗模式。

然而，最大的障礙之一就是海量的數(shù)據(jù)及其分布。欺詐性交易的數(shù)量要遠(yuǎn)低于正常和健康的交易，也就是說，它只占到了總觀測量的大約 1-2%。這里的問題是提高識別罕見的少數(shù)類別的準(zhǔn)確率，而不是實(shí)現(xiàn)更高的總體準(zhǔn)確率。

當(dāng)面臨不平衡的數(shù)據(jù)集的時候，機(jī)器學(xué)習(xí)算法傾向于產(chǎn)生不太令人滿意的分類器。對于任何一個不平衡的數(shù)據(jù)集，如果要預(yù)測的事件屬于少數(shù)類別，并且事件比例小于 5%，那就通常將其稱為罕見事件(rare event)。

1. 不平衡類別的實(shí)例

讓我們借助一個實(shí)例來理解不平衡類別。

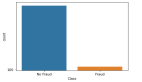
例子：在一個公用事業(yè)欺詐檢測數(shù)據(jù)集中，你有以下數(shù)據(jù)：

總觀測 = 1000
欺詐觀測 = 20
非欺詐觀測 = 980
罕見事件比例 = 2%

這個案例的數(shù)據(jù)分析中面臨的主要問題是：對于這些先天就是小概率的異常事件，如何通過獲取合適數(shù)量的樣本來得到一個平衡的數(shù)據(jù)集?

2. 使用標(biāo)準(zhǔn)機(jī)器學(xué)習(xí)技術(shù)時面臨的挑戰(zhàn)

面臨不平衡數(shù)據(jù)集的時候，傳統(tǒng)的機(jī)器學(xué)習(xí)模型的評價方法不能精確地衡量模型的性能。

諸如決策樹和 Logistic 回歸這些標(biāo)準(zhǔn)的分類算法會偏向于數(shù)量多的類別。它們往往會僅預(yù)測占數(shù)據(jù)大多數(shù)的類別。在總量中占少數(shù)的類別的特征就會被視為噪聲，并且通常會被忽略。因此，與多數(shù)類別相比，少數(shù)類別存在比較高的誤判率。

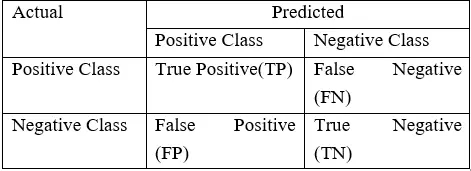
對分類算法的表現(xiàn)的評估是用一個包含關(guān)于實(shí)際類別和預(yù)測類別信息的混淆矩陣(Confusion Matrix)來衡量的。

如上表所示，模型的準(zhǔn)確率 = (TP+TN) / (TP+FN+FP+TP)

然而，在不平衡領(lǐng)域時，準(zhǔn)確率并不是一個用來衡量模型性能的合適指標(biāo)。例如：一個分類器，在包含 2% 的罕見事件時，如果它將所有屬于大部分類別的實(shí)例都正確分類，實(shí)現(xiàn)了 98% 的準(zhǔn)確率;而把占 2% 的少數(shù)觀測數(shù)據(jù)視為噪聲并消除了。

3. 不平衡類別的實(shí)例

因此，總結(jié)一下，在嘗試?yán)貌黄胶鈹?shù)據(jù)集解決特定業(yè)務(wù)的挑戰(zhàn)時，由標(biāo)準(zhǔn)機(jī)器學(xué)習(xí)算法生成的分類器可能無法給出準(zhǔn)確的結(jié)果。除了欺詐性交易，存在不平衡數(shù)據(jù)集問題的常見業(yè)務(wù)問題還有：

識別客戶流失率的數(shù)據(jù)集，其中絕大多數(shù)顧客都會繼續(xù)使用該項服務(wù)。具體來說，電信公司中，客戶流失率低于 2%。
醫(yī)療診斷中識別罕見疾病的數(shù)據(jù)集
自然災(zāi)害，例如地震

4. 使用的數(shù)據(jù)集

這篇文章中，我們會展示多種在高度不平衡數(shù)據(jù)集上訓(xùn)練一個性能良好的模型的技術(shù)。并且用下面的欺詐檢測數(shù)據(jù)集來精確地預(yù)測罕見事件：

總觀測 = 1000
欺詐觀測 = 20
非欺詐性觀測 = 980
事件比例 = 2%
欺詐類別標(biāo)志 = 0(非欺詐實(shí)例)
欺詐類別標(biāo)志 = 1(欺詐實(shí)例)

二、處理不平衡數(shù)據(jù)集的方法

1. 數(shù)據(jù)層面的方法：重采樣技術(shù)

處理不平衡數(shù)據(jù)集需要在往機(jī)器學(xué)習(xí)算法輸入數(shù)據(jù)之前，制定諸如提升分類算法或平衡訓(xùn)練數(shù)據(jù)的類(數(shù)據(jù)預(yù)處理)的策略。后者因為應(yīng)用范圍廣泛而更常使用。

平衡分類的主要目標(biāo)不是增加少數(shù)類的的頻率就是降低多數(shù)類的頻率。這樣做是為了獲得大概相同數(shù)量的兩個類的實(shí)例。讓我們一起看看幾個重采樣(resampling)技術(shù)：

（1）隨機(jī)欠采樣(Random Under-Sampling)

隨機(jī)欠采樣的目標(biāo)是通過隨機(jī)地消除占多數(shù)的類的樣本來平衡類分布;直到多數(shù)類和少數(shù)類的實(shí)例實(shí)現(xiàn)平衡，目標(biāo)才算達(dá)成。

總觀測 = 1000
欺詐性觀察 = 20
非欺詐性觀察 = 980
事件發(fā)生率 = 2%

這種情況下我們不重復(fù)地從非欺詐實(shí)例中取 10% 的樣本，并將其與欺詐性實(shí)例相結(jié)合。

隨機(jī)欠采樣之后的非欺詐性觀察 = 980 x 10% = 98

結(jié)合欺詐性與非欺詐性觀察之后的全體觀察 = 20+98 = 118

欠采樣之后新數(shù)據(jù)集的事件發(fā)生率 = 20/118 = 17%

優(yōu)點(diǎn)

它可以提升運(yùn)行時間;并且當(dāng)訓(xùn)練數(shù)據(jù)集很大時，可以通過減少樣本數(shù)量來解決存儲問題。

缺點(diǎn)

它會丟棄對構(gòu)建規(guī)則分類器很重要的有價值的潛在信息。
被隨機(jī)欠采樣選取的樣本可能具有偏差。它不能準(zhǔn)確代表大多數(shù)。從而在實(shí)際的測試數(shù)據(jù)集上得到不精確的結(jié)果。

（2）隨機(jī)過采樣(Random Over-Sampling)

過采樣(Over-Sampling)通過隨機(jī)復(fù)制少數(shù)類來增加其中的實(shí)例數(shù)量，從而可增加樣本中少數(shù)類的代表性。

總觀測 = 1000
欺詐性觀察 = 20
非欺詐性觀察 = 980
事件發(fā)生率 = 2%

這種情況下我們復(fù)制 20 個欺詐性觀察 20 次。

非欺詐性觀察 = 980
復(fù)制少數(shù)類觀察之后的欺詐性觀察 = 400
過采樣之后新數(shù)據(jù)集中的總體觀察 = 1380
欠采樣之后新數(shù)據(jù)集的事件發(fā)生率 = 400/1380 = 29%

優(yōu)點(diǎn)

與欠采樣不同，這種方法不會帶來信息損失。
表現(xiàn)優(yōu)于欠采樣。

缺點(diǎn)

由于復(fù)制少數(shù)類事件，它加大了過擬合的可能性。

（3）基于聚類的過采樣(Cluster-Based Over Sampling)

在這種情況下，K-均值聚類算法獨(dú)立地被用于少數(shù)和多數(shù)類實(shí)例。這是為了識別數(shù)據(jù)集中的聚類。隨后，每一個聚類都被過采樣以至于相同類的所有聚類有著同樣的實(shí)例數(shù)量，且所有的類有著相同的大小。

總觀測 = 1000
欺詐性觀察 = 20
非欺詐性觀察 = 980
事件發(fā)生率 = 2%

多數(shù)類聚類

1. 聚類 1：150 個觀察
2. 聚類 2：120 個觀察
3. 聚類 3：230 個觀察
4. 聚類 4：200 個觀察
5. 聚類 5：150 個觀察
6. 聚類 6：130 個觀察

少數(shù)類聚類

1. 聚類 1：8 個觀察
2. 聚類 2：12 個觀察

每個聚類過采樣之后，相同類的所有聚類包含相同數(shù)量的觀察。

多數(shù)類聚類

1. 聚類 1：170 個觀察
2. 聚類 2：170 個觀察
3. 聚類 3：170 個觀察
4. 聚類 4：170 個觀察
5. 聚類 5：170 個觀察
6. 聚類 6：170 個觀察

少數(shù)類聚類

1. 聚類 1：250 個觀察
2. 聚類 2：250 個觀察

基于聚類的過采樣之后的事件率 = 500/ (1020+500) = 33 %

優(yōu)點(diǎn)

這種聚類技術(shù)有助于克服類之間不平衡的挑戰(zhàn)。表示正例的樣本數(shù)量不同于表示反例的樣本數(shù)量。
有助于克服由不同子聚類組成的類之間的不平衡的挑戰(zhàn)。每一個子聚類不包含相同數(shù)量的實(shí)例。

缺點(diǎn)

正如大多數(shù)過采樣技術(shù)，這一算法的主要缺點(diǎn)是有可能過擬合訓(xùn)練集。

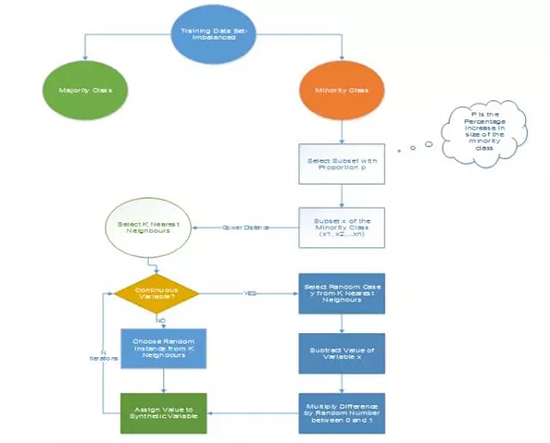
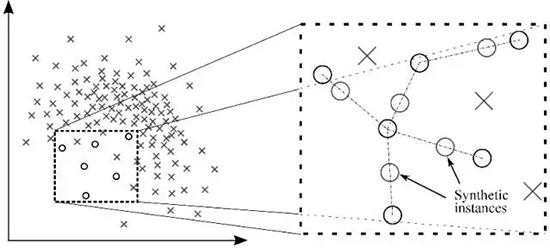
（4）信息性過采樣：合成少數(shù)類過采樣技術(shù)(SMOTE)

這一技術(shù)可用來避免過擬合——當(dāng)直接復(fù)制少數(shù)類實(shí)例并將其添加到主數(shù)據(jù)集時。從少數(shù)類中把一個數(shù)據(jù)子集作為一個實(shí)例取走，接著創(chuàng)建相似的新合成的實(shí)例。這些合成的實(shí)例接著被添加進(jìn)原來的數(shù)據(jù)集。新數(shù)據(jù)集被用作樣本以訓(xùn)練分類模型。

總觀測 = 1000
欺詐性觀察 = 20
非欺詐性觀察 = 980
事件發(fā)生率 = 2%

從少數(shù)類中取走一個包含 15 個實(shí)例的樣本，并生成相似的合成實(shí)例 20 次。

生成合成性實(shí)例之后，創(chuàng)建下面的數(shù)據(jù)集

少數(shù)類(欺詐性觀察)= 300
多數(shù)類(非欺詐性觀察)= 980
事件發(fā)生率 = 300/1280 = 23.4 %

優(yōu)點(diǎn)

通過隨機(jī)采樣生成的合成樣本而非實(shí)例的副本，可以緩解過擬合的問題。
不會損失有價值信息。

缺點(diǎn)

當(dāng)生成合成性實(shí)例時，SMOTE 并不會把來自其他類的相鄰實(shí)例考慮進(jìn)來。這導(dǎo)致了類重疊的增加，并會引入額外的噪音。
SMOTE 對高維數(shù)據(jù)不是很有效。

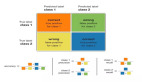
圖 1：合成少數(shù)類過采樣算法，其中 N 是屬性的數(shù)量

圖 2：借助 SMOTE 的合成實(shí)例生成

（5）改進(jìn)的合成少數(shù)類過采樣技術(shù)(MSMOTE)

這是 SMOTE 的改進(jìn)版本，SMOTE 沒有考慮數(shù)據(jù)集中少數(shù)類和潛在噪聲的基本分布。所以為了提高 SMOTE 的效果，MSMOTE 應(yīng)運(yùn)而生。

該算法將少數(shù)類別的樣本分為 3 個不同的組：安全樣本、邊界樣本和潛在噪聲樣本。分類通過計算少數(shù)類的樣本和訓(xùn)練數(shù)據(jù)的樣本之間的距離來完成。安全樣本是可以提高分類器性能的那些數(shù)據(jù)點(diǎn)。而另一方面，噪聲是可以降低分類器的性能的數(shù)據(jù)點(diǎn)。兩者之間的那些數(shù)據(jù)點(diǎn)被分類為邊界樣本。

雖然 MSOMTE 的基本流程與 SMOTE 的基本流程相同，在 MSMOTE 中，選擇近鄰的策略不同于 SMOTE。該算法是從安全樣本出發(fā)隨機(jī)選擇 k-最近鄰的數(shù)據(jù)點(diǎn)，并從邊界樣本出發(fā)選擇最近鄰，并且不對潛在噪聲樣本進(jìn)行任何操作。

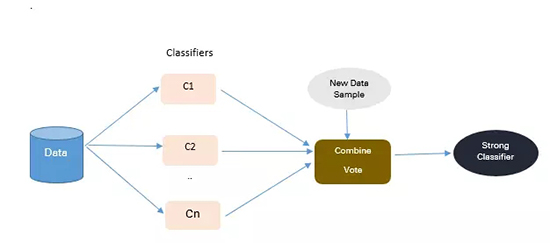
2. 算法集成技術(shù)(Algorithmic Ensemble Techniques)

上述部分涉及通過重采樣原始數(shù)據(jù)提供平衡類來處理不平衡數(shù)據(jù)，在本節(jié)中，我們將研究一種替代方法：修改現(xiàn)有的分類算法，使其適用于不平衡數(shù)據(jù)集。

集成方法的主要目的是提高單個分類器的性能。該方法從原始數(shù)據(jù)中構(gòu)建幾個兩級分類器，然后整合它們的預(yù)測。

圖 3：基于集成的方法

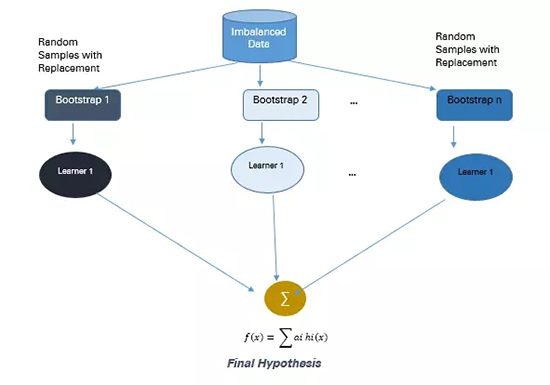
（1）基于 Bagging 的方法

Bagging 是 Bootstrap Aggregating 的縮寫。傳統(tǒng)的 Bagging 算法包括生成「n」個不同替換的引導(dǎo)訓(xùn)練樣本，并分別訓(xùn)練每個自舉算法上的算法，然后再聚合預(yù)測。

Bagging 常被用于減少過擬合，以提高學(xué)習(xí)效果生成準(zhǔn)確預(yù)測。與 boosting 不同，bagging 方法允許在自舉樣本中進(jìn)行替換。

圖 4：Bagging 方法

總觀測= 1000
欺詐觀察= 20
非欺詐觀察= 980
事件率= 2%

從具有替換的群體中選擇 10 個自舉樣品。每個樣本包含 200 個觀察值。每個樣本都不同于原始數(shù)據(jù)集，但類似于分布和變化上與該數(shù)據(jù)集類似。機(jī)器學(xué)習(xí)算法(如 logistic 回歸、神經(jīng)網(wǎng)絡(luò)與決策樹)擬合包含 200 個觀察的自舉樣本，且分類器 c1，c2 ... c10 被聚合以產(chǎn)生復(fù)合分類器。這種集成方法能產(chǎn)生更強(qiáng)的復(fù)合分類器，因為它組合了各個分類器的結(jié)果。

優(yōu)點(diǎn)

提高了機(jī)器學(xué)習(xí)算法的穩(wěn)定性與準(zhǔn)確性
減少方差
減少了 bagged 分類器的錯誤分類
在嘈雜的數(shù)據(jù)環(huán)境中，bagging 的性能優(yōu)于 boosting

缺點(diǎn)

bagging 只會在基本分類器效果很好時才有效。錯誤的分類可能會進(jìn)一步降低表現(xiàn)。

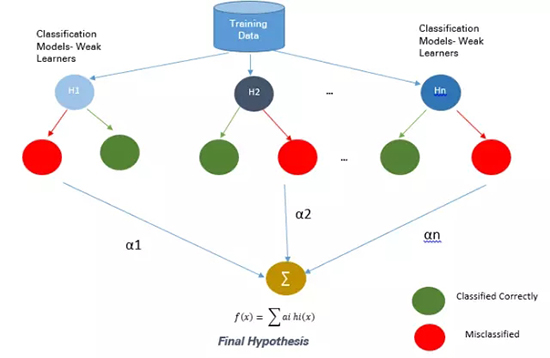
（2）基于 Boosting 的方法

Boosting 是一種集成技術(shù)，它可以將弱學(xué)習(xí)器結(jié)合起來創(chuàng)造出一個能夠進(jìn)行準(zhǔn)確預(yù)測的強(qiáng)大學(xué)習(xí)器。Boosting 開始于在訓(xùn)練數(shù)據(jù)上準(zhǔn)備的基本分類器/弱分類器。

基本學(xué)習(xí)器/分類器是弱學(xué)習(xí)器，即預(yù)測準(zhǔn)確度僅略好于平均水平。弱是指當(dāng)數(shù)據(jù)的存在小變化時，會引起分類模型出現(xiàn)大的變化。

在下一次迭代中，新分類器將重點(diǎn)放在那些在上一輪中被錯誤分類的案例上。

圖 5：Boosting 方法

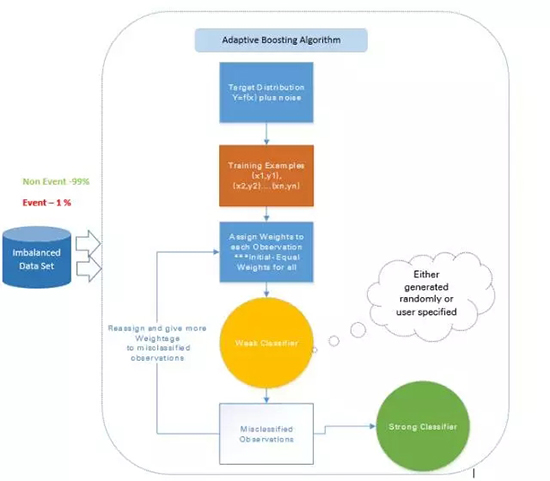
a. 自適應(yīng) boosting——Ada Boost

Ada Boost 是最早的 boosting 技術(shù)，其能通過許多弱的和不準(zhǔn)確的規(guī)則的結(jié)合來創(chuàng)造高準(zhǔn)確度的預(yù)測。其中每個訓(xùn)練器都是被串行地訓(xùn)練的，其目標(biāo)在每一輪正確分類上一輪沒能正確分類的實(shí)例。

對于一個學(xué)習(xí)過的分類器，如果要做出強(qiáng)大的預(yù)測，其應(yīng)該具備以下三個條件：

規(guī)則簡單
分類器在足夠數(shù)量的訓(xùn)練實(shí)例上進(jìn)行了訓(xùn)練
分類器在訓(xùn)練實(shí)例上的訓(xùn)練誤差足夠低

每一個弱假設(shè)都有略優(yōu)于隨機(jī)猜測的準(zhǔn)確度，即誤差項 € (t) 應(yīng)該略大約 ½-β，其中 β>0。這是這種 boosting 算法的基礎(chǔ)假設(shè)，其可以產(chǎn)生一個僅有一個很小的誤差的最終假設(shè)。

在每一輪之后，它會更加關(guān)注那些更難被分類的實(shí)例。這種關(guān)注的程度可以通過一個權(quán)重值(weight)來測量。起初，所有實(shí)例的權(quán)重都是相等的，經(jīng)過每一次迭代之后，被錯誤分類的實(shí)例的權(quán)重會增大，而被正確分類的實(shí)例的權(quán)重則會減小。

圖 6：自適應(yīng) boosting 的方法

比如如果有一個包含了 1000 次觀察的數(shù)據(jù)集，其中有 20 次被標(biāo)記為了欺詐。剛開始，所有的觀察都被分配了相同的權(quán)重 W1，基礎(chǔ)分類器準(zhǔn)確分類了其中 400 次觀察。

然后，那 600 次被錯誤分類的觀察的權(quán)重增大為 W2，而這 400 次被正確分類的實(shí)例的權(quán)重減小為 W3。

在每一次迭代中，這些更新過的加權(quán)觀察都會被送入弱的分類器以提升其表現(xiàn)。這個過程會一直持續(xù)，直到錯誤分類率顯著降低，從而得到一個強(qiáng)大的分類器。

優(yōu)點(diǎn)

非常簡單就能實(shí)現(xiàn)

可以很好地泛化——適合任何類型的分類問題且不易過擬合

缺點(diǎn)

對噪聲數(shù)據(jù)和異常值敏感

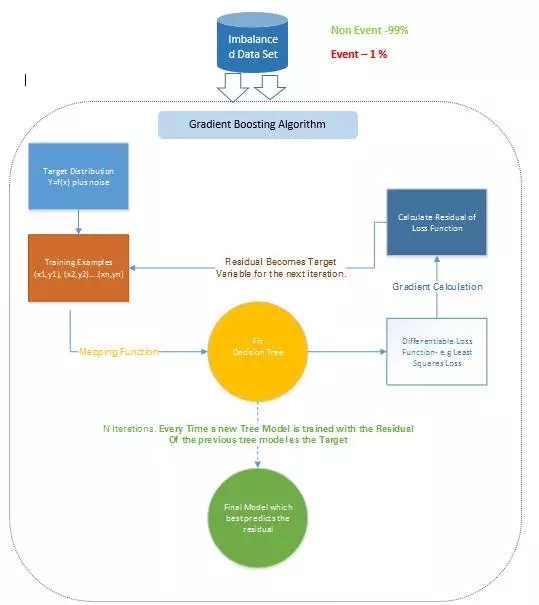
b. 梯度樹 boosting

在梯度 Boosting(Gradient Boosting)中，許多模型都是按順序訓(xùn)練的。其是一種數(shù)值優(yōu)化算法，其中每個模型都使用梯度下降(Gradient Descent)方法來最小化損失函數(shù) y = ax+b+e。

在梯度 Boosting 中，決策樹(Decision Tree)被用作弱學(xué)習(xí)器。

盡管 Ada Boost 和梯度 Boosting 都是基于弱學(xué)習(xí)器/分類器工作的，而且都是在努力使它們變成強(qiáng)大的學(xué)習(xí)器，但這兩種方法之間存在一些顯著的差異。Ada Boost 需要在實(shí)際的訓(xùn)練過程之前由用戶指定一組弱學(xué)習(xí)器或隨機(jī)生成弱學(xué)習(xí)器。其中每個學(xué)習(xí)器的權(quán)重根據(jù)其每步是否正確執(zhí)行了分類而進(jìn)行調(diào)整。而梯度 Boosting 則是在訓(xùn)練數(shù)據(jù)集上構(gòu)建第一個用來預(yù)測樣本的學(xué)習(xí)器，然后計算損失(即真實(shí)值和第一個學(xué)習(xí)器的輸出之間的差)，然后再使用這個損失在第二個階段構(gòu)建改進(jìn)了的學(xué)習(xí)器。

在每一個步驟，該損失函數(shù)的殘差(residual)都是用梯度下降法計算出來的，而新的殘差會在后續(xù)的迭代中變成目標(biāo)變量。

梯度 Boosting 可以通過 R 語言使用 SAS Miner 和 GBM 軟件包中的 Gradient Boosting Node 實(shí)現(xiàn)。

圖 7：梯度 Boosting 方法

比如，如果有一個包含了 1000 次觀察的訓(xùn)練數(shù)據(jù)集，其中有 20 次被標(biāo)記為了欺詐，并且還有一個初始的基礎(chǔ)分類器。目標(biāo)變量為 Fraud，當(dāng)交易是欺詐時，F(xiàn)raud=1;當(dāng)交易不是欺詐時，F(xiàn)raud=0.

比如說，決策樹擬合的是準(zhǔn)確分類僅 5 次觀察為欺詐觀察的情況。然后基于該步驟的實(shí)際輸出和預(yù)測輸出之間的差，計算出一個可微的損失函數(shù)。該損失函數(shù)的這個殘差是下一次迭代的目標(biāo)變量 F1。

類似地，該算法內(nèi)部計算該損失函數(shù)，并在每個階段更新該目標(biāo)，然后在初始分類器的基礎(chǔ)上提出一個改進(jìn)過的分類器。

缺點(diǎn)

梯度增強(qiáng)過的樹比隨機(jī)森林更難擬合
梯度 Boosting 算法通常有 3 個可以微調(diào)的參數(shù)：收縮(shrinkage)參數(shù)、樹的深度和樹的數(shù)量。要很好擬合，每個參數(shù)都需要合適的訓(xùn)練。如果這些參數(shù)沒有得到很好的調(diào)節(jié)，那么就可能會導(dǎo)致過擬合。

c. XGBoost

XGBoost(Extreme Gradient Boosting/極限梯度提升)是 Gradient Boosting 算法的一種更先進(jìn)和更有效的實(shí)現(xiàn)。

相對于其它 Boosting 技術(shù)的優(yōu)點(diǎn)：

速度比普通的 Gradient Boosting 快 10 倍，因為其可以實(shí)現(xiàn)并行處理。它是高度靈活的，因為用戶可以自定義優(yōu)化目標(biāo)和評估標(biāo)準(zhǔn)，其具有內(nèi)置的處理缺失值的機(jī)制。
和遇到了負(fù)損失就會停止分裂節(jié)點(diǎn)的 Gradient Boosting 不同，XGBoost 會分裂到指定的最大深度，然后會對其樹進(jìn)行反向的剪枝(prune)，移除僅有一個負(fù)損失的分裂。

XGBoost 可以使用 R 和 Python 中的 XGBoost 包實(shí)現(xiàn)。

三、實(shí)際案例

1. 數(shù)據(jù)描述

這個例子使用了電信公司的包含了 47241 條顧客記錄的數(shù)據(jù)集，每條記錄包含的信息有 27 個關(guān)鍵預(yù)測變量

罕見事件數(shù)據(jù)集的數(shù)據(jù)結(jié)構(gòu)如下，缺失值刪除、異常值處理以及降維

從這里下載數(shù)據(jù)集：

https://static.analyticsvidhya.com/wp-content/uploads/2017/03/17063705/SampleData_IMC.csv

2. 方法描述

使用合成少數(shù)類過采樣技術(shù)(SMOTE)來平衡不平衡數(shù)據(jù)集——該技術(shù)是試圖通過創(chuàng)建合成實(shí)例來平衡數(shù)據(jù)集。下面以 R 代碼為例，示范使用 Gradient Boosting 算法來訓(xùn)練平衡數(shù)據(jù)集。

R 代碼 
# 加載數(shù)據(jù) 
rareevent_boost <- read.table("D:/Upasana/RareEvent/churn.txt",sep="|", header=TRUE) 
dmy<-dummyVars("~.",data=rareevent_boost) 
rareeventTrsf<-data.frame(predict(dmy,newdata= rareevent_boost)) 
set.seed(10) 
sub <- sample(nrow(rareeventTrsf), floor(nrow(rareeventTrsf) * 0.9)) 
sub1 <- sample(nrow(rareeventTrsf), floor(nrow(rareeventTrsf) * 0.1)) 
training <- rareeventTrsf [sub, ] 
testing <- rareeventTrsf [-sub, ] 
training_sub<- rareeventTrsf [sub1, ] 
tables(training_sub) 
head(training_sub) 
# 對于不平衡的數(shù)據(jù)集 # 
install.packages("unbalanced") 
library(unbalanced) 
data(ubIonosphere) 
n<-ncol(rareevent_boost) 
output<- rareevent_boost $CHURN_FLAG 
output<-as.factor(output) 
input<- rareevent_boost [ ,-n] 
View(input) 
# 使用 ubSMOTE 來平衡數(shù)據(jù)集 # 
data<-ubBalance(X= input, Y=output, type="ubSMOTE", percOver=300, percUnder=150, verbose=TRUE 
View(data) 
# 平衡的數(shù)據(jù)集 # 
balancedData<-cbind(data$X,data$Y) 
View(balancedData) 
table(balancedData$CHURN_FLAG) 
# 寫入平衡的數(shù)據(jù)集來訓(xùn)練模型 # 
write.table(balancedData,"D:/ Upasana/RareEvent /balancedData.txt", sep="\t", row.names=FALSE) 
# 創(chuàng)建 Boosting 樹模型 # 
repalceNAsWithMean <- function(x) {replace(x, is.na(x), mean(x[!is.na(x)]))} 
training <- repalceNAsWithMean(training) 
testing <- repalceNAsWithMean(testing) 
# 重采樣技術(shù) # 
View(train_set) 
fitcontrol<-trainControl(method="repeatedcv",number=10,repeats=1,verbose=FALSE) 
gbmfit<-train(CHURN_FLAG~.,data=balancedData,method="gbm",verbose=FALSE) 
# 為測試數(shù)據(jù)評分 # 
testing$score_Y=predict(gbmfit,newdata=testing,type="prob")[,2] 
testing$score_Y=ifelse(testing$score_Y>0.5,1,0) 
head(testing,n=10) 
write.table(testing,"D:/ Upasana/RareEvent /testing.txt", sep="\t", row.names=FALSE) 
pred_GBM<-prediction(testing$score_Y,testing$CHURN_FLAG) 
# 模型的表現(xiàn) # 
model_perf_GBM <- performance(pred_GBM, "tpr", "fpr") 
model_perf_GBM1 <- performance(pred_GBM, "tpr", "fpr") 
model_perf_GBM 
pred_GBM1<-as.data.frame(model_perf_GBM) 
auc.tmp_GBM <- performance(pred_GBM,"auc") 
AUC_GBM <- as.numeric(auc.tmp_GBM@y.values) 
auc.tmp_GBM

結(jié)果

這個在平衡數(shù)據(jù)集上使用了 SMOTE 并訓(xùn)練了一個 gradient boosting 算法的平衡數(shù)據(jù)集的辦法能夠顯著改善預(yù)測模型的準(zhǔn)確度。較之平常分析建模技術(shù)(比如 logistic 回歸和決策樹)，這個辦法將其 lift 提升了 20%，精確率也提升了 3 到 4 倍。

四、結(jié)論

遇到不平衡數(shù)據(jù)集時，沒有改善預(yù)測模型準(zhǔn)確性的一站式解決方案。你可能需要嘗試多個辦法來搞清楚最適合數(shù)據(jù)集的采樣技術(shù)。在絕大多數(shù)情況下，諸如 SMOTE 以及 MSMOTE 之類的合成技術(shù)會比傳統(tǒng)過采樣或欠采樣的辦法要好。

為了獲得更好的結(jié)果，你可以在使用諸如 Gradeint boosting 和 XGBoost 的同時也使用 SMOTE 和 MSMOTE 等合成采樣技術(shù)。

通常用于解決不平衡數(shù)據(jù)集問題的先進(jìn) bagging 技術(shù)之一是 SMOTE bagging。這個辦法采取了一種完全不同于傳統(tǒng) bagging 技術(shù)的辦法來創(chuàng)造每個 Bag/Bootstrap。通過每次迭代時設(shè)置一個 SMOTE 重采樣率，它可以借由 SMOTE 算法生成正例。每次迭代時，負(fù)例集會被 bootstrap。

不平衡數(shù)據(jù)集的特點(diǎn)不同，最有效的技術(shù)也會有所不同。對比模型時要考慮相關(guān)評估參數(shù)。

在對比通過全面地結(jié)合上述技術(shù)而構(gòu)建的多個預(yù)測模型時，ROC 曲線下的 Lift & Area 將會在決定最優(yōu)模型上發(fā)揮作用。

本文作者為來自 KPMG 的數(shù)據(jù)分析顧問 Upasana Mukherjee。

原文地址：https://www.analyticsvidhya.com/blog/2017/03/imbalanced-classification-problem/

【本文是51CTO專欄機(jī)構(gòu)機(jī)器之心的原創(chuàng)譯文，微信公眾號“機(jī)器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文

責(zé)任編輯：趙寧寧來源： 51CTO專欄