中科大聯(lián)合華為諾亞提出Entropy Law,揭秘大模型性能、數據壓縮率以及訓練損失關系
本工作由中科大認知智能全國重點實驗室 IEEE Fellow 陳恩紅團隊與華為諾亞方舟實驗室完成。陳恩紅教授團隊深耕數據挖掘、機器學習領域,在頂級期刊與會議上發(fā)表多篇論文,谷歌學術論文引用超兩萬次。諾亞方舟實驗室是華為公司從事人工智能基礎研究的實驗室,秉持理論研究與應用創(chuàng)新并重的理念,致力于推動人工智能領域的技術創(chuàng)新和發(fā)展。
數據是大語言模型(LLMs)成功的基石,但并非所有數據都有益于模型學習。直覺上,高質量的樣本在教授 LLM 上預期會有更好的效率。因此,現有方法通常專注于基于質量的數據選擇。然而,這些方法中的大多數獨立地評估不同的數據樣本,忽略了樣本之間復雜的組合效應。如圖 1 所示,即使每個樣本質量完美,由于它們的互信息冗余或不一致性,它們的組合可能仍然次優(yōu)。盡管基于質量的子集由所有三個優(yōu)質樣本組成,但它們編碼的知識實際上是冗余和沖突的。相比之下,另一個由幾個相對較低質量但多樣化的樣本組成的數據子集在教授 LLM 方面可能傳達更多信息。因此,基于質量的數據選擇并未完全符合最大化 LLM 知識掌握的目標。
而本文旨在揭示 LLM 性能與數據選擇之間的內在關系。受 LLM 信息壓縮本質的啟發(fā),我們發(fā)現了一條 entropy law,它將 LLM 性能與數據壓縮率和前幾步模型訓練的損失加以聯(lián)系,分別反映了數據集的信息冗余程度和 LLM 對數據集中固有知識的掌握程度。通過理論推導和實證評估,我們發(fā)現模型性能與訓練數據的壓縮率呈負相關,而這通常會產生較低的訓練損失。基于 entropy law 的發(fā)現,我們提出了一種非常高效且通用的數據選擇方法用于訓練 LLM,名為 ZIP,其旨在優(yōu)先選擇低壓縮率的數據子集。ZIP 分多階段、貪心地選擇多樣化的數據,最終獲得一個具有良好多樣性的數據子集。

- 團隊:中科大認知智能全國重點實驗室陳恩紅團隊,華為諾亞方舟實驗室
- 論文鏈接: https://arxiv.org/pdf/2407.06645
- 代碼鏈接: https://github.com/USTC-StarTeam/ZIP
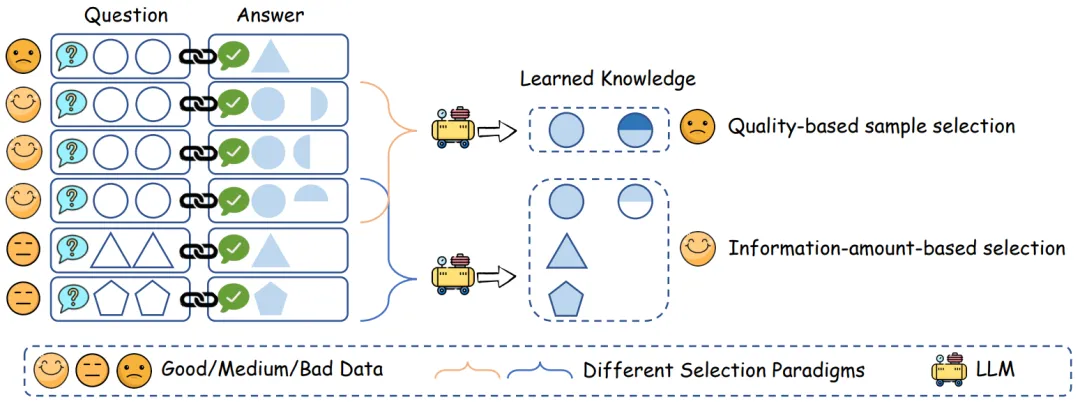
圖 1
Entropy law
我們對數據壓縮與 LLM 性能之間的關系進行理論分析。直覺上,訓練數據的正確性和多樣性會影響最終模型的性能。同時,如果數據存在嚴重的內在沖突或模型對數據編碼的信息掌握不佳,LLM 的性能可能會次優(yōu)。基于這些假設,我們將 LLM 的性能表示為 Z ,其預期會受到以下因素的影響:
- 數據壓縮率 R:直覺上,壓縮率越低的數據集表明信息密度越高。
- 訓練損失 L:表示數據對模型來說是否難以記憶。在相同的基礎模型下,高訓練損失通常是由于數據集中存在噪聲或不一致的信息。
- 數據一致性 C:數據的一致性通過給定前文情況下下一個 token 的概率的熵來反映。更高的數據一致性通常會帶來更低的訓練損失。
- 平均數據質量 Q:反映了數據的平均樣本級質量,可以通過各種客觀和主觀方面來衡量。
給定一定量的訓練數據,模型性能可以通過上述因素來估計:
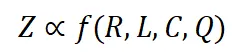
其中 f 是一個隱函數。給定一個特定的基礎模型,L 的規(guī)模通常取決于 R 和 C,可以表示為:
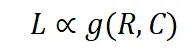
由于具有更高同質性或更好數據一致性的數據集更容易被模型學習,L 預計在 R 和 C 上是單調的。因此,我們可以將上述公式重寫為:
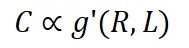
其中 g' 是一個反函數。通過結合上述三個方程,我們得到:
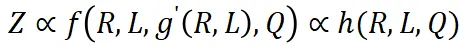
其中 h 是另一個隱函數。如果數據選擇方法不會顯著改變平均數據質量 Q,我們可以近似地將變量 Q 視為常數。因此,最終性能可以粗略地表示為:
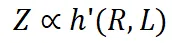
這意味著模型性能與數據壓縮率和訓練損失相關。我們將這種關系稱為 Entropy law。
基于 Entropy law,我們提出兩個推論:
- 如果將 C 視為常數,訓練損失直接受壓縮率影響。因此,模型性能由壓縮率控制:如果數據壓縮率 R 較高,那么 Z 通常較差,這將在我們的實驗中得到驗證。
- 在相同的壓縮率下,較高訓練損失意味著較低的數據一致性。因此,模型學到的有效知識可能更有限。這可以用來預測 LLM 在具有相似壓縮率和樣本質量的不同數據上的性能。我們將在后續(xù)展示這一推論在實踐中的應用。
ZIP:高度輕量化的數據選擇算法
在 entropy law 的指導下,我們提出了 ZIP 這一數據選擇方法,通過數據壓縮率來選擇數據樣本,旨在在有限的訓練數據預算下最大化有效信息量。出于效率考量,我們采用了一種迭代多階段貪心范式,以高效地獲得具有相對低壓縮率的近似解。在每輪迭代中,我們首先使用全局選擇階段來選擇一組具有低壓縮率的候選樣本池,找到信息密度高的樣本。然后,我們采用粗粒度的局部選擇階段,選擇一組與已選樣本冗余度最低的較小樣本集。最后,我們使用細粒度的局部選擇階段,最小化要添加樣本之間的相似性。上述過程持續(xù)進行直到獲得足夠的數據,具體算法如下:

實驗結果
1.ZIP 選擇算法對于不同 LLM、在不同 LLM 對齊階段的有效性
對比不同的 SFT 數據選擇算法,基于 ZIP 選擇數據所訓練得到的模型性能上展現出優(yōu)勢,并且在效率上也占優(yōu)。具體結果見下表:
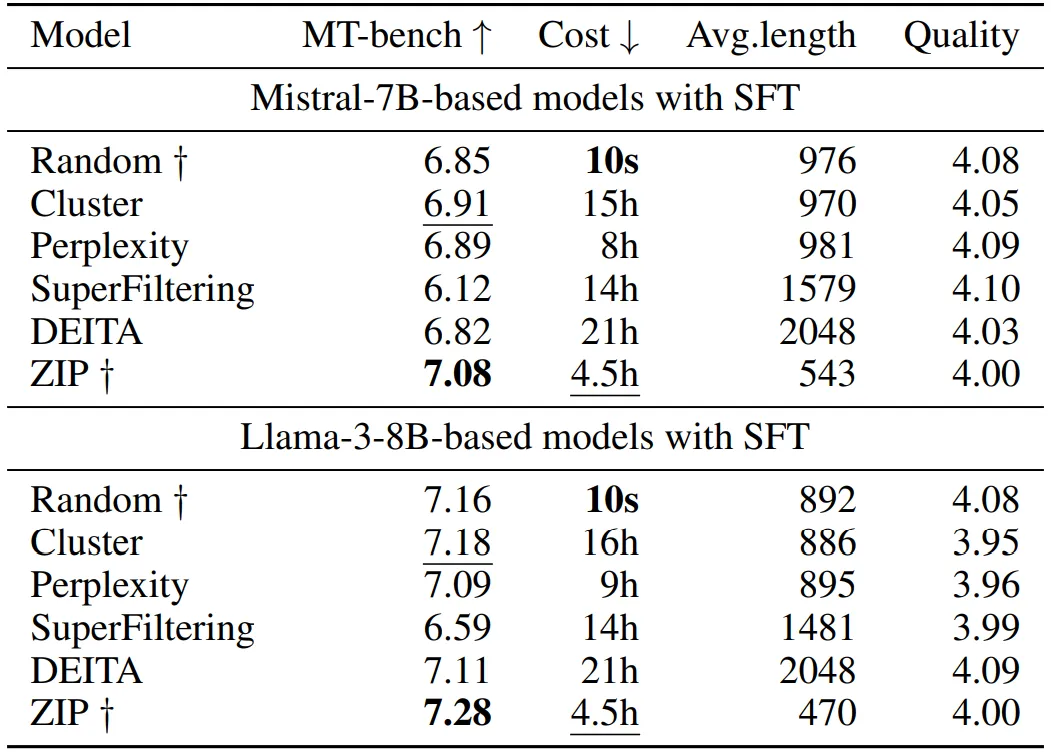
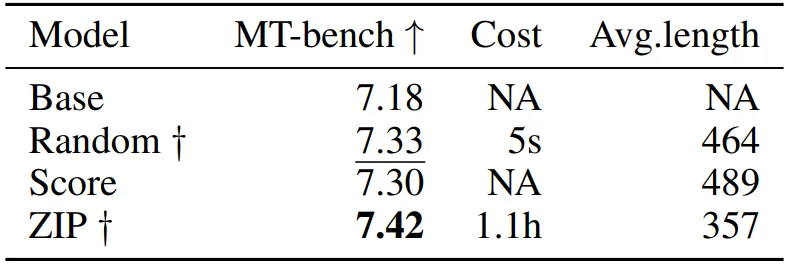
2.Entropy law 的實驗驗證
基于 SFT 數據選擇實驗,我們基于模型效果、數據壓縮率以及模型在前幾步訓練的損失,分別擬合了多條關系曲線。結果見圖 2 以及圖 3,我們從圖中可以觀察到三個因素之間的緊密關聯(lián)。首先,低壓縮率數據通常會帶來更好的模型效果,這是因為 LLMs 的學習過程與信息壓縮高度相關,我們可以將 LLM 視為數據壓縮器,那么壓縮率較低的數據意味著更多的知識量,從而對壓縮器更有價值。同時,可以觀察到較低的壓縮率通常伴隨著更高的訓練損失,這是因為難以壓縮的數據攜帶了更多的知識,對 LLM 吸收其中蘊含的知識提出了更大的挑戰(zhàn)。
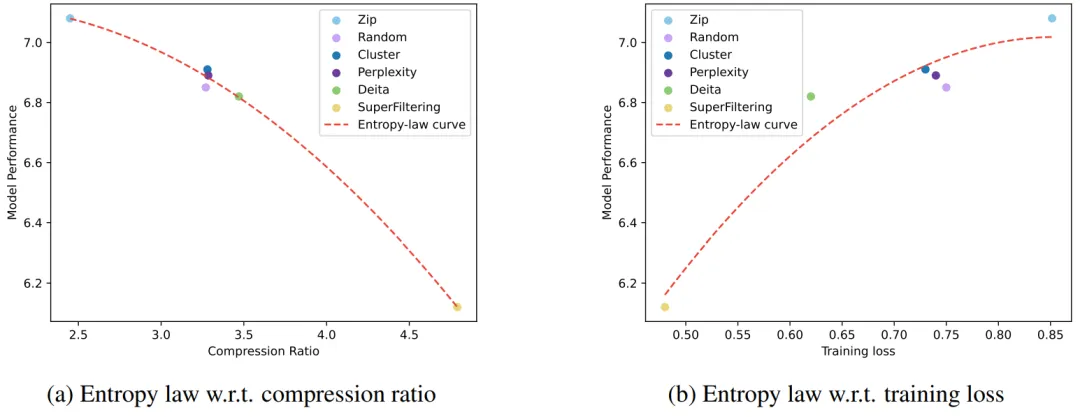
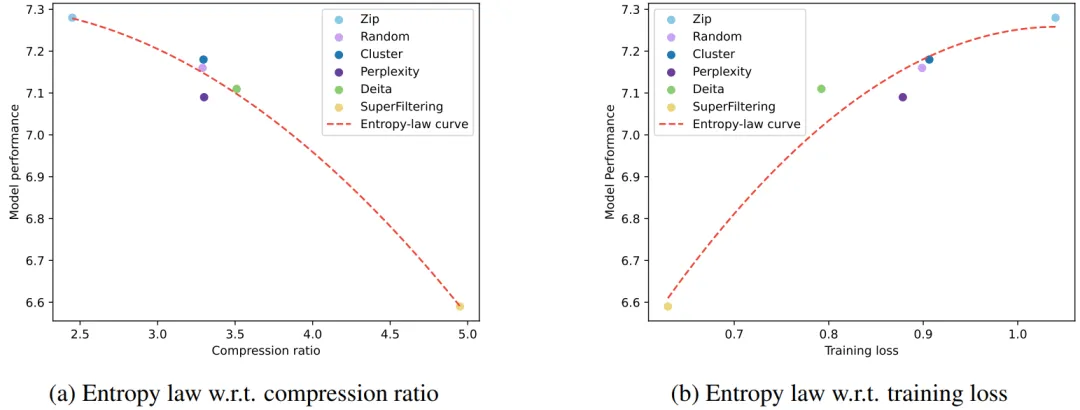
圖 3 Llama-3-8B
3.Entropy law 的實際應用
我們提供了一個 entropy law 在真實場景中指導 LLM 訓練數據增量更新的應用。在該任務場景中,訓練數據量保持相對穩(wěn)定,只有一小部分數據會被修改。結果見圖 4,其中
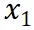
到
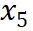
是逐漸增量更新的 5 個數據版本,出于保密要求,僅提供不同壓縮率下模型效果的相對關系。根據 entropy law 預測,假設每次增量更新后數據質量沒有顯著下降,可以預期隨著數據壓縮率的降低,模型性能會有所提升。這一預測與圖中數據版本
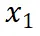
到
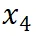
的結果一致。然而,數據版本
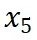
顯示出損失和數據壓縮率的異常增加,這預示了由于訓練數據一致性下降導致的模型性能下降的潛在可能。這一預測通過隨后的模型性能評估進一步得到證實。因此,entropy law 可以作為 LLM 訓練的指導原則,無需在完整數據集上訓練模型直到收斂,便可預測 LLM 訓練失敗的潛在風險。鑒于訓練 LLM 的高昂成本,這一點尤其重要。
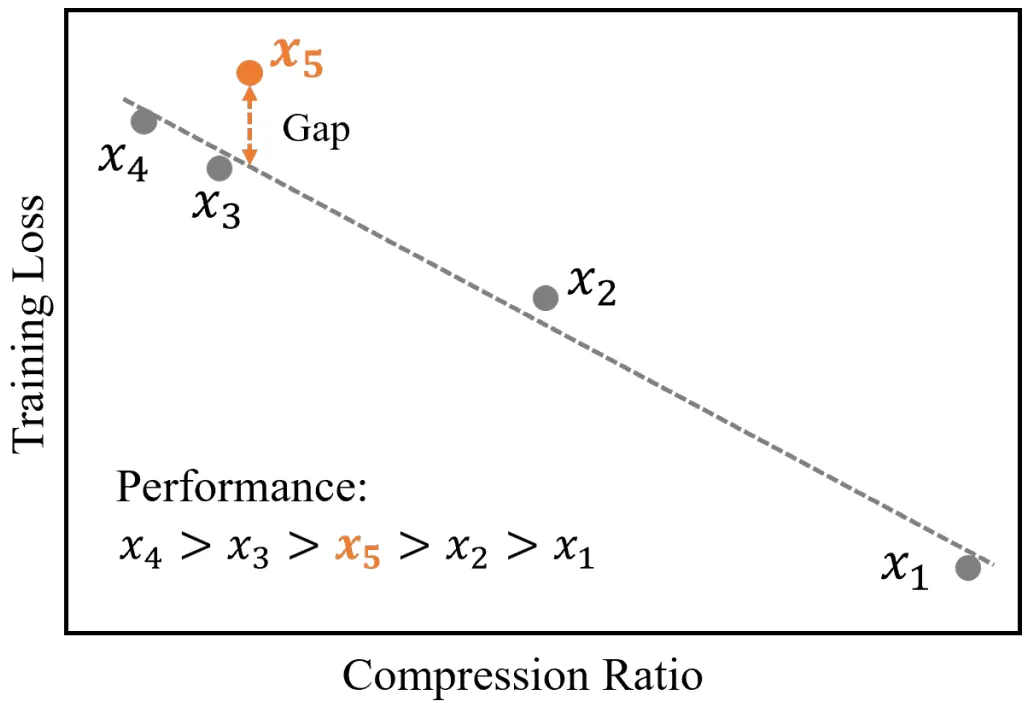
圖 4
本文轉自 機器之心 ,作者:機器之心

















