Friedman 的 h 統計量 (h-stat) 為復雜的機器學習模型提供了一個強大的窗口。具體來說，它可以幫助我們了解它們是否使用交互來進行預測。我們將看到，這種XAI（可解釋性機器學習）方法可以告訴我們一個特征是否與任何其他特征或一個特定特征交互。為此，我們將：

• 使用 Python 包 artemis 應用 h-stat 。
• 解釋輸出，包括交互熱圖和條形圖。

H-stat 是什么？

相互作用是指特征與目標變量之間的關系取決于另一個特征的值。h-stat 通過將兩個或多個特征的聯合部分依賴 (PD) 函數與假設特征不相互作用的聯合 PD 進行比較來量化此相互作用。

重要的一點是，該指標有兩個版本：

• 成對 h-stat — 給出一個特征通過與另一個特征的交互產生的效果的百分比
• 總體 h-stat — 給出某個特征與所有其他特征相互作用所產生的效果的百分比

為了能夠根據特征效果的百分比來解釋指標，我們對它們進行了歸一化。然而，這個過程有時會夸大交互效應。這種情況可能發生在盡管特征的大部分效果來自交互，但整體效果很小的情況下。這就是為什么我們也有這兩個指標的非歸一化版本。當應用該方法時，我們會看到所有這些版本相互補充。

artemis 使用

要應用 H-stat，我們將使用artemis包。這是一個用于分析機器學習模型中交互的有用包。它提供了其他方法，包括 Greenwell 方法和一些特定于模型的方法。

import pandas as pd 
import matplotlib.pyplot as plt 
import random 

from sklearn.ensemble import RandomForestRegressor 
from artemis.interactions_methods.model_agnostic import FriedmanHStatisticMethod

數據和模型

我們將使用鮑魚數據集（https://archive.ics.uci.edu/dataset/1/abalone）來了解 ALE 的工作原理。鮑魚是一種美味的貝類。我們希望使用殼重和去殼重量（肉的重量）等特征來預測其殼中的環數。圖 1顯示了此數據集中所有數值特征的相關性熱圖。你可以看到我們正在處理一些高度相關的特征。

這是一個重要的問題。H -stat 的局限性之一是，當特征實際上高度相關時，它可以識別交互作用。這些被稱為虛假交互作用。隨后我們可以通過使用散點圖確認 h-stat 的結果。

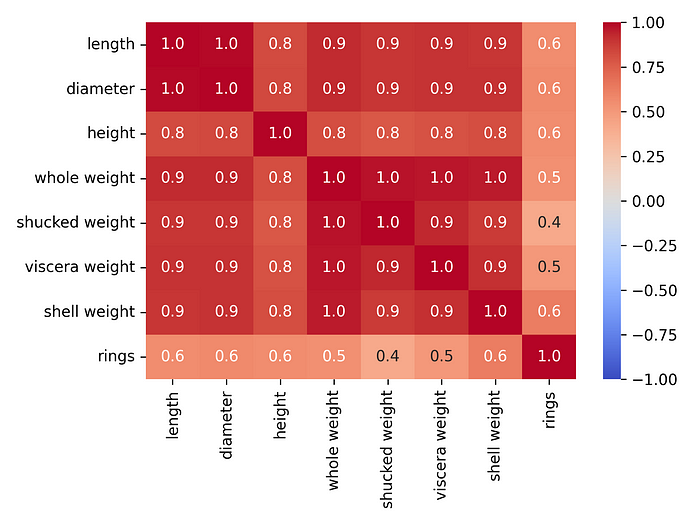圖 1：鮑魚數據集中數值特征的相關性熱圖

我們加載數據集并選擇目標變量。我們還進行了一些特征工程。首先，我們排除一些高度相關的特征。這是因為在圖 1中我們看到它們與其他特征的相關性為 1。最后，我們為性別特征創建獨熱編碼。

#導入數據集
data = pd.read_csv("../../data/abalone.data",
                  names=["sex","length","diameter","height","whole weight",
                         "shucked weight","viscera weight","shell weight","rings"])

y = data["rings"]
X = data[["sex", "length", "height", "shucked weight", "viscera weight", "shell weight"]]

# 創建虛擬變量
X['sex.M'] = [1 if s == 'M' else 0 for s in X['sex']] 
X['sex.F'] = [1 if s == 'F' else 0 for s in X['sex']] 
X['sex.I'] = [1 if s == 'I' else 0 for s in X['sex']]
X = X.drop('sex', axis=1)

X.head()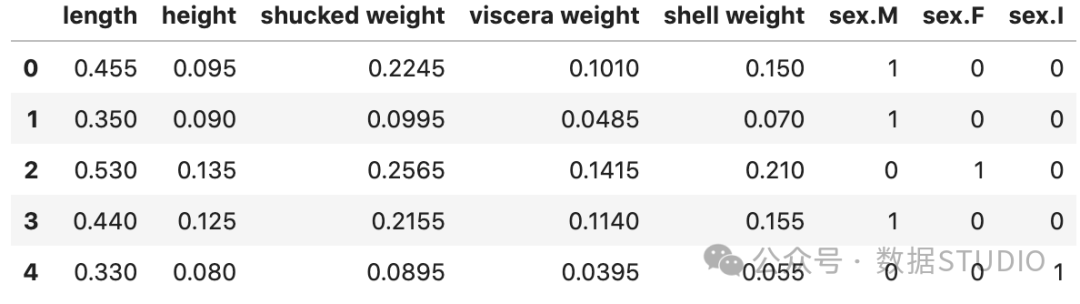

我們使用這些特征來訓練模型來預測環的數量。在本例中，我們使用了隨機森林模型（h-stat 與模型無關，因此這應該能夠將其應用于大多數建模包）。

# 訓練模型
model = RandomForestRegressor() 
model.fit(X, y)

總體H-stat

H-stat 的計算成本很高，很多場景不太適合高維數據集。這里我們首先從特征矩陣中隨機選擇一組 100 個實例，以獲得穩定的指標估計值。

# 隨機選擇 100 個觀測值
random.seed(8) 
X_exp = random.choices(X.to_numpy(), k=100) 
X_exp = pd.DataFrame(X_exp, columns=X.columns)

創建一個 H-stat 對象。然后使用 100 個實例來計算模型的 H-stats。

# 計算 H 統計量
h_stat = FriedmanHStatisticMethod() 
h_stat.fit(model, X_exp)

直接將指標可視化為整體交互的圖。

# 整體交互圖
fig, ax = plt.subplots(figsize=(10 , 5)) 
h_stat.plot(vis_type='bar_chart_ova', ax=ax)

從該圖表中，我們可以看出，殼重和去殼重量的相互作用似乎很顯著（或至少比其他特征更顯著）。殼重對預測環數的影響中約有35% 來自與其他特征的相互作用。對于去殼重量，該值約為27% ，而對于其他特征，該值不到10% 。

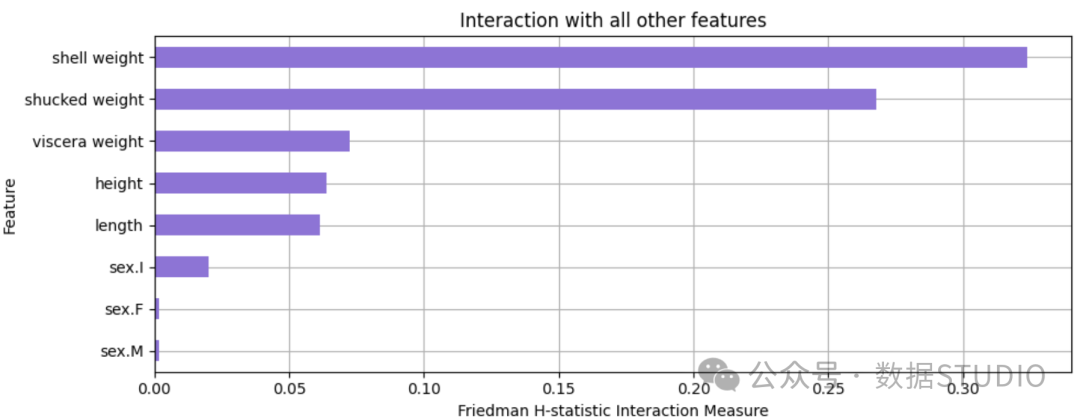圖 3：H 統計量顯示與所有其他特征的相互作用

成對 H-stat

問題是殼重和去殼重量與哪些特征有相互作用？。為此可以使用下面的代碼繪制成對的 H-stat。

# 成對 h-stat
fig, ax = plt.subplots(figsize=( 10 , 4 )) 
h_stat.plot(vis_type='bar_chart', ax=ax)

該圖表明這些特征相互作用。它們的聯合 PDP 中約 24% 的變化來自兩個特征之間的相互作用。長度和內臟重量（length:viscera weigh）之間的相互作用可能也不太顯著。

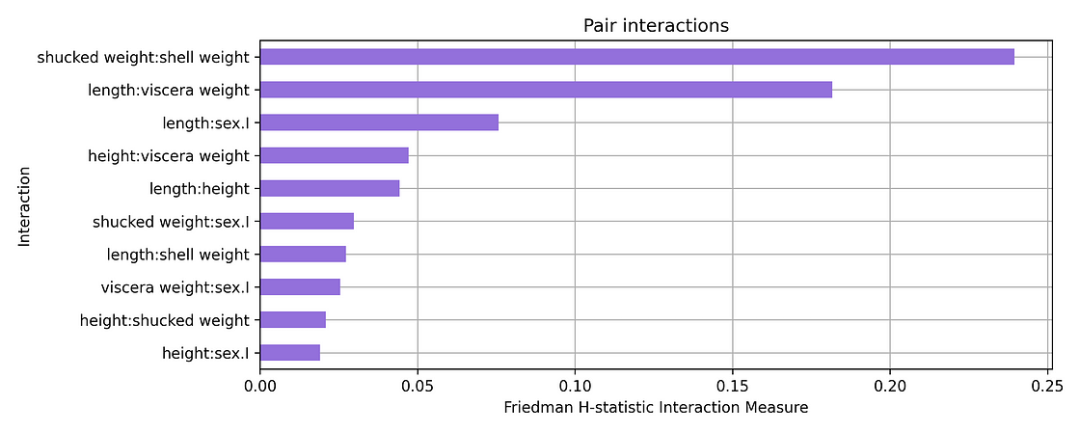圖 4：顯示成對相互作用的 H 統計量的條形圖

更直觀的可視化此信息的方法是使用熱圖（直接設置參數即可）。對角線給出了每個特征的排列特征重要性分數。我們可以看到，不僅這兩個特征（shell weight:shucked weight）的相互作用顯著，而且它們的自身作用也顯著。

# 交互熱圖
h_stat.plot()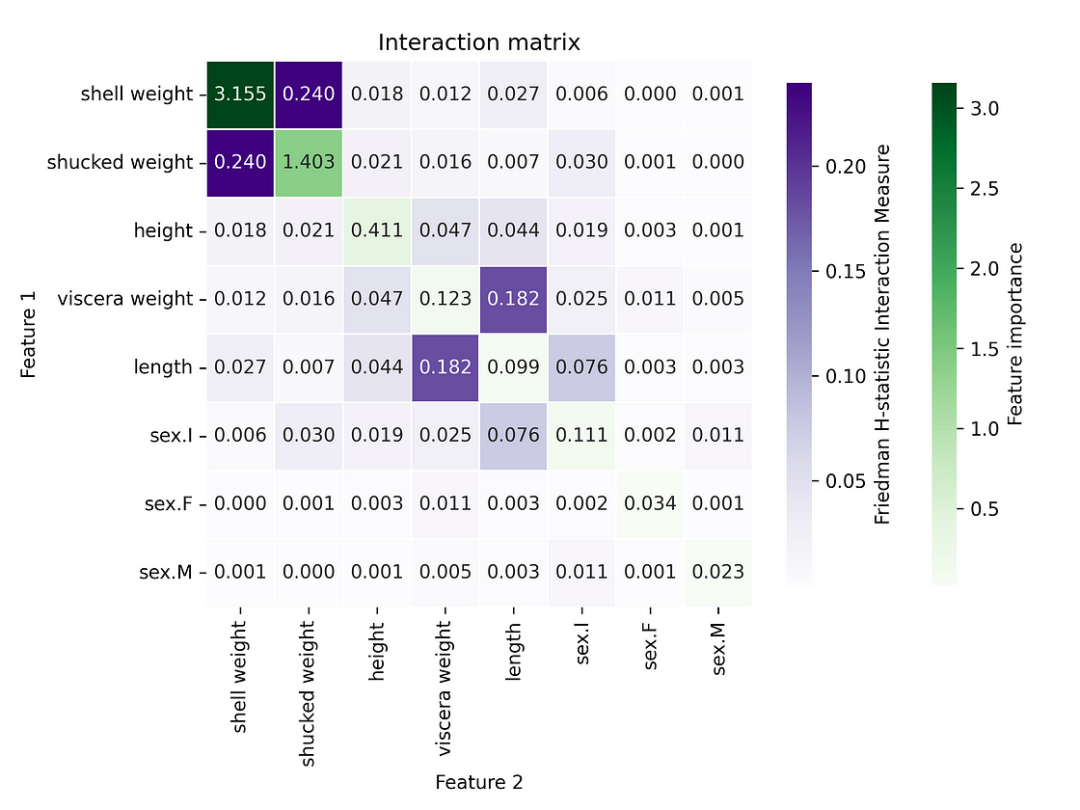

圖 5：H-stat 熱圖顯示成對相互作用

非標準化H-stat

如上所述，通過標準化 H-stat，我們可以夸大一些相互作用。artimise 包可以計算未標準化的值。為此，我們使用與之前相同的代碼，只是我們將 normalized 參數設置為 False。

h_stat_unnormalized = FriedmanHStatisticMethod(normalized= False ) 
h_stat_unnormalized.fit(model, X_exp) 

# 繪制熱圖
h_stat_unnormalized.plot()

交互值不再全部介于 0 和 1 之間。內臟重量和長度（ viscera weight: length）之間的交互似乎不再顯著。所以也許它在之前的圖中被夸大了。

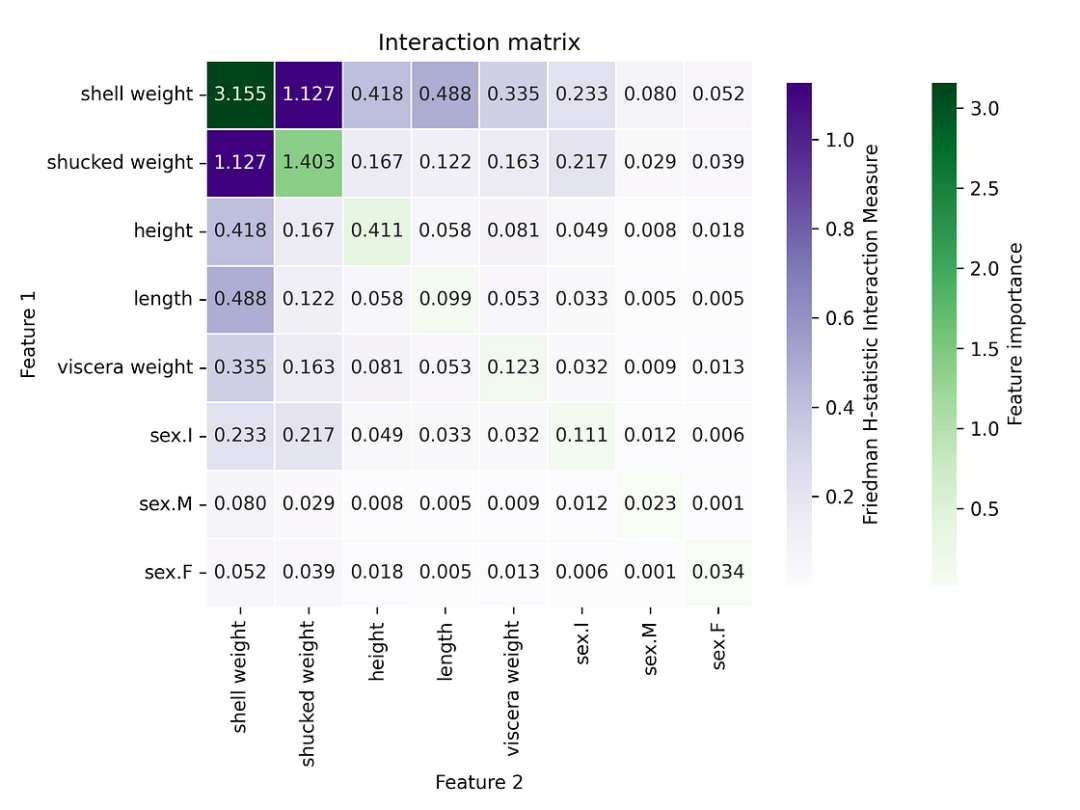圖 6：H 統計量熱圖顯示未標準化的成對相互作用

此時，我們應該考慮H-stat 的另一個弱點——虛假相互作用。在圖 1中，我們看到模型特征都高度相關。因此，我們需要確保 H-stat 不會將多重共線性與相互作用混淆。

一種方法是將底層數據集中的交互可視化。為此，我們創建了殼重與去殼重的散點圖。我們根據環數對點進行著色，并添加顏色條。現在可以清楚地看到這種相互作用的性質。

# 殼重量和去殼重量之間的相互作用
plt.scatter(X["shell weight"], X["shucked weight"], c=y, cmap="bwr")
plt.colorbar(label="Number of Rings", orientatinotallow="vertical")
plt.xlabel("shucked weight", size=15)
plt.ylabel("shell weight", size=15)

我們可以看到，環的數量會隨著去殼重量的增加而增加。同時，當去殼重量（鮑魚肉的重量）相對于鮑魚殼較大時，環的數量也會更多。可能發生的情況是，鮑魚的殼會隨著年齡的增長而增長，在某個時候，它會停止增長。然而，鮑魚肉會繼續增長。這就是為什么我們看到最老的鮑魚肉比鮑魚殼更多。

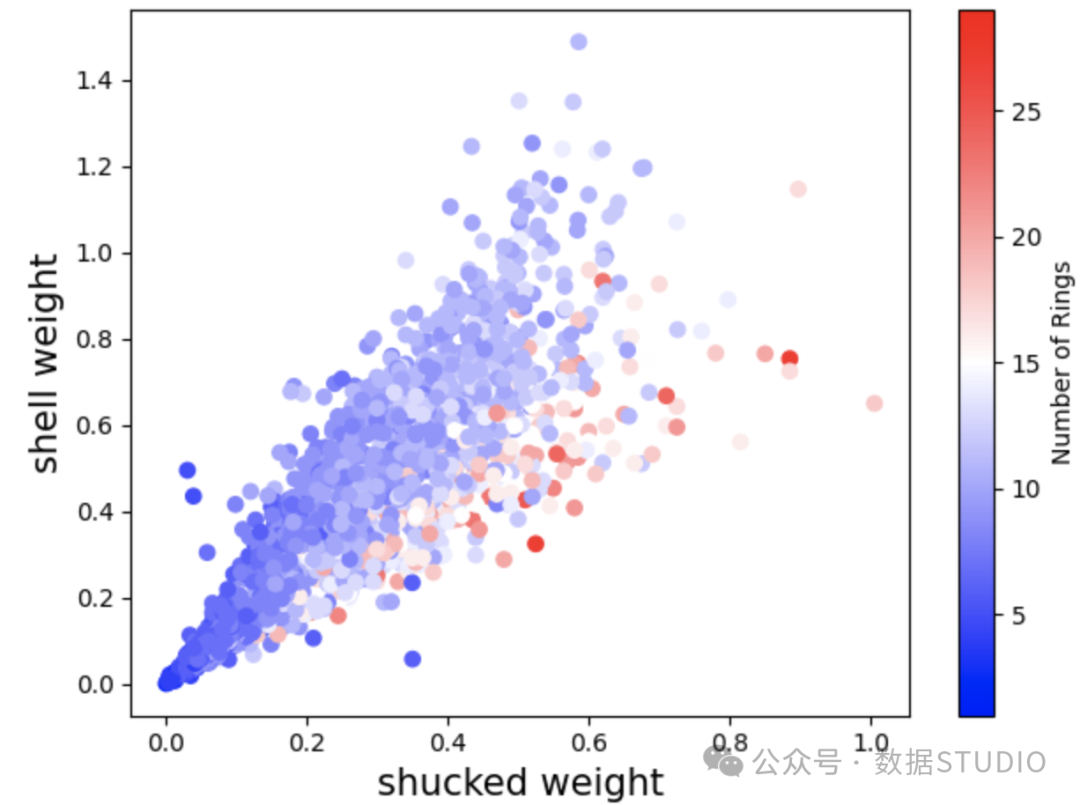圖 7：散點圖顯示殼重和去殼重量之間的相互作用

因此，盡管存在多重共線性，該方法仍然產生了一些有價值的結果。這是一個教訓，雖然你應該避免在模型中包含高度相關的特征，但它們不一定是模型無關方法的終點。你只需使用其他方法驗證結果即可。

我們看到了整體、成對和非標準化 h-stat 如何協同工作，以提供模型中交互的清晰視圖。但是，與所有方法一樣，它們也有其局限性。為了抵消這些局限性，值得應用其他XAI]方法來分析交互。