機(jī)器學(xué)習(xí)模型中特征貢獻(xiàn)度分析:預(yù)測貢獻(xiàn)與錯(cuò)誤貢獻(xiàn)
在機(jī)器學(xué)習(xí)領(lǐng)域,特征重要性分析是一種廣泛應(yīng)用的模型解釋工具。但是特征重要性并不等同于特征質(zhì)量。本文將探討特征重要性與特征有效性之間的關(guān)系,并引入兩個(gè)關(guān)鍵概念:預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度。
核心概念
- 預(yù)測貢獻(xiàn)度:衡量特征在模型預(yù)測中的權(quán)重,反映模型在訓(xùn)練集上識(shí)別的模式。這與傳統(tǒng)的特征重要性概念相似。
- 錯(cuò)誤貢獻(xiàn)度:衡量特征在模型在驗(yàn)證集上產(chǎn)生錯(cuò)誤時(shí)的權(quán)重。這更能反映特征在新數(shù)據(jù)上的泛化能力。
本文將詳細(xì)闡述這兩個(gè)概念的計(jì)算方法,并通過實(shí)例展示基于錯(cuò)誤貢獻(xiàn)度的特征選擇如何優(yōu)于傳統(tǒng)的基于預(yù)測貢獻(xiàn)度的方法。
基礎(chǔ)概念示例
考慮一個(gè)二元分類問題:預(yù)測個(gè)人年收入是否超過10萬美元。假設(shè)我們已有模型預(yù)測結(jié)果:

預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度的計(jì)算主要基于兩個(gè)要素:
- 模型對(duì)每個(gè)樣本的預(yù)測誤差
- 每個(gè)樣本的SHAP(SHapley Additive exPlanations)值
接下來,我們將深入探討這兩個(gè)關(guān)鍵問題:
- 分類模型中應(yīng)采用何種誤差度量?
- 如何處理分類模型中的SHAP值?
分類模型中的錯(cuò)誤度量選擇
在分類模型中,選擇合適的誤差度量至關(guān)重要。我們需要一個(gè)能在樣本級(jí)別計(jì)算并可在整個(gè)數(shù)據(jù)集上聚合的度量指標(biāo)。
對(duì)數(shù)損失(又稱交叉熵)是分類問題中常用的損失函數(shù),其數(shù)學(xué)表達(dá)式如下:
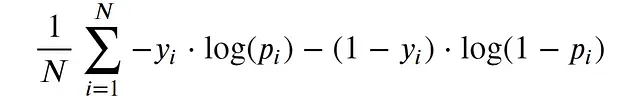
對(duì)數(shù)損失適合我們的需求,因?yàn)椋?/span>
- 公式外部是簡單的平均操作
- 作為損失函數(shù),其值越低越好,符合誤差的概念
為了更直觀地理解對(duì)數(shù)損失,我們可以關(guān)注單個(gè)樣本的貢獻(xiàn):
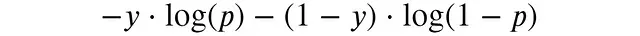
在二元分類問題中,y只能取0或1,因此可以簡化為:
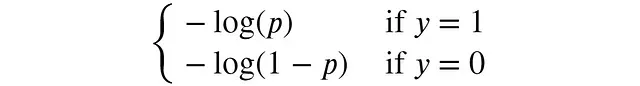
通過可視化可以更好地理解對(duì)數(shù)損失的特性:
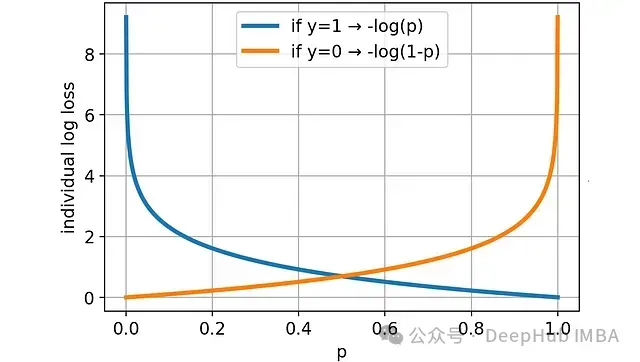
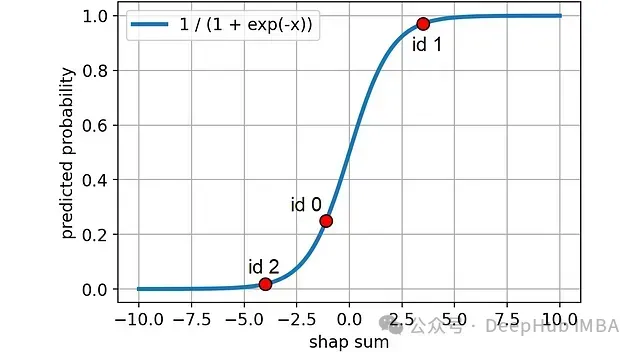
預(yù)測概率越偏離真實(shí)值(0或1),損失越大。且當(dāng)預(yù)測嚴(yán)重偏離時(shí)(如預(yù)測0.2而實(shí)際為1,或預(yù)測0.8而實(shí)際為0),損失增長速度超過線性。
以下是計(jì)算單樣本對(duì)數(shù)損失的Python實(shí)現(xiàn):
def individual_log_loss(y_true, y_pred, eps=1e-15):
"""計(jì)算單個(gè)樣本的對(duì)數(shù)損失"""
y_pred = np.clip(y_pred, eps, 1 - eps)
return -y_true * np.log(y_pred) - (1 - y_true) * np.log(1 - y_pred)應(yīng)用到我們的示例數(shù)據(jù)集:

可以觀察到,樣本1和2的對(duì)數(shù)損失較小,因?yàn)轭A(yù)測接近實(shí)際值;而樣本0的對(duì)數(shù)損失較大。
分類模型中SHAP值的處理方法
在樹模型(如XGBoost、LightGBM和CatBoost)中,計(jì)算SHAP值相對(duì)簡單:
from shap import TreeExplainer
shap_explainer = TreeExplainer(model)
shap_values = shap_explainer.shap_values(X)假設(shè)我們得到以下SHAP值:
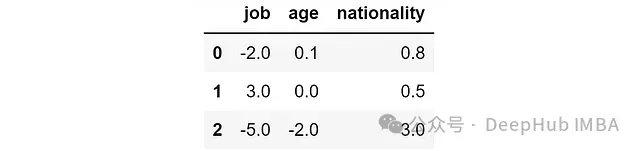
SHAP值的基本解釋:
- 正值表示該特征增加了預(yù)測概率
- 負(fù)值表示該特征降低了預(yù)測概率
SHAP值之和與模型預(yù)測直接相關(guān),但并不等于預(yù)測概率(介于0和1之間)。所以我們需要一個(gè)函數(shù)將SHAP值之和轉(zhuǎn)換為概率,該函數(shù)應(yīng)滿足:
- 將任意實(shí)數(shù)映射到[0,1]區(qū)間
- 嚴(yán)格單調(diào)遞增
Sigmoid函數(shù)滿足這些要求。因此模型對(duì)特定樣本的預(yù)測概率等于該樣本SHAP值之和的Sigmoid函數(shù)值。
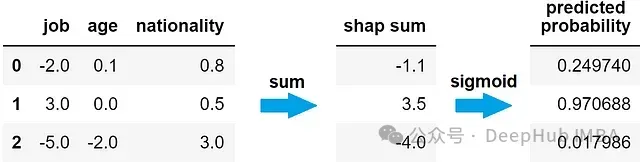
Sigmoid函數(shù)圖像:
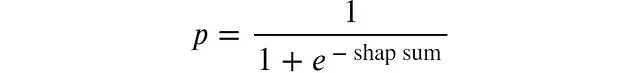
Python實(shí)現(xiàn):
def shap_sum2proba(shap_sum):
"""將SHAP值之和轉(zhuǎn)換為預(yù)測概率"""
return 1 / (1 + np.exp(-shap_sum))下圖示例中的樣本在Sigmoid曲線上的位置:
接下來,我們將詳細(xì)討論預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度的計(jì)算方法。
預(yù)測貢獻(xiàn)度的計(jì)算
預(yù)測貢獻(xiàn)度反映了特征對(duì)模型最終預(yù)測的影響程度。當(dāng)一個(gè)特征的SHAP值絕對(duì)值較大時(shí),表明該特征對(duì)預(yù)測結(jié)果有顯著影響。因此可以通過計(jì)算特征SHAP值的絕對(duì)值平均來量化預(yù)測貢獻(xiàn)度。
實(shí)現(xiàn)代碼如下:
prediction_contribution = shap_values.abs().mean()應(yīng)用到我們的示例數(shù)據(jù)集,得到以下結(jié)果:

從結(jié)果可以看出,就特征重要性而言,job是最主要的特征,其次是nationality,然后是age。
錯(cuò)誤貢獻(xiàn)度的計(jì)算
錯(cuò)誤貢獻(xiàn)度旨在評(píng)估移除某個(gè)特征后模型錯(cuò)誤的變化。利用SHAP值,我們可以模擬特征缺失的情況:從SHAP值總和中減去特定特征的SHAP值,然后應(yīng)用Sigmoid函數(shù),即可得到模型在缺少該特征時(shí)的預(yù)測概率。
實(shí)現(xiàn)代碼如下:
y_pred_wo_feature = shap_values.apply(lambda feature: shap_values.sum(axis=1) - feature).applymap(shap_sum2proba)應(yīng)用到示例數(shù)據(jù)集的結(jié)果:
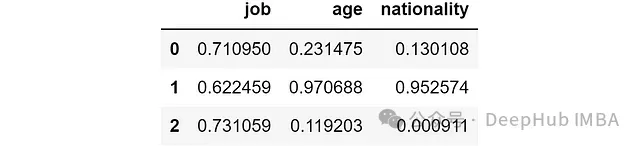
解讀結(jié)果:
- 如果沒有job特征,模型對(duì)三個(gè)樣本的預(yù)測概率分別為71%、62%和73%。
- 如果沒有nationality特征,預(yù)測概率分別為13%、95%和0%。
可以看出,預(yù)測結(jié)果對(duì)特征的依賴程度各不相同。接下來我們計(jì)算移除特征后的對(duì)數(shù)損失:
ind_log_loss_wo_feature = y_pred_wo_feature.apply(lambda feature: individual_log_loss(y_true=y_true, y_pred=feature))結(jié)果如下:
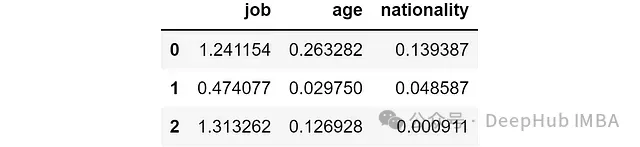
對(duì)第一個(gè)樣本而言,移除job特征會(huì)導(dǎo)致對(duì)數(shù)損失增加到1.24,而移除nationality特征只會(huì)使對(duì)數(shù)損失增加到0.13。
為了評(píng)估特征的影響,我們可以計(jì)算完整模型的對(duì)數(shù)損失與移除特征后對(duì)數(shù)損失的差值:
ind_log_loss = individual_log_loss(y_true=y_true, y_pred=y_pred)
ind_log_loss_diff = ind_log_loss_wo_feature.apply(lambda feature: ind_log_loss - feature)結(jié)果如下:
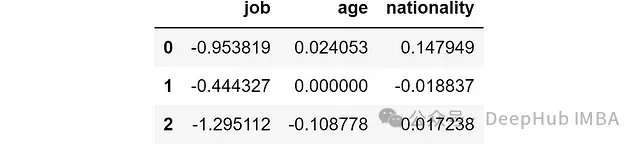
結(jié)果解讀如下:
- 負(fù)值表示特征的存在減少了預(yù)測錯(cuò)誤,對(duì)該樣本有積極影響。
- 正值表示特征的存在增加了預(yù)測錯(cuò)誤,對(duì)該樣本有消極影響。
最后計(jì)算每個(gè)特征的錯(cuò)誤貢獻(xiàn)度,即這些差值的平均值:
error_contribution = ind_log_loss_diff.mean()結(jié)果如下:

結(jié)果解讀:
- 負(fù)值表示特征總體上有積極影響,減少了模型的平均錯(cuò)誤。
- 正值表示特征總體上有消極影響,增加了模型的平均錯(cuò)誤。
在這個(gè)例子中,job特征的存在平均減少了0.897的對(duì)數(shù)損失,而nationality特征的存在平均增加了0.049的對(duì)數(shù)損失。盡管nationality是第二重要的特征(根據(jù)預(yù)測貢獻(xiàn)度),但它實(shí)際上略微降低了模型性能。
實(shí)際數(shù)據(jù)集應(yīng)用案例
我們將使用一個(gè)名為"Gold"的金融時(shí)間序列數(shù)據(jù)集來演示這些概念的實(shí)際應(yīng)用。該數(shù)據(jù)集來源于Pycaret庫。
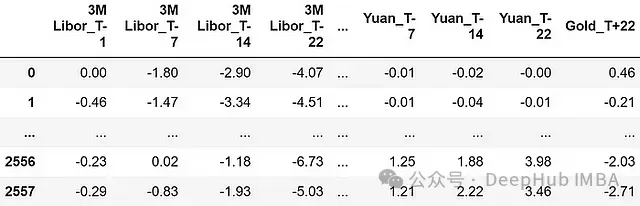
特征說明:
- 所有特征都表示為百分比回報(bào)率
- 特征包括金融資產(chǎn)在觀察時(shí)刻前22、14、7和1天的回報(bào)率(分別標(biāo)記為"T-22"、"T-14"、"T-7"、"T-1")
完整的預(yù)測特征列表如下:

總共有120個(gè)特征。
預(yù)測目標(biāo):預(yù)測22天后黃金回報(bào)率是否會(huì)超過5%。因此,這是一個(gè)二元分類問題:
- 0:22天后黃金回報(bào)率小于或等于5%
- 1:22天后黃金回報(bào)率大于5%
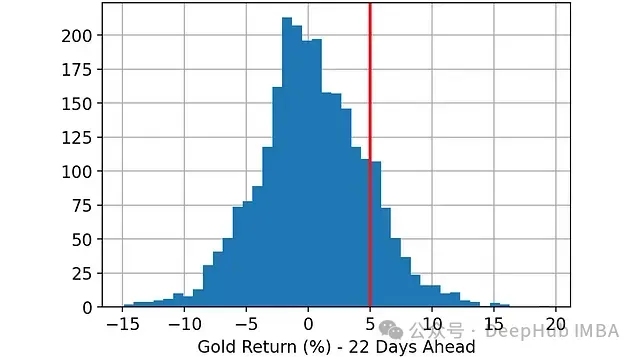
實(shí)驗(yàn)步驟:
- 隨機(jī)劃分?jǐn)?shù)據(jù)集:33%用于訓(xùn)練,33%用于驗(yàn)證,34%用于測試。
- 使用訓(xùn)練集訓(xùn)練LightGBM分類器。
- 在訓(xùn)練、驗(yàn)證和測試集上進(jìn)行預(yù)測。
- 使用SHAP庫計(jì)算各數(shù)據(jù)集的SHAP值。
- 計(jì)算每個(gè)特征在各數(shù)據(jù)集上的預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度。
分析結(jié)果:
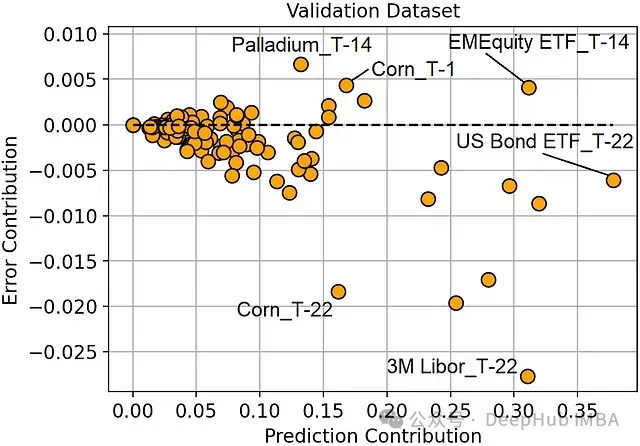 圖:驗(yàn)證集上的預(yù)測貢獻(xiàn)度vs錯(cuò)誤貢獻(xiàn)度
圖:驗(yàn)證集上的預(yù)測貢獻(xiàn)度vs錯(cuò)誤貢獻(xiàn)度
主要發(fā)現(xiàn):
- 美國債券ETF在T-22時(shí)點(diǎn)是最重要的特征,但它并未帶來顯著的錯(cuò)誤減少。
- 3個(gè)月Libor在T-22時(shí)點(diǎn)是最有效的特征,因?yàn)樗畲蟪潭鹊販p少了錯(cuò)誤。
- 玉米價(jià)格在T-1和T-22時(shí)點(diǎn)都是重要特征,但T-1時(shí)點(diǎn)的特征存在過擬合現(xiàn)象(增加了預(yù)測錯(cuò)誤)。
- 總體而言,T-1或T-14時(shí)點(diǎn)的特征錯(cuò)誤貢獻(xiàn)度較高,而T-22時(shí)點(diǎn)的特征錯(cuò)誤貢獻(xiàn)度較低。這表明較近期的特征可能更容易導(dǎo)致過擬合,而較早期的特征可能具有更好的泛化能力。
這些發(fā)現(xiàn)為我們提供了寶貴的模型洞察,并為特征選擇提供了新的思路。下一節(jié)我們將探討如何利用錯(cuò)誤貢獻(xiàn)度進(jìn)行特征選擇。
驗(yàn)證:基于錯(cuò)誤貢獻(xiàn)度的遞歸特征消除
遞歸特征消除(Recursive Feature Elimination,RFE)是一種迭代式特征選擇方法,通過逐步移除特征來優(yōu)化模型性能。本節(jié)將比較基于預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度的RFE方法。
RFE算法概述:
- 初始化特征集
- 使用當(dāng)前特征集訓(xùn)練模型
- 評(píng)估各特征的重要性或貢獻(xiàn)度
- 移除"最差"特征
- 重復(fù)步驟2-4,直到達(dá)到預(yù)定的特征數(shù)量或性能標(biāo)準(zhǔn)
傳統(tǒng)RFE vs. 基于錯(cuò)誤貢獻(xiàn)度的RFE:
- 傳統(tǒng)RFE:移除預(yù)測貢獻(xiàn)度最低的特征
- 基于錯(cuò)誤貢獻(xiàn)度的RFE:移除錯(cuò)誤貢獻(xiàn)度最高的特征
實(shí)驗(yàn)結(jié)果
驗(yàn)證集上的對(duì)數(shù)損失比較:
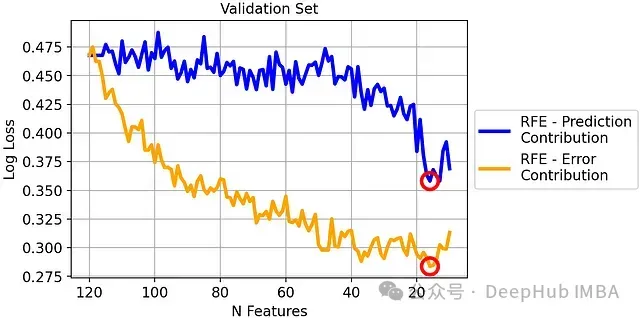
基于錯(cuò)誤貢獻(xiàn)度的RFE在驗(yàn)證集上顯著優(yōu)于傳統(tǒng)RFE。
測試集上的對(duì)數(shù)損失比較:
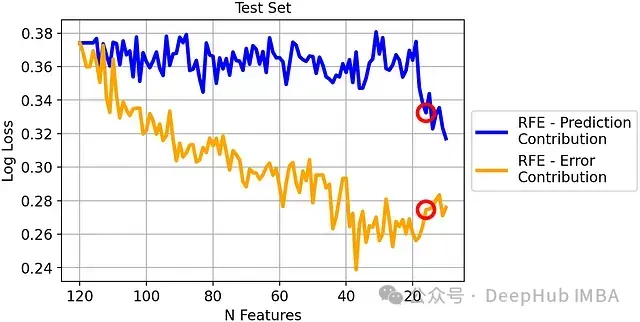
盡管差異相對(duì)減小,但基于錯(cuò)誤貢獻(xiàn)度的RFE在測試集上仍然優(yōu)于傳統(tǒng)RFE,證明了其更好的泛化能力。
驗(yàn)證集上的平均精度比較:
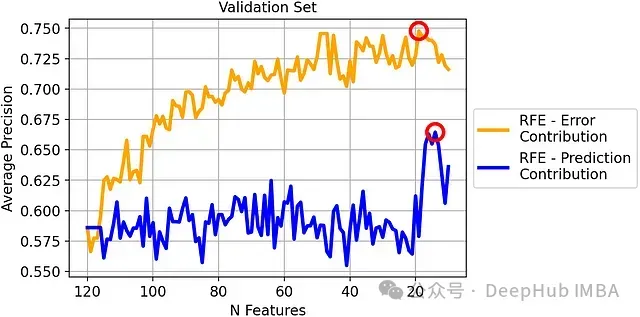
盡管錯(cuò)誤貢獻(xiàn)度是基于對(duì)數(shù)損失計(jì)算的,但在平均精度這一不同的評(píng)估指標(biāo)上,基于錯(cuò)誤貢獻(xiàn)度的RFE仍然表現(xiàn)出色。
根據(jù)驗(yàn)證集性能,我們選擇:
- 基于錯(cuò)誤貢獻(xiàn)度的RFE:19個(gè)特征的模型
- 基于預(yù)測貢獻(xiàn)度的RFE:14個(gè)特征的模型
測試集上的平均精度比較:
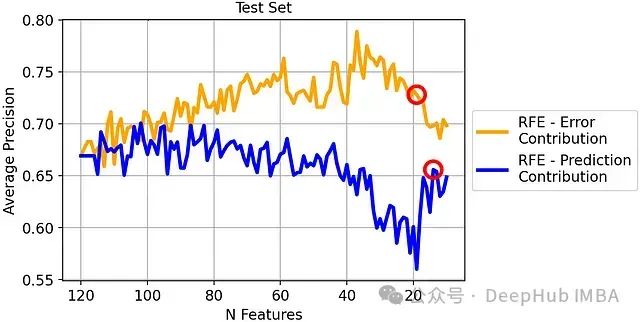
最終結(jié)果:
- 基于錯(cuò)誤貢獻(xiàn)度的RFE(19個(gè)特征):72.8%的平均精度
- 基于預(yù)測貢獻(xiàn)度的RFE(14個(gè)特征):65.6%的平均精度
基于錯(cuò)誤貢獻(xiàn)度的RFE在測試集上獲得了7.2個(gè)百分點(diǎn)的性能提升,這是一個(gè)顯著的改進(jìn)。
總結(jié)
本研究深入探討了機(jī)器學(xué)習(xí)模型中特征重要性的概念,并提出了區(qū)分特征重要性和特征有效性的新方法。
- 引入了預(yù)測貢獻(xiàn)度和錯(cuò)誤貢獻(xiàn)度兩個(gè)概念,為特征評(píng)估提供了新的視角。
- 詳細(xì)闡述了基于SHAP值計(jì)算這兩種貢獻(xiàn)度的方法,為實(shí)踐應(yīng)用提供了可操作的指導(dǎo)。
- 通過金融數(shù)據(jù)集的案例分析,展示了錯(cuò)誤貢獻(xiàn)度在特征選擇中的實(shí)際應(yīng)用價(jià)值。
- 證明了基于錯(cuò)誤貢獻(xiàn)度的遞歸特征消除方法可以顯著提高模型性能,在測試集上實(shí)現(xiàn)了7.2%的平均精度提升。
通過深入理解特征的預(yù)測貢獻(xiàn)和錯(cuò)誤貢獻(xiàn),數(shù)據(jù)科學(xué)家可以構(gòu)建更加穩(wěn)健和高效的機(jī)器學(xué)習(xí)模型,為決策制定提供更可靠的支持。