多層感知器（MLP），也被稱為全連接前饋神經(jīng)網(wǎng)絡(luò)，是當(dāng)今深度學(xué)習(xí)模型的基礎(chǔ)構(gòu)建塊。MLP 的重要性無(wú)論怎樣強(qiáng)調(diào)都不為過(guò)，因?yàn)樗鼈兪菣C(jī)器學(xué)習(xí)中用于逼近非線性函數(shù)的默認(rèn)方法。

但是最近，來(lái)自 MIT 等機(jī)構(gòu)的研究者提出了一種非常有潛力的替代方法 ——KAN。該方法在準(zhǔn)確性和可解釋性方面表現(xiàn)優(yōu)于 MLP。而且，它能以非常少的參數(shù)量勝過(guò)以更大參數(shù)量運(yùn)行的 MLP。比如，作者表示，他們用 KAN 重新發(fā)現(xiàn)了結(jié)理論中的數(shù)學(xué)規(guī)律，以更小的網(wǎng)絡(luò)和更高的自動(dòng)化程度重現(xiàn)了 DeepMind 的結(jié)果。具體來(lái)說(shuō)，DeepMind 的 MLP 有大約 300000 個(gè)參數(shù)，而 KAN 只有大約 200 個(gè)參數(shù)。

這些驚人的結(jié)果讓 KAN 迅速走紅，吸引了很多人對(duì)其展開(kāi)研究。很快，有人提出了一些質(zhì)疑。其中，一篇標(biāo)題為《KAN is just MLP》的 Colab 文檔成為了議論的焦點(diǎn)。

KAN 只是一個(gè)普通的 MLP？   

上述文檔的作者表示，你可以把 KAN 寫成一個(gè) MLP，只要在 ReLU 之前加一些重復(fù)和移位。

在一個(gè)簡(jiǎn)短的例子中，作者展示了如何將 KAN 網(wǎng)絡(luò)改寫為具有相同數(shù)量參數(shù)的、有輕微的非典型結(jié)構(gòu)的普通 MLP。

需要記住的是，KAN 在邊上有激活函數(shù)。它們使用 B - 樣條。在展示的例子中，為了簡(jiǎn)單起見(jiàn)，作者將只使用 piece-wise 線性函數(shù)。這不會(huì)改變網(wǎng)絡(luò)的建模能力。

下面是 piece-wise 線性函數(shù)的一個(gè)例子：

def f(x):
  if x < 0:
    return -2*x
  if x < 1:
    return -0.5*x
  return 2*x - 2.5


X = torch.linspace(-2, 2, 100)
plt.plot(X, [f(x) for x in X])
plt.grid()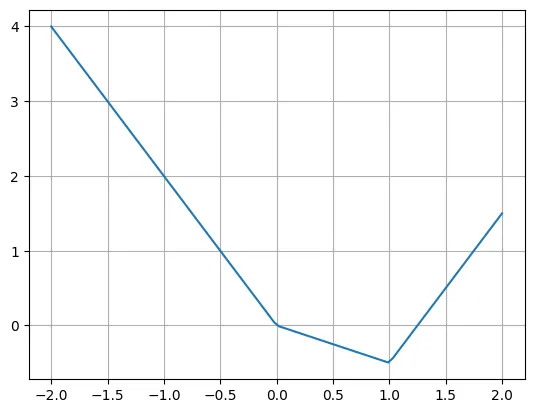

作者表示，我們可以使用多個(gè) ReLU 和線性函數(shù)輕松重寫這個(gè)函數(shù)。請(qǐng)注意，有時(shí)需要移動(dòng) ReLU 的輸入。

plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)
plt.grid()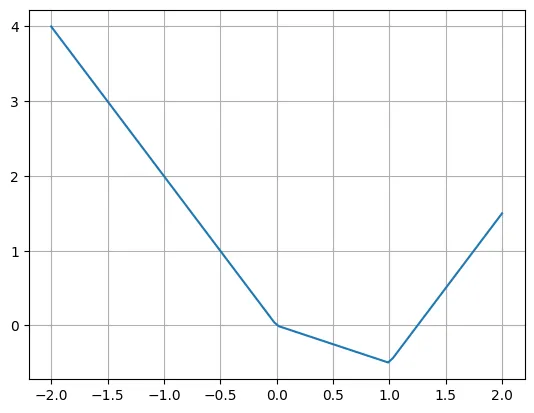

真正的問(wèn)題是如何將 KAN 層改寫成典型的 MLP 層。假設(shè)有 n 個(gè)輸入神經(jīng)元，m 個(gè)輸出神經(jīng)元，piece-wise 函數(shù)有 k 個(gè) piece。這需要 n?m?k 個(gè)參數(shù)（每條邊有 k 個(gè)參數(shù)，而你有 n?m 條邊）。

現(xiàn)在考慮一個(gè) KAN 邊。為此，需要將輸入復(fù)制 k 次，每個(gè)副本移動(dòng)一個(gè)常數(shù)，然后通過(guò) ReLU 和線性層（第一層除外）運(yùn)行。從圖形上看是這樣的（C 是常數(shù)，W 是權(quán)重）：

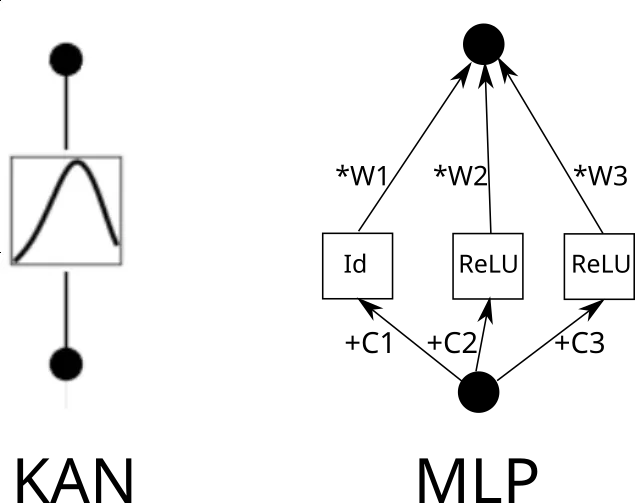
現(xiàn)在，可以對(duì)每一條邊重復(fù)這一過(guò)程。但要注意一點(diǎn)，如果各處的 piece-wise 線性函數(shù)網(wǎng)格相同，我們就可以共享中間的 ReLU 輸出，只需在其上混合權(quán)重即可。就像這樣：

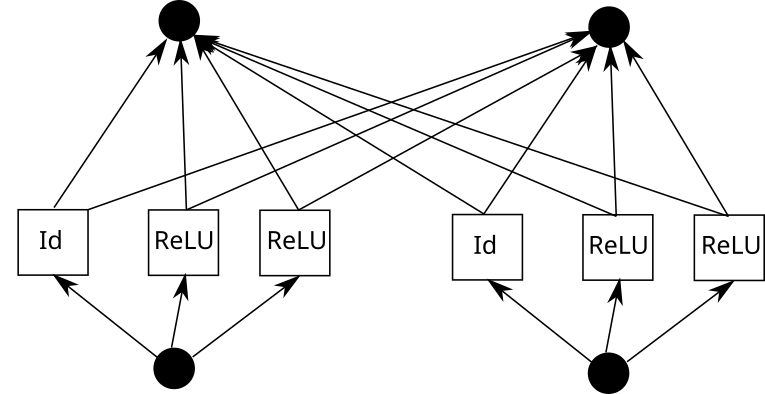
在 Pytorch 中，這可以翻譯成以下內(nèi)容：

k = 3 # Grid size
inp_size = 5
out_size = 7
batch_size = 10
X = torch.randn(batch_size, inp_size) # Our input
linear = nn.Linear(inp_size*k, out_size)  # Weights
repeated = X.unsqueeze(1).repeat(1,k,1)
shifts = torch.linspace(-1, 1, k).reshape(1,k,1)
shifted = repeated + shifts
intermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)
outputs = linear(intermediate)

現(xiàn)在我們的層看起來(lái)是這樣的： 

• Expand + shift + ReLU
• Linear

一個(gè)接一個(gè)地考慮三個(gè)層：

• Expand + shift + ReLU (第 1 層從這里開(kāi)始)
• Linear
• Expand + shift + ReLU (第 2 層從這里開(kāi)始)
• Linear
• Expand + shift + ReLU (第 3 層從這里開(kāi)始)
• Linear

忽略輸入 expansion，我們可以重新排列：

• Linear (第 1 層從這里開(kāi)始)
• Expand + shift + ReLU
• Linear (第 2 層從這里開(kāi)始)
• Expand + shift + ReLU

如下的層基本上可以稱為 MLP。你也可以把線性層做大，去掉 expand 和 shift，獲得更好的建模能力（盡管需要付出更高的參數(shù)代價(jià)）。

• Linear (第 2 層從這里開(kāi)始)
• Expand + shift + ReLU

通過(guò)這個(gè)例子，作者表明，KAN 就是一種 MLP。這一說(shuō)法引發(fā)了大家對(duì)兩類方法的重新思考。

對(duì) KAN 思路、方法、結(jié)果的重新審視

其實(shí)，除了與 MLP 理不清的關(guān)系，KAN 還受到了其他許多方面的質(zhì)疑。

總結(jié)下來(lái)，研究者們的討論主要集中在如下幾點(diǎn)。

第一，KAN 的主要貢獻(xiàn)在于可解釋性，而不在于擴(kuò)展速度、準(zhǔn)確性等部分。

論文作者曾經(jīng)表示：

1. KAN 的擴(kuò)展速度比 MLP 更快。KAN 比參數(shù)較少的 MLP 具有更好的準(zhǔn)確性。
2. KAN 可以直觀地可視化。KAN 提供了 MLP 無(wú)法提供的可解釋性和交互性。我們可以使用 KAN 潛在地發(fā)現(xiàn)新的科學(xué)定律。

其中，網(wǎng)絡(luò)的可解釋性對(duì)于模型解決現(xiàn)實(shí)問(wèn)題的重要性不言而喻：

但問(wèn)題在于：「我認(rèn)為他們的主張只是它學(xué)得更快并且具有可解釋性，而不是其他東西。如果 KAN 的參數(shù)比等效的 NN 少得多，則前者是有意義的。我仍然感覺(jué)訓(xùn)練 KAN 非常不穩(wěn)定。」

那么 KAN 究竟能不能做到參數(shù)比等效的 NN 少很多呢？

這種說(shuō)法目前還存在疑問(wèn)。在論文中，KAN 的作者表示，他們僅用 200 個(gè)參數(shù)的 KAN，就能復(fù)現(xiàn) DeepMind 用 30 萬(wàn)參數(shù)的 MLP 發(fā)現(xiàn)數(shù)學(xué)定理研究。在看到該結(jié)果后，佐治亞理工副教授 Humphrey Shi 的兩位學(xué)生重新審視了 DeepMind 的實(shí)驗(yàn)，發(fā)現(xiàn)只需 122 個(gè)參數(shù)，DeepMind 的 MLP 就能媲美 KAN 81.6% 的準(zhǔn)確率。而且，他們沒(méi)有對(duì) DeepMind 代碼進(jìn)行任何重大修改。為了實(shí)現(xiàn)這個(gè)結(jié)果，他們只減小了網(wǎng)絡(luò)大小，使用隨機(jī)種子，并增加了訓(xùn)練時(shí)間。

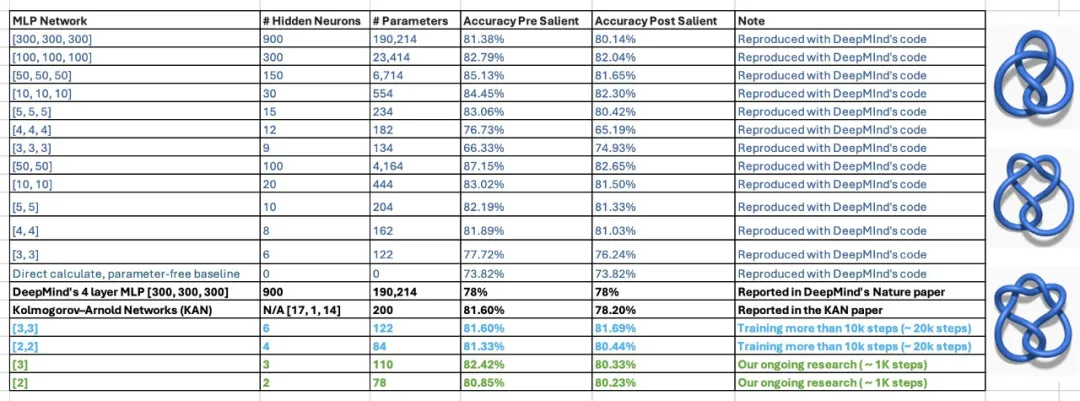
對(duì)此，論文作者也給出了積極的回應(yīng)：  

第二，KAN 和 MLP 從方法上沒(méi)有本質(zhì)不同。

「是的，這顯然是一回事。他們?cè)?KAN 中先做激活，然后再做線性組合，而在 MLP 中先做線性組合，然后再做激活。將其放大，基本上就是一回事。據(jù)我所知，使用 KAN 的主要原因是可解釋性和符號(hào)回歸。」

除了對(duì)方法的質(zhì)疑之外，研究者還呼吁對(duì)這篇論文的評(píng)價(jià)回歸理性：

「我認(rèn)為人們需要停止將 KAN 論文視為深度學(xué)習(xí)基本單元的巨大轉(zhuǎn)變，而只是將其視為一篇關(guān)于深度學(xué)習(xí)可解釋性的好論文。在每條邊上學(xué)習(xí)到的非線性函數(shù)的可解釋性是這篇論文的主要貢獻(xiàn)。」

第三，有研究者表示，KAN 的思路并不新奇。

「人們?cè)?20 世紀(jì) 80 年代對(duì)此進(jìn)行了研究。Hacker News 的討論中提到了一篇意大利論文討論過(guò)這個(gè)問(wèn)題。所以這根本不是什么新鮮事。40 年過(guò)去了，這只是一些要么回來(lái)了，要么被拒絕的東西被重新審視的東西。」

但可以看到的是，KAN 論文的作者也沒(méi)有掩蓋這一問(wèn)題。

「這些想法并不新鮮，但我不認(rèn)為作者回避了這一點(diǎn)。他只是把所有東西都很好地打包起來(lái)，并對(duì) toy 數(shù)據(jù)進(jìn)行了一些很好的實(shí)驗(yàn)。但這也是一種貢獻(xiàn)。」

與此同時(shí)，Ian Goodfellow、Yoshua Bengio 十多年前的論文 MaxOut（https://arxiv.org/pdf/1302.4389）也被提到，一些研究者認(rèn)為二者「雖然略有不同，但想法有點(diǎn)相似」。

作者：最初研究目標(biāo)確實(shí)是可解釋性

熱烈討論的結(jié)果就是，作者之一 Sachin Vaidya 站出來(lái)了。

作為該論文的作者之一，我想說(shuō)幾句。KAN 受到的關(guān)注令人驚嘆，而這種討論正是將新技術(shù)推向極限、找出哪些可行或不可行所需要的。

我想我應(yīng)該分享一些關(guān)于動(dòng)機(jī)的背景資料。我們實(shí)現(xiàn) KAN 的主要想法源于我們正在尋找可解釋的人工智能模型，這種模型可以「學(xué)習(xí)」物理學(xué)家發(fā)現(xiàn)自然規(guī)律的洞察力。因此，正如其他人所意識(shí)到的那樣，我們完全專注于這一目標(biāo)，因?yàn)閭鹘y(tǒng)的黑箱模型無(wú)法提供對(duì)科學(xué)基礎(chǔ)發(fā)現(xiàn)至關(guān)重要的見(jiàn)解。然后，我們通過(guò)與物理學(xué)和數(shù)學(xué)相關(guān)的例子表明，KAN 在可解釋性方面大大優(yōu)于傳統(tǒng)方法。我們當(dāng)然希望，KAN 的實(shí)用性將遠(yuǎn)遠(yuǎn)超出我們最初的動(dòng)機(jī)。

在 GitHub 主頁(yè)中，論文作者之一劉子鳴也對(duì)這項(xiàng)研究受到的評(píng)價(jià)進(jìn)行了回應(yīng)：

最近我被問(wèn)到的最常見(jiàn)的問(wèn)題是 KAN 是否會(huì)成為下一代 LLM。我對(duì)此沒(méi)有很清楚的判斷。

KAN 專為關(guān)心高精度和可解釋性的應(yīng)用程序而設(shè)計(jì)。我們確實(shí)關(guān)心 LLM 的可解釋性，但可解釋性對(duì)于 LLM 和科學(xué)來(lái)說(shuō)可能意味著截然不同的事情。我們關(guān)心 LLM 的高精度嗎？縮放定律似乎意味著如此，但可能精度不太高。此外，對(duì)于 LLM 和科學(xué)來(lái)說(shuō)，準(zhǔn)確性也可能意味著不同的事情。

我歡迎人們批評(píng) KAN，實(shí)踐是檢驗(yàn)真理的唯一標(biāo)準(zhǔn)。很多事情我們事先并不知道，直到它們經(jīng)過(guò)真正的嘗試并被證明是成功還是失敗。盡管我愿意看到 KAN 的成功，但我同樣對(duì) KAN 的失敗感到好奇。

KAN 和 MLP 不能相互替代，它們?cè)谀承┣闆r下各有優(yōu)勢(shì)，在某些情況下各有局限性。我會(huì)對(duì)包含兩者的理論框架感興趣，甚至可以提出新的替代方案（物理學(xué)家喜歡統(tǒng)一理論，抱歉）。

KAN 論文一作劉子鳴。他是一名物理學(xué)家和機(jī)器學(xué)習(xí)研究員，目前是麻省理工學(xué)院和 IAIFI 的三年級(jí)博士生，導(dǎo)師是 Max Tegmark。他的研究興趣主要集中在人工智能 AI 和物理的交叉領(lǐng)域。