反轉了?在一場新較量中,號稱替代MLP的KAN只贏一局
多層感知器 (Multi-Layer Perceptrons,MLP) ,也被稱為全連接前饋神經網絡,是當今深度學習模型的基本組成部分。MLP 的重要性無論怎樣強調都不為過,因為它是機器學習中用于逼近非線性函數的默認方法。
然而,MLP 也存在某些局限性,例如難以解釋學習到的表示,以及難以靈活地擴展網絡規模。
KAN(Kolmogorov–Arnold Networks)的出現,為傳統 MLP 提供了一種創新的替代方案。該方法在準確性和可解釋性方面優于 MLP,而且,它能以非常少的參數量勝過以更大參數量運行的 MLP。
那么,問題來了,KAN 、MLP 到底該選哪一種?有人支持 MLP,因為 KAN 只是一個普通的 MLP,根本替代不了,但也有人則認為 KAN 更勝一籌,而當前對兩者的比較也是局限在不同參數或 FLOP 下進行的,實驗結果并不公平。
為了探究 KAN 的潛力,有必要在公平的設置下全面比較 KAN 和 MLP 了。
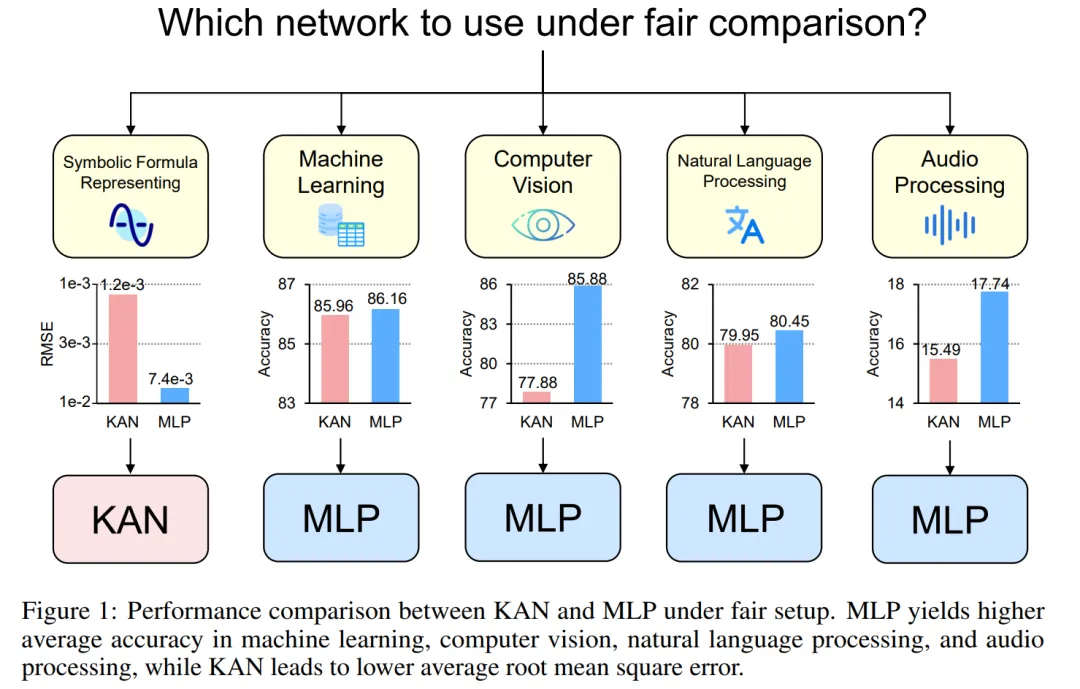
為此,來自新加坡國立大學的研究者在控制了 KAN 和 MLP 的參數或 FLOP 的情況下,在不同領域的任務中對它們進行訓練和評估,包括符號公式表示、機器學習、計算機視覺、NLP 和音頻處理。在這些公平的設置下,他們發現 KAN 僅在符號公式表示任務中優于 MLP,而 MLP 通常在其他任務中優于 KAN。

- 論文地址:https://arxiv.org/pdf/2407.16674
- 項目鏈接:https://github.com/yu-rp/KANbeFair
- 論文標題:KAN or MLP: A Fairer Comparison
作者進一步發現,KAN 在符號公式表示方面的優勢源于其使用的 B - 樣條激活函數。最初,MLP 的整體性能落后于 KAN,但在用 B - 樣條代替 MLP 的激活函數后,其性能達到甚至超過了 KAN。但是,B - 樣條無法進一步提高 MLP 在其他任務(如計算機視覺)上的性能。
作者還發現,KAN 在連續學習任務中的表現實際上并不比 MLP 好。最初的 KAN 論文使用一系列一維函數比較了 KAN 和 MLP 在連續學習任務中的表現,其中每個后續函數都是前一個函數沿數軸的平移。而本文比較了 KAN 和 MLP 在更標準的類遞增持續學習設置中的表現。在固定的訓練迭代條件下,他們發現 KAN 的遺忘問題比 MLP 更嚴重。
KAN、MLP 簡單介紹
KAN 有兩個分支,第一個分支是 B 樣條分支,另一個分支是 shortcut 分支,即非線性激活與線性變換連接在一起。在官方實現中,shortcut 分支是一個 SiLU 函數,后面跟著一個線性變換。令 x 表示一個樣本的特征向量。那么,KAN 樣條分支的前向方程可以寫成:
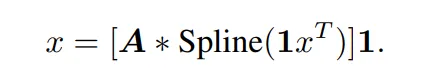
在原始 KAN 架構中,樣條函數被選擇為 B 樣條函數。每個 B 樣條函數的參數與其他網絡參數一起學習。
相應的,單層 MLP 的前向方程可以表示為:
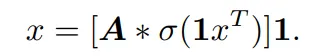
該公式與 KAN 中的 B 樣條分支公式具有相同的形式,只是在非線性函數中有所不同。因此,拋開原論文對 KAN 結構的解讀,KAN 也可以看作是一種全連接層。
因而,KAN 和普通 MLP 的區別主要有兩點:
- 激活函數不同。通常 MLP 中的激活函數包括 ReLU、GELU 等,沒有可學習的參數,對所有輸入元素都是統一的,而在 KAN 中,激活函數是樣條函數,有可學習的參數,并且對于每個輸入元素都是不一樣的。
- 線性和非線性運算的順序。一般來說,研究者會把 MLP 概念化為先進行線性變換,再進行非線性變換,而 KAN 其實是先進行非線性變換,再進行線性變換。但在某種程度上,將 MLP 中的全連接層描述為先非線性,后線性也是可行的。
通過比較 KAN 和 MLP,該研究認為兩者之間的差異主要是激活函數。因而,他們假設激活函數的差異使得 KAN 和 MLP 適用于不同的任務,從而導致兩個模型在功能上存在差異。為了驗證這一假設,研究者比較了 KAN 和 MLP 在不同任務上的表現,并描述了每個模型適合的任務。為了確保公平比較,該研究首先推導出了計算 KAN 和 MLP 參數數量和 FLOP 的公式。實驗過程控制相同數量的參數或 FLOP 來比較 KAN 和 MLP 的性能。
KAN 和 MLP 的參數數量及FLOP
控制參數數量
KAN 中可學習的參數包括 B 樣條控制點、shortcut 權重、B 樣條權重和偏置項。總的可學習參數數量為:
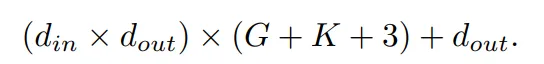
其中, d_in 和 d_out 表示神經網絡層的輸入和輸出維度,K 表示樣條的階數,它與官方 nn.Module KANLayer 的參數 k 相對應,它是樣條函數中多項式基礎的階數。G 表示樣條間隔數,它對應于官方 nn.Module KANLayer 的 num 參數。它是填充前 B 樣條曲線的間隔數。在填充之前,它等于控制點的數量 - 1。在填充后,應該有 (K +G) 個有效控制點。
相應的,一個 MLP 層的可學習參數是:
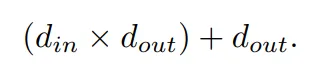
KAN 和 MLP 的 FLOP
在作者的評估中,任何算術操作的 FLOP 被考慮為 1,而布爾操作的 FLOP 被考慮為 0。De Boor-Cox 算法中的 0 階操作可以轉換為一系列布爾操作,這些操作不需要進行浮點運算。因此,從理論上講,其 FLOP 為 0。這與官方 KAN 實現不同,在官方實現中,它將布爾數據轉換回浮點數據來進行操作。
在作者的評估中,FLOP 是針對一個樣本計算的。官方 KAN 代碼中使用 De Boor-Cox 迭代公式實現的 B 樣條 FLOP 為:
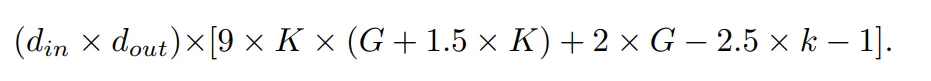
連同 shortcut 路徑的 FLOP 以及合并兩個分支的 FLOP,一個 KAN 層的總 FLOP 是:
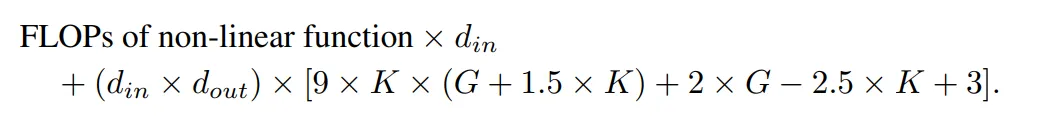
相應的,一個 MLP 層的 FLOP 為:

具有相同輸入維度和輸出維度的 KAN 層與 MLP 層之間的 FLOP 差異可以表示為:
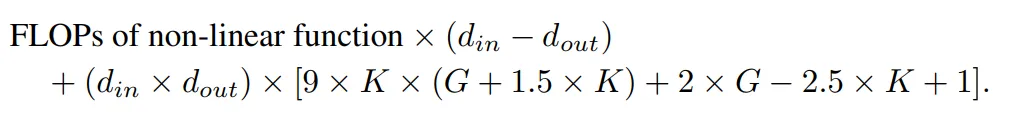
如果 MLP 也首先進行非線性操作,那么首項將為零。
實驗
作者的目標是,在參數數量或 FLOP 相等的前提下,對比 KAN 和 MLP 的性能差異。該實驗涵蓋多個領域,包括機器學習、計算機視覺、自然語言處理、音頻處理以及符號公式表示。所有實驗都采用了 Adam 優化器,這些實驗全部在一塊 RTX3090 GPU 上進行。
性能比較
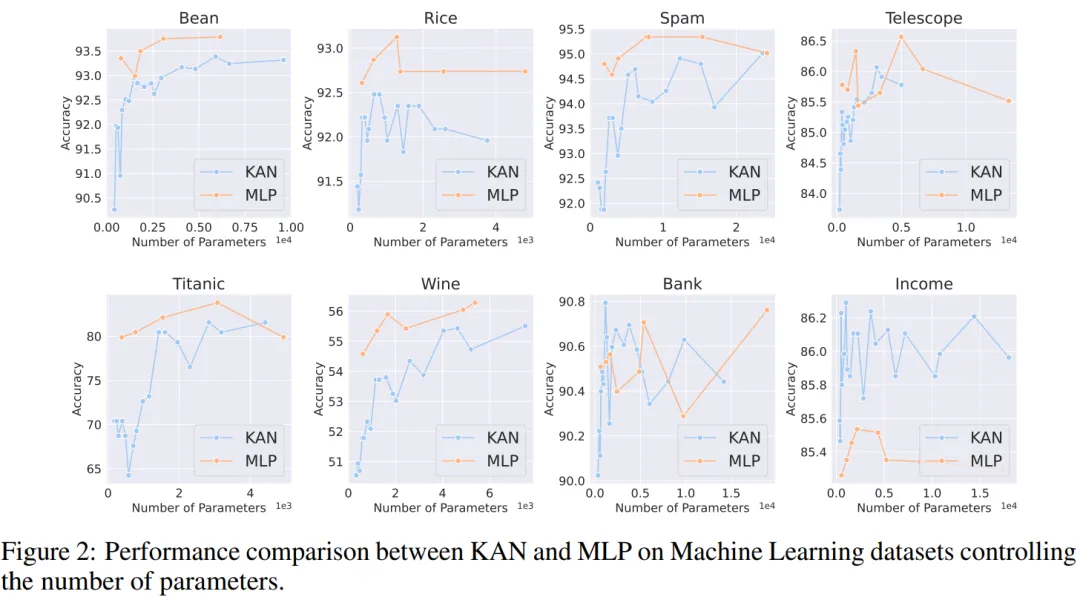
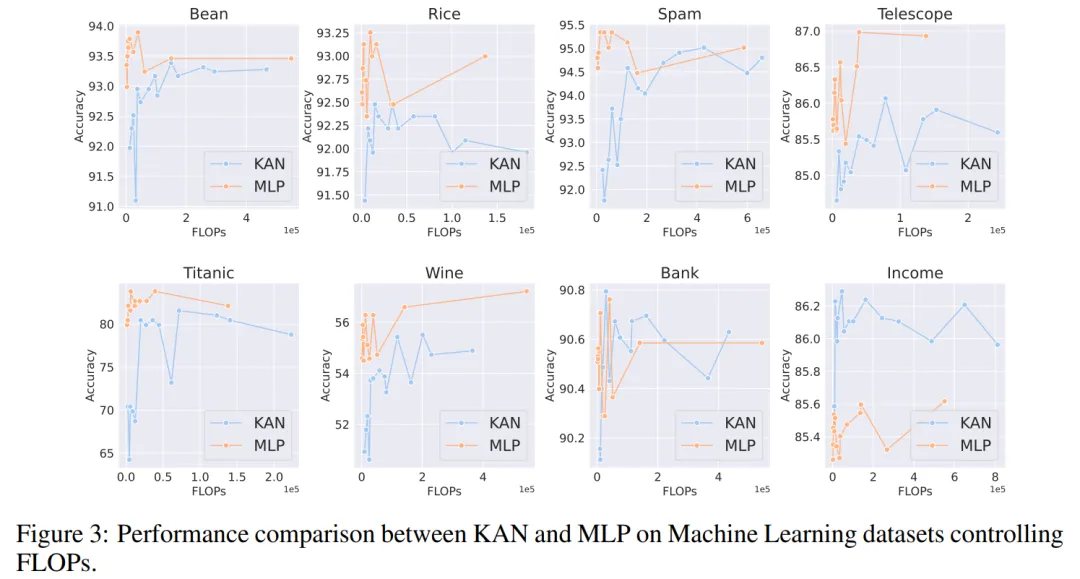
機器學習。作者在 8 個機器學習數據集上進行了實驗,使用了具有一到兩個隱藏層的 KAN 和 MLP,根據各個數據集的特點,他們調整了神經網絡的輸入和輸出維度。
對于 MLP,隱藏層寬度設置為 32、64、128、256、512 或 1024,并采用 GELU 或 ReLU 作為激活函數,同時在 MLP 中使用了歸一化層。對于 KAN,隱藏層寬度則為 2、4、8 或 16,B 樣條網格數為 3、5、10 或 20,B 樣條的度數(degree)為 2、3 或 5。
由于原始 KAN 架構不包括歸一化層,為了平衡 MLP 中歸一化層可能帶來的優勢,作者擴大了 KAN 樣條函數的取值范圍。所有實驗都進行了 20 輪訓練,實驗記錄了訓練過程中在測試集上取得的最佳準確率,如圖 2 和圖 3 所示。
在機器學習數據集上,MLP 通常保持優勢。在他們對八個數據集的實驗中,MLP 在其中的六個上表現優于 KAN。然而,他們也觀察到在一個數據集上,MLP 和 KAN 的性能幾乎相當,而在另一個數據集上,KAN 表現則優于 MLP。
總體而言,MLP 在機器學習數據集上仍然具有普遍優勢。
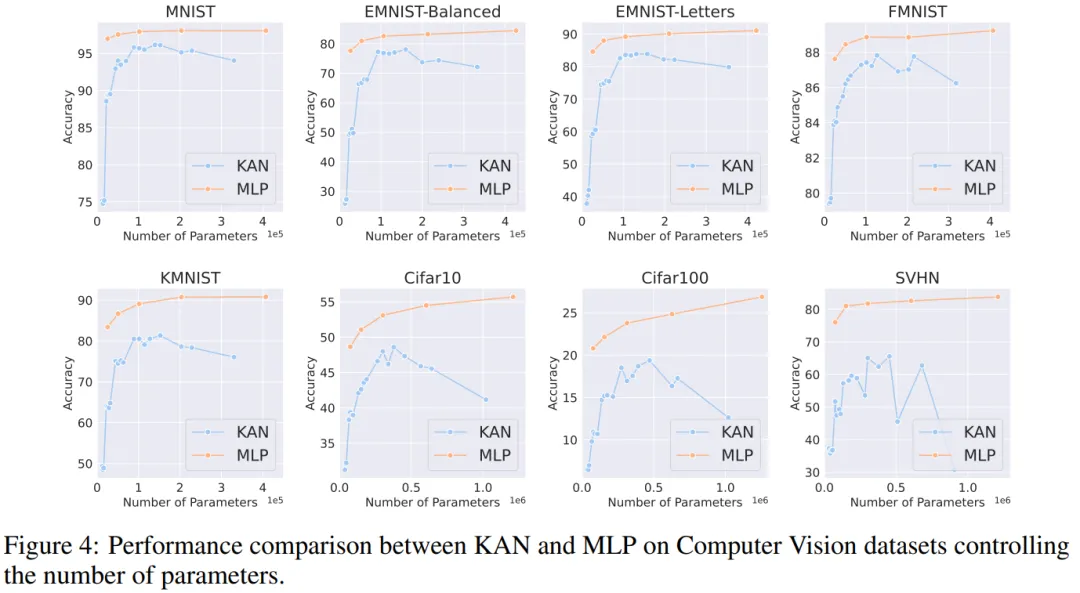
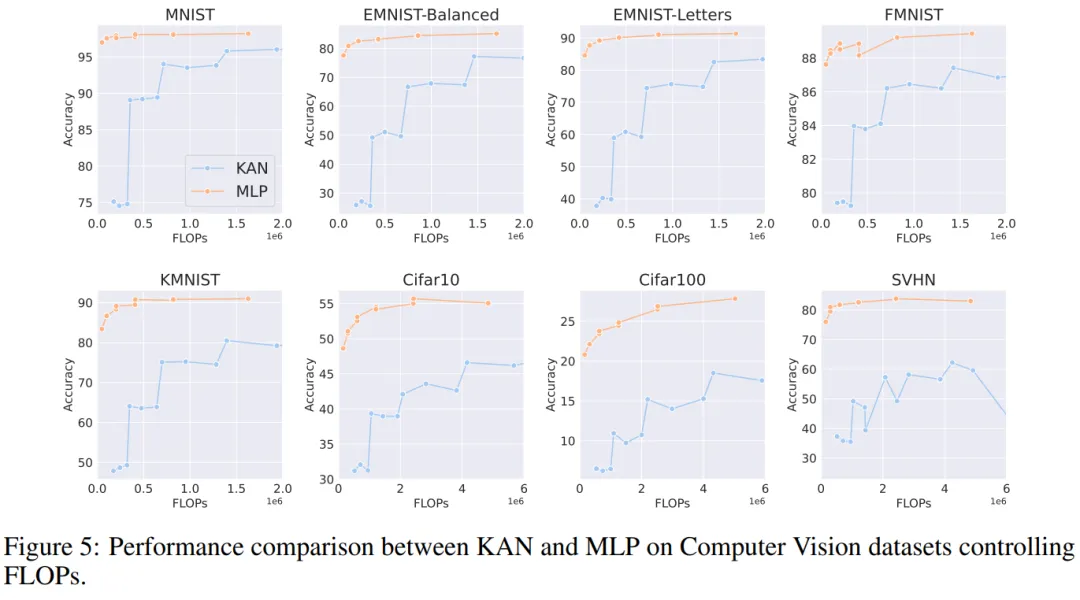
計算機視覺。作者對 8 個計算機視覺數據集進行了實驗。他們使用了具有一到兩個隱藏層的 KAN 和 MLP,根據數據集的不同,調整了神經網絡的輸入和輸出維度。
在計算機視覺數據集中,KAN 的樣條函數引入的處理偏差并沒有起到效果,其性能始終不如具有相同參數數量或 FLOP 的 MLP。
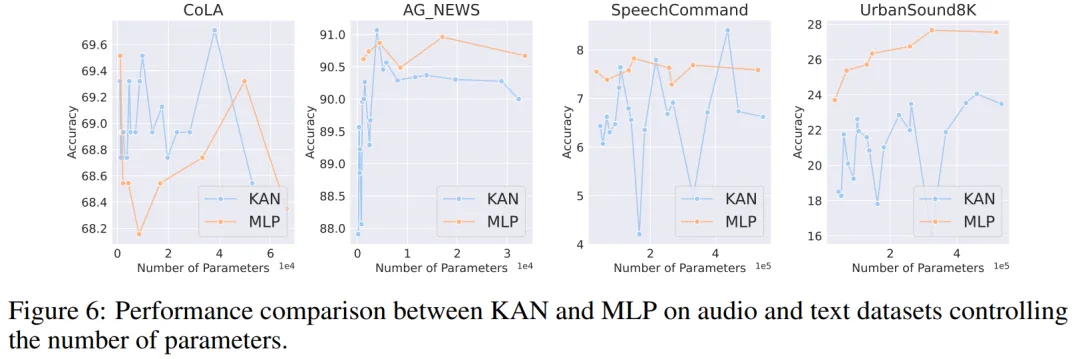
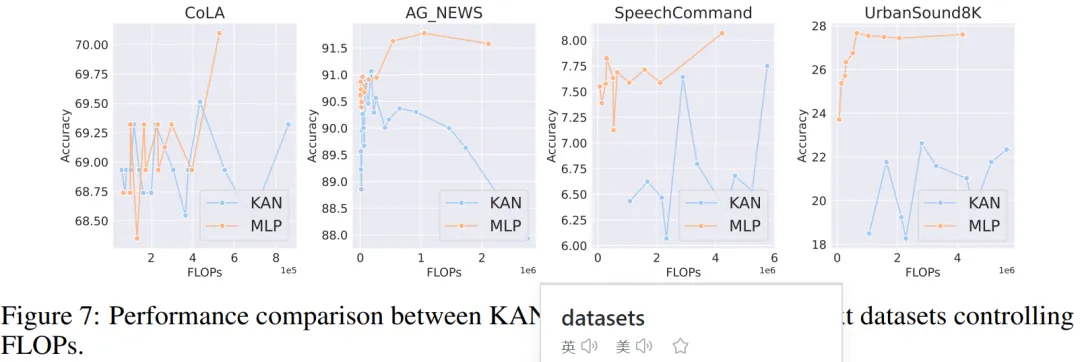
音頻和自然語言處理。作者在 2 個音頻分類和 2 個文本分類數據集上進行了實驗。他們使用了一到兩個隱藏層的 KAN 和 MLP,并根據數據集的特性,調整了神經網絡的輸入和輸出維度。
在兩個音頻數據集上,MLP 的表現優于 KAN。
在文本分類任務中,MLP 在 AG 新聞數據集上保持了優勢。然而,在 CoLA 數據集上,MLP 和 KAN 之間的性能沒有顯著差異。當控制參數數量相同時,KAN 在 CoLA 數據集上似乎有優勢。然而,由于 KAN 的樣條函數需要較高的 FLOP,這一優勢在控制 FLOP 的實驗中并未持續顯現。當控制 FLOP 時,MLP 似乎更勝一籌。因此,在 CoLA 數據集上,并沒有一個明確的答案來說明哪種模型更好。
總體而言,MLP 在音頻和文本任務中仍然是更好的選擇。
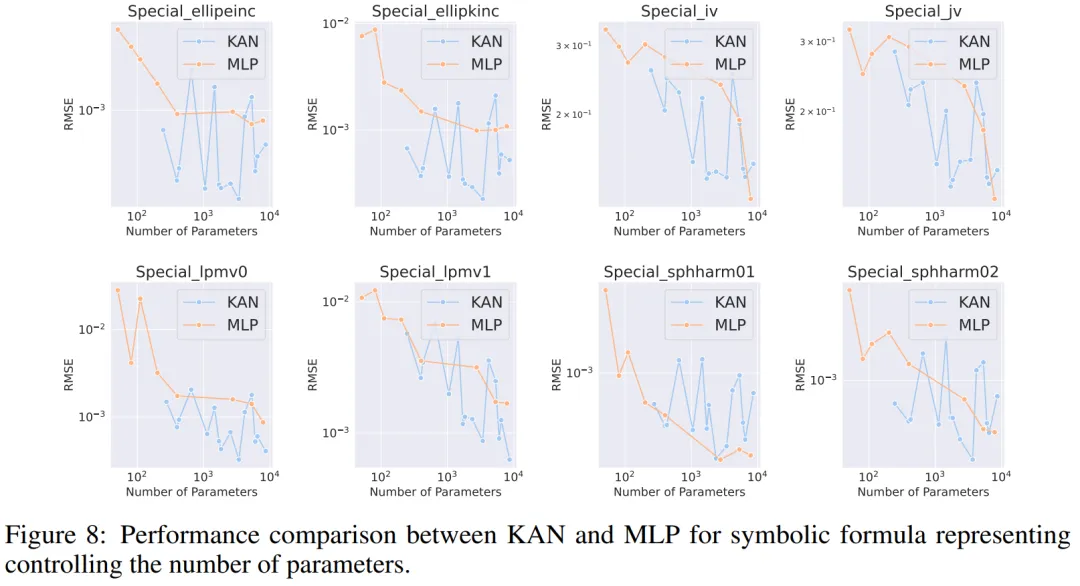
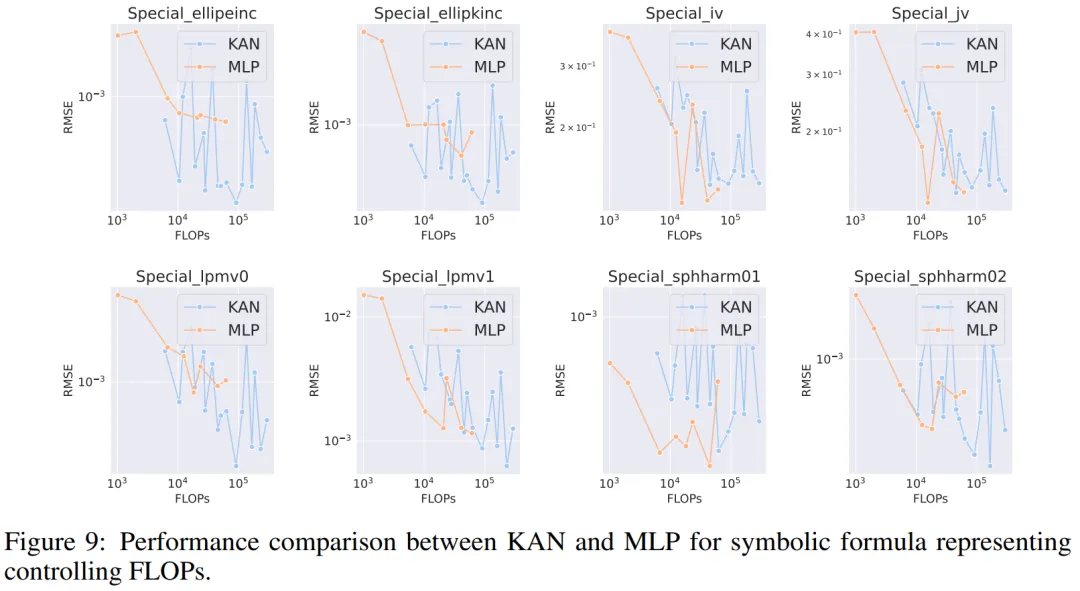
符號公式表示。作者在 8 個符號公式表示任務中比較了 KAN 和 MLP 的差異。他們使用了一到四個隱藏層的 KAN 和 MLP,根據數據集調整了神經網絡的輸入和輸出維度。
在控制參數數量的情況下,KAN 在 8 個數據集中的 7 個上表現優于 MLP。在控制 FLOP 時,由于樣條函數引入了額外的計算復雜性,KAN 的性能大致與 MLP 相當,在兩個數據集上優于 MLP,在另一個數據集上表現不如 MLP。
總體而言,在符號公式表示任務中,KAN 的表現優于 MLP。