分位數回歸滿足這一需求，提供具有量化機會的預測區間。它是一種統計技術，用于模擬預測變量與響應變量之間的關系，特別是當響應變量的條件分布令人感興趣時。與傳統的回歸方法不同，分位數回歸側重于估計響應變量的條件量值，而不是條件均值。

圖(A): 分位數回歸

分位數回歸概念 

分位數回歸是估計?組回歸變量X與被解釋變量Y的分位數之間線性關系的建模?法。

以往的回歸模型實際上是研究被解釋變量的條件期望。??們也關?解釋變量與被解釋變量分布的 中位數，分位數呈何種關系。它最早由Koenker和Bassett(1978)提出。

OLS回歸估計量的計算是基于最?化殘差平?。分位數回歸估計量的計算也是基于?種?對稱形式 的絕對值殘差最?化。其中，中位數回歸運?的是最?絕對值離差估計(LAD，least absolute deviations estimator)。 

分位數回歸的優點 

（1）能夠更加全?的描述被解釋變量條件分布的全貌，?不是僅僅分析被解釋變量的條件期望（均 值），也可以分析解釋變量如何影響被解釋變量的中位數、分位數等。不同分位數下的回歸系數估 計量常常不同，即解釋變量對不同?平被解釋變量的影響不同。  

（2）中位數回歸的估計?法與最??乘法相?，估計結果對離群值則表現的更加穩健，?且，分位 數回歸對誤差項并不要求很強的假設條件，因此對于?正態分布??，分位數回歸系數估計量則更 加穩健。

分位數回歸相對于蒙特卡羅模擬具有哪些優勢呢？首先，分位數回歸直接估計給定預測因子的響應變量的條件量值。這意味著，它不像蒙特卡羅模擬那樣產生大量可能的結果，而是提供了響應變量分布的特定量級的估計值。這對于了解不同層次的預測不確定性特別有用，例如二分位數、四分位數或極端量值。其次，分位數回歸提供了一種基于模型的預測不確定性估算方法，利用觀測數據來估計變量之間的關系，并根據這種關系進行預測。相比之下，蒙特卡羅模擬依賴于為輸入變量指定概率分布，并根據隨機抽樣生成結果。

NeuralProphet提供兩種統計技術：(1) 分位數回歸和 (2)保形分位數回歸。共形分位數預測技術增加了一個校準過程來做分位數回歸。在本章中，我們將使用 Neural Prophet 的分位數回歸模塊。

環境要求

安裝 NeuralProphet。

!pip install neuralprophet
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

導入需要的庫。

%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")

數據集

共享單車數據。該數據集是一個多變量數據集，包含每日租賃需求以及溫度或風速等其他天氣領域。

data = pd.read_csv('/bike_sharing_daily.csv')
data.tail()

圖(B): 共享單車

繪制共享單車的數量圖。我們觀察到，需求量在第二年有所增加，而且有季節性規律。

# convert string to datetime64
data["ds"] = pd.to_datetime(data["dteday"])

# create line plot of sales data
plt.plot(data['ds'], data["cnt"])
plt.xlabel("date")
plt.ylabel("Count")
plt.show()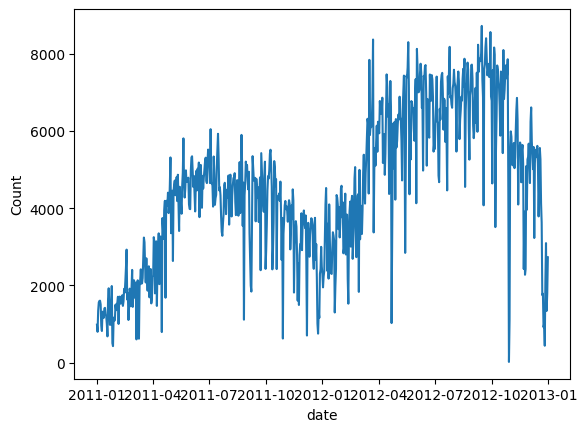

圖 (C)：自行車租賃日需求量

為建模做最基本的數據準備。NeuralProphet 要求列名為 ds 和 y，這與 Prophet 的要求相同。

df = data[['ds','cnt']]
df.columns = ['ds','y']

構建分位數回歸模型

直接在 NeuralProphet 中構建分位數回歸。假設我們需要第 5、10、50、90 和 95 個量級的值。我們指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打開參數 quantiles = quantile_list。

from neuralprophet import NeuralProphet, set_log_level

quantile_list=[0.05,0.1,0.5,0.9,0.95 ]
# Model and prediction
m = NeuralProphet(
    quantiles=quantile_list,
    yearly_seasnotallow=True,
    weekly_seasnotallow=True,
    daily_seasnotallow=False
)
m = m.add_country_holidays("US")
m.set_plotting_backend("matplotlib")  # Use matplotlib

df_train, df_test = m.split_df(df, valid_p=0.2)
metrics = m.fit(df_train, validation_df=df_test, progress="bar")
metrics.tail()

分位數回歸預測

我們將使用 .make_future_dataframe()為預測創建新數據幀，NeuralProphet 是基于 Prophet 的。參數 n_historic_predictions 為 100，只包含過去的 100 個數據點。如果設置為 True，則包括整個歷史數據。我們設置 period=50 來預測未來 50 個數據點。

future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)

# Perform prediction with the trained models
forecast = m.predict(df=future)
forecast.tail(60)

預測結果存儲在數據框架 predict 中。

圖 (D)：預測

上述數據框架包含了繪制地圖所需的所有數據元素。

m.plot(
    forecast, 
    plotting_backend="plotly-static"
    #plotting_backend = "matplotlib"
)

預測區間是由分位數值提供的！

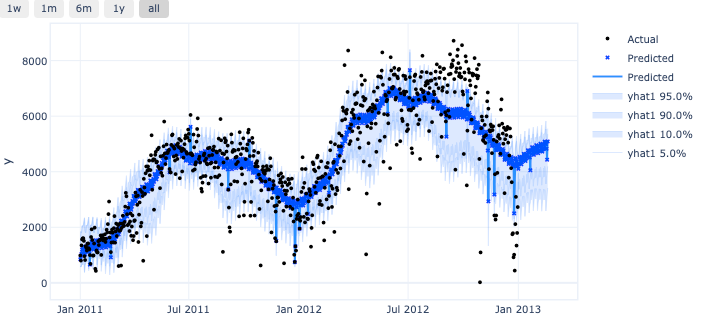圖 (E)：分位數預測

預測區間和置信區間的區別

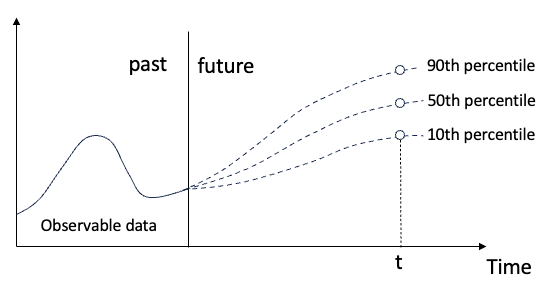
預測區間和置信區間在流行趨勢中很有幫助，因為它們可以量化不確定性。它們的目標、計算方法和應用是不同的。下面我將用回歸來解釋兩者的區別。在圖(F)中，我在左邊畫出了線性回歸，在右邊畫出了分位數回歸。

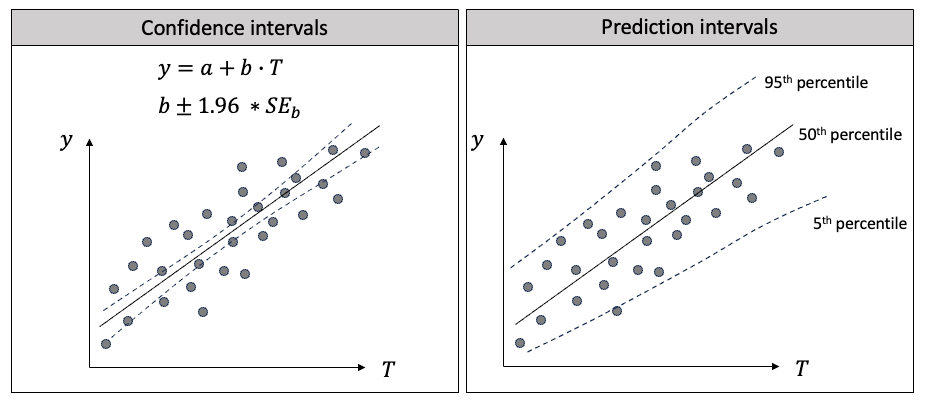圖(F)：置信區間與預測區間的區別

首先，它們的目標不同：

• 線性回歸的主要目標是找到一條線，使預測值盡可能接近給定自變量值時因變量的條件均值。
• 分位數回歸旨在提供未來觀測值的范圍，在一定的置信度下。它估計自變量與因變量條件分布的不同量化值之間的關系。

其次，它們的計算方法不同：

• 在線性回歸中，置信區間是對自變量系數的區間估計，通常使用普通最小二乘法 (OLS) 找出數據點到直線的最小總距離。系數的變化會影響預測的條件均值 Y。
• 在分位數回歸中，你可以選擇依賴變量的不同量級來估計回歸系數，通常是最小化絕對偏差的加權和，而不是使用OLS方法。

第三，它們的應用不同：

• 在線性回歸中，預測的條件均值有 95% 的置信區間。置信區間較窄，因為它是條件平均值，而不是整個范圍。
• 在分位數回歸中，預測值有 95% 的概率落在預測區間的范圍內。

寫在最后

本文介紹了分位數回歸預測區間的概念，以及如何利用 NeuralProphet 生成預測區間。我們還強調了預測區間和置信區間之間的差異，這在商業應用中經常引起混淆。后面將繼續探討另一項重要的技術，即復合分位數回歸（CQR），用于預測不確定性。