深入探索堆:Go語言中的高效數據結構
堆,作為一種基本的數據結構,以其在優先隊列和排序算法中提供高效解決方案的能力而聞名。在本文中,我們將深入探討堆的內部工作原理,包括其特性、實現細節以及在現代編程中的應用。
堆基礎
堆是一種特殊的二叉樹,其中每個父節點都根據特定標準與子節點保持一定的關系。在最大堆中,父節點的值總是大于或等于其子節點的值;在最小堆中,情況則相反。這種結構的主要優勢在于能夠快速訪問和提取最高或最低優先級的元素。
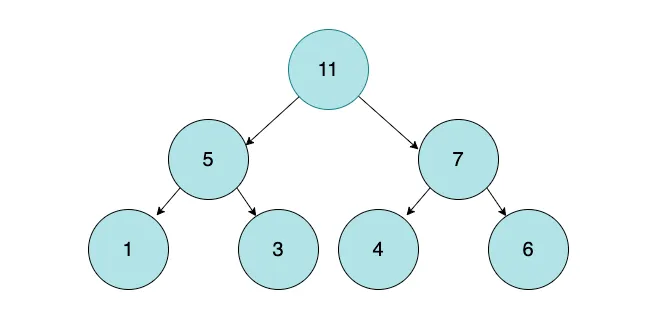 圖片
圖片
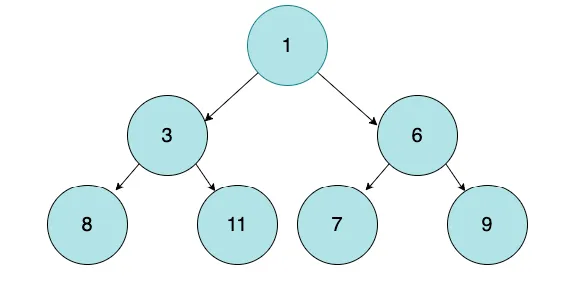 圖片
圖片
堆操作
推操作(Push)
- 將新元素添加到樹的末尾。
- 將其與父節點進行比較。
- 如有必要,與父節點交換位置,以維護堆屬性。
- 重復此過程,直到元素到達根節點或滿足堆屬性。
彈出操作(Pop)
- 將根節點與樹的最后一個元素交換。
- 刪除最后一個元素(即原根節點)。
- 對新的根節點執行“向下堆化”操作,確保堆屬性得以維持。
實現細節
堆通常使用數組實現,這種實現方式利用了內存的連續性和直接索引的特性,從而實現高效的元素訪問和操作。
時間復雜度
- 推操作(Push): O(logN)
- 彈出操作(Pop): O(logN)
- N 代表堆中元素的數量。
索引計算
- 父節點索引:(當前索引 - 1)/ 2
- 左子節點索引:當前索引 * 2 + 1
- 右子節點索引:當前索引 * 2 + 2
Go語言中的實現
在Go中,我們可以選擇直接實現堆,或者使用標準庫中的container/heap包。以下是兩種方法的示例:
直接實現
// MaxHeap 是一個最大堆的實現
type MaxHeap struct {
array []int
}
// Insert 向最大堆中插入一個新元素
func (h *MaxHeap) Insert(key int) {
h.array = append(h.array, key)
h.heapifyUp(len(h.array) - 1)
}
// ExtractMax 從最大堆中提取并返回最大元素
func (h *MaxHeap) ExtractMax() (int, error) {
if h.IsEmpty() {
return 0, errors.New("heap is empty")
}
// ... 提取和堆化代碼 ...
}
// IsEmpty 檢查堆是否為空
func (h *MaxHeap) IsEmpty() bool {
return len(h.array) == 0
}
// Size 返回堆的大小
func (h *MaxHeap) Size() int {
return len(h.array)
}
// ... heapifyUp 和 heapifyDown 方法 ...使用 container/heap
// MaxHeap 使用 Go 的堆接口實現最大堆
type MaxHeap []int
// Len 返回堆的長度
func (h MaxHeap) Len() int { return len(h) }
// Less 定義堆中元素的比較標準
func (h MaxHeap) Less(i, j int) bool { return h[i] > h[j] }
// Swap 交換堆中的元素
func (h MaxHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
// Push 向堆中添加一個元素
func (h *MaxHeap) Push(x interface{}) {
*h = append(*h, x.(int))
}
// Pop 從堆中移除并返回頂部元素
func (h *MaxHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
// ... 堆操作示例 ...實際應用
堆的實用性廣泛,它在以下領域中發揮著重要作用:
- 優先隊列:動態地對任務或事件進行優先級排序。
- 堆排序:一種高效的數組排序算法,時間復雜度為 O(nlogn)。
- 網絡路由:根據數據包的優先級,優化計算機網絡中的路由決策。
- 內存管理:支持編程語言和操作系統中的動態內存分配與回收。
結語
堆不僅是數據結構領域的基石,更是現代編程中高效管理優先級數據的關鍵工具。它的分層組織和對數時間復雜度使其在算法設計和系統優化中扮演著不可或缺的角色。掌握堆的原理和操作,將為工程師和開發人員提供解決復雜問題、構建高效系統的強大工具集。






































