排序是一種組織數(shù)據(jù)的方式，目的是確保數(shù)據(jù)元素之間的相對順序正確。當我們提到比較排序，意味著我們通過兩兩比較來確定元素之間的順序。

理論上，一個最優(yōu)的比較排序算法應(yīng)該在每次比較后盡量減少剩余的可能性。

為了理解這點，考慮一個 N 個元素的所有 N! 種排列方式。在最優(yōu)的方法中，每次比較都能使剩下的可能性減半，從 N!/2，N!/4，N!/8，...，N!/（2^k），……，1。

所以，對于 N 個元素的序列，為了確定一個特定的排列，最下限的情況下，我們需要進行 log(N!) 次比較。這是因為當 2^k = N! 時，k = log(N!)。

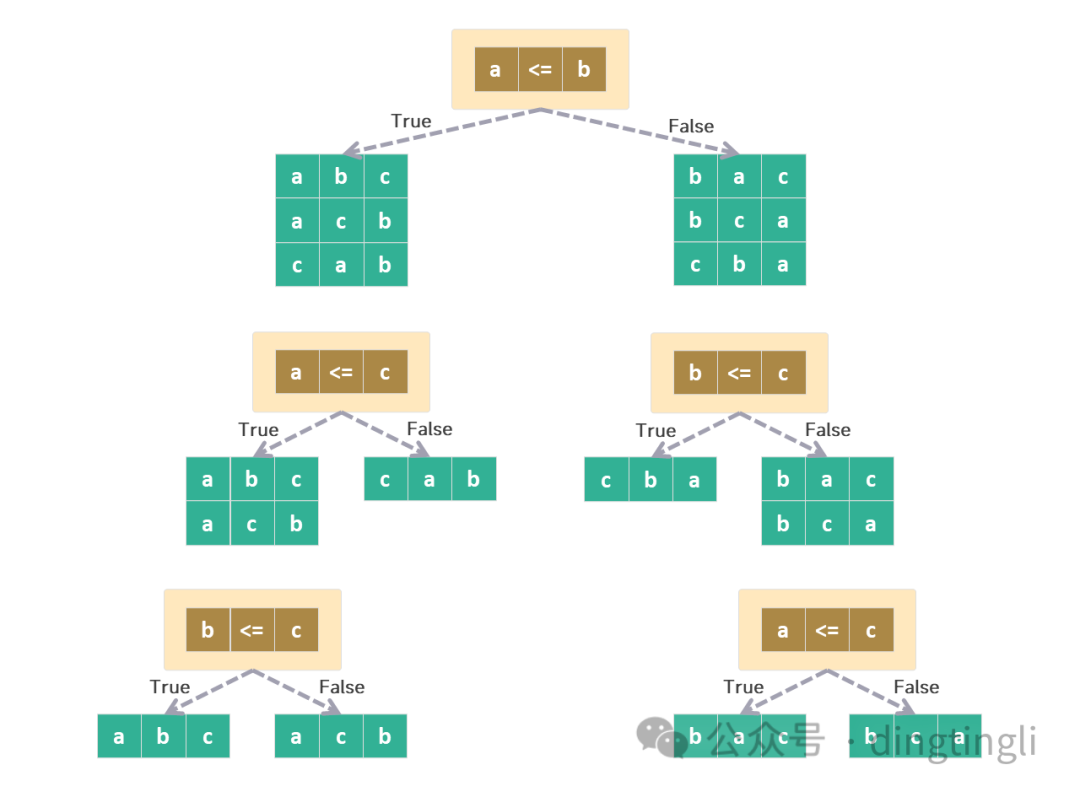
三個元素 a，b，c 序列的排序

但為什么現(xiàn)有的排序算法還不能達到這種理想狀態(tài)呢？

為什么堆排序（HEAPSORT）不夠快

首先，讓我們回顧一下堆排序的實現(xiàn)：

1. 建立最大堆： 將任意數(shù)組轉(zhuǎn)化為最大堆。
2. 找到最大元素并交換： 最大的元素始終位于數(shù)組的第一個位置，將數(shù)組的第一個元素與最后一個元素交換。
3. 重建最大堆： 排除最后一個元素，并在剩余的元素中重新構(gòu)建最大堆。
4. 重復(fù)上述過程： 繼續(xù)交換、排除和重建。

詳情可以閱讀之前的文章：堆排序的原理與實現(xiàn)。

問題出在第二步，根據(jù)最大堆的定義，底部元素較小。堆排序?qū)⑤^小的元素從堆的底部提升到頂部，然后再讓它們逐漸下沉，與較大的元素交換位置。

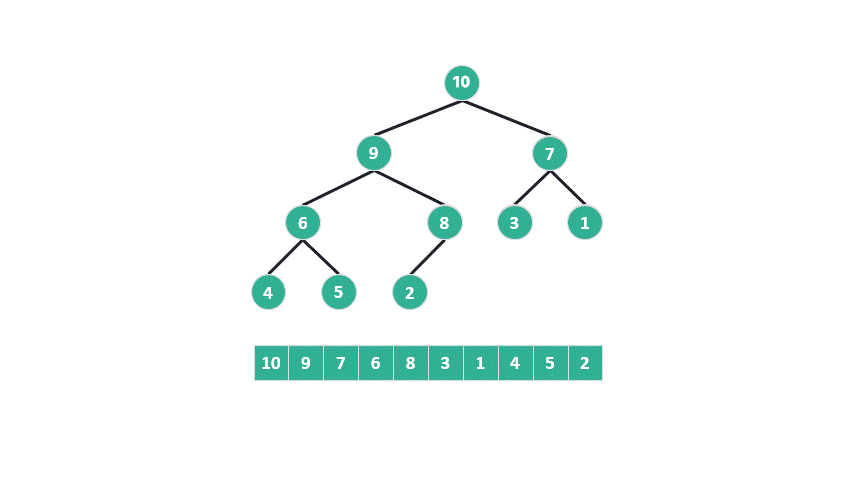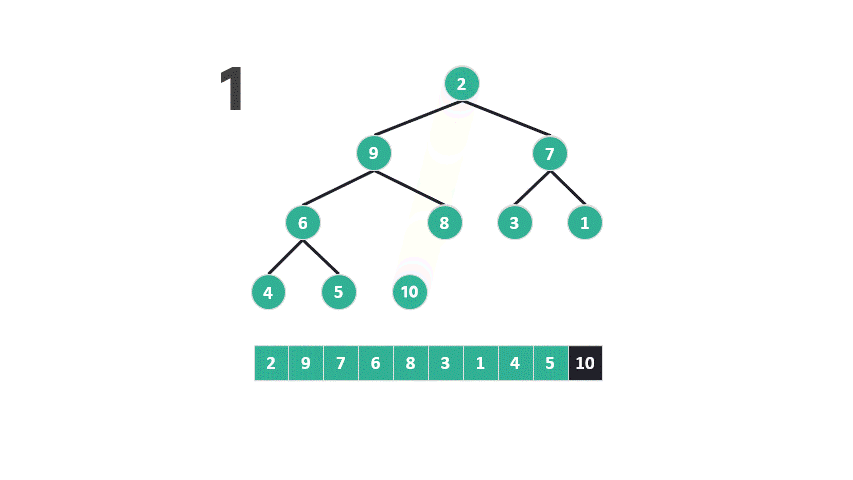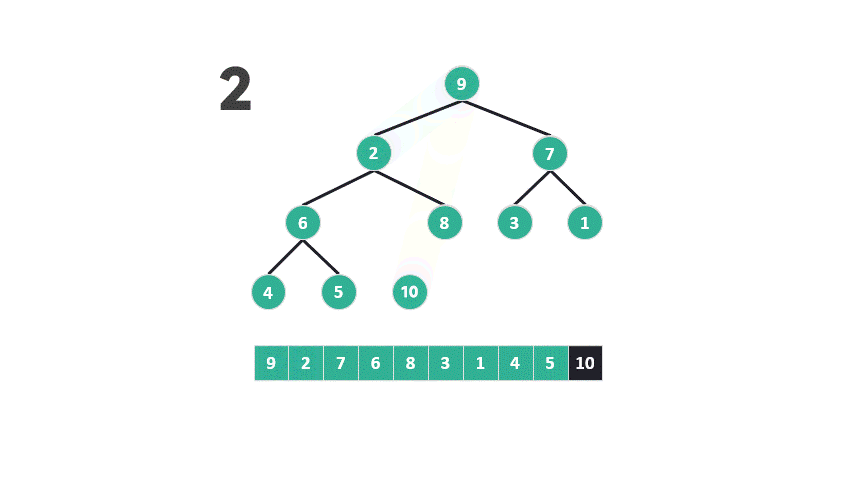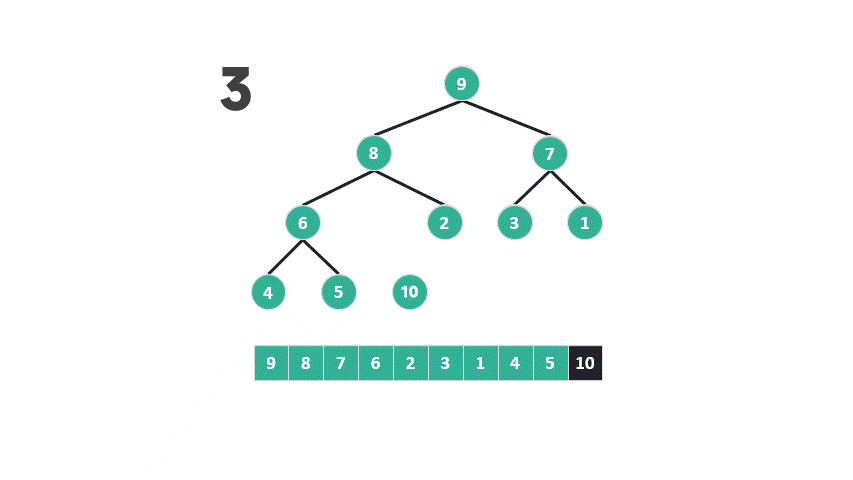動圖 重建最大堆示意圖

你可以在我的 github 倉庫中查看堆排序源代碼：

https://github.com/dingtingli/algorithm/blob/main/Code/heapsort01.py

這種操作在堆排序中似乎違反了直覺：為什么要將底部可能較小的元素提升到更高的位置，然后觀察其下沉的過程？

當?shù)撞吭乇惶嵘秊楦腹?jié)點時，它幾乎總是小于其中一個子節(jié)點，而大于另一個子節(jié)點的機會相對較少。因此，重建最大堆時進行的比較具有不均等的概率。這種概率不均等的比較是低效的，因為它不能保證每次比較都能將可能性減半。

這種操作效率的問題是堆排序速度較慢的主要原因。

然而，我們可以嘗試以下優(yōu)化方法：

優(yōu)化方法的思想，就好比一個公司的老板離職需要被組織中最優(yōu)秀的人替代，我們顯然需要比較兩位副總裁；問題是，我們是否期望這將是一場勢均力敵的競爭？

在沒有先驗信息的情況下，我們沒有充分的理由押注任何一位副總裁。情況中只有一種不對稱性：這兩個部門的總?cè)藬?shù)可能不等。副總裁"A"可能是比"副總裁"B"稍多的人中的佼佼者；一個大部門的最優(yōu)秀者更有可能擊敗一個小部門的最優(yōu)秀者。

優(yōu)化后的 HEAPSORT：

1. 將所有元素放入有效的最大堆中
2. 刪除堆頂，創(chuàng)建一個空缺 "V"
3. 比較 V 正下方的兩個子堆首領(lǐng)，將最大的那個提升到空缺中。
4. 遞歸重復(fù)第 3 步，重新定義 V 為新的空缺，直到堆的底部。
5. 轉(zhuǎn)到步驟 2

你可以在我的 github 倉庫中查看快速堆排序源代碼：

https://github.com/dingtingli/algorithm/blob/main/Code/heapsort03.py

這種方法的優(yōu)勢在于，我們實際上是將一個已知較大的元素提升至堆頂，無需額外的比較操作。此時，兩種比較結(jié)果的概率是均等的。我們將這種優(yōu)化版本稱為 "快速堆排序"（FAST HEAPSORT）。

經(jīng)過優(yōu)化后的 "快速堆排序"很有可能是最接近理論極限的排序算法。

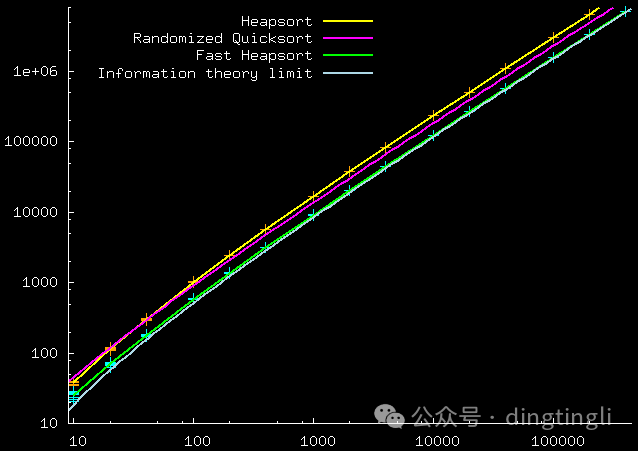快速堆排序

橫坐標：要排序的項目數(shù) N。縱坐標：二分比較次數(shù)。

理論曲線顯示了快速堆排序的漸近結(jié)果（2NlnN）和極限 log_2 N! 近似。

為什么快速排序（QUICKSORT）不夠快

快速排序的核心分為兩個過程：

1. 選擇數(shù)組中的一個元素為支點（pivot），將小于等于支點的元素移到左側(cè)，將大于支點的元素移動到右側(cè)。這一步稱為劃分（partition）。
2. 通過遞歸對左右兩側(cè)的子數(shù)組繼續(xù)劃分，直到數(shù)組排序完成。

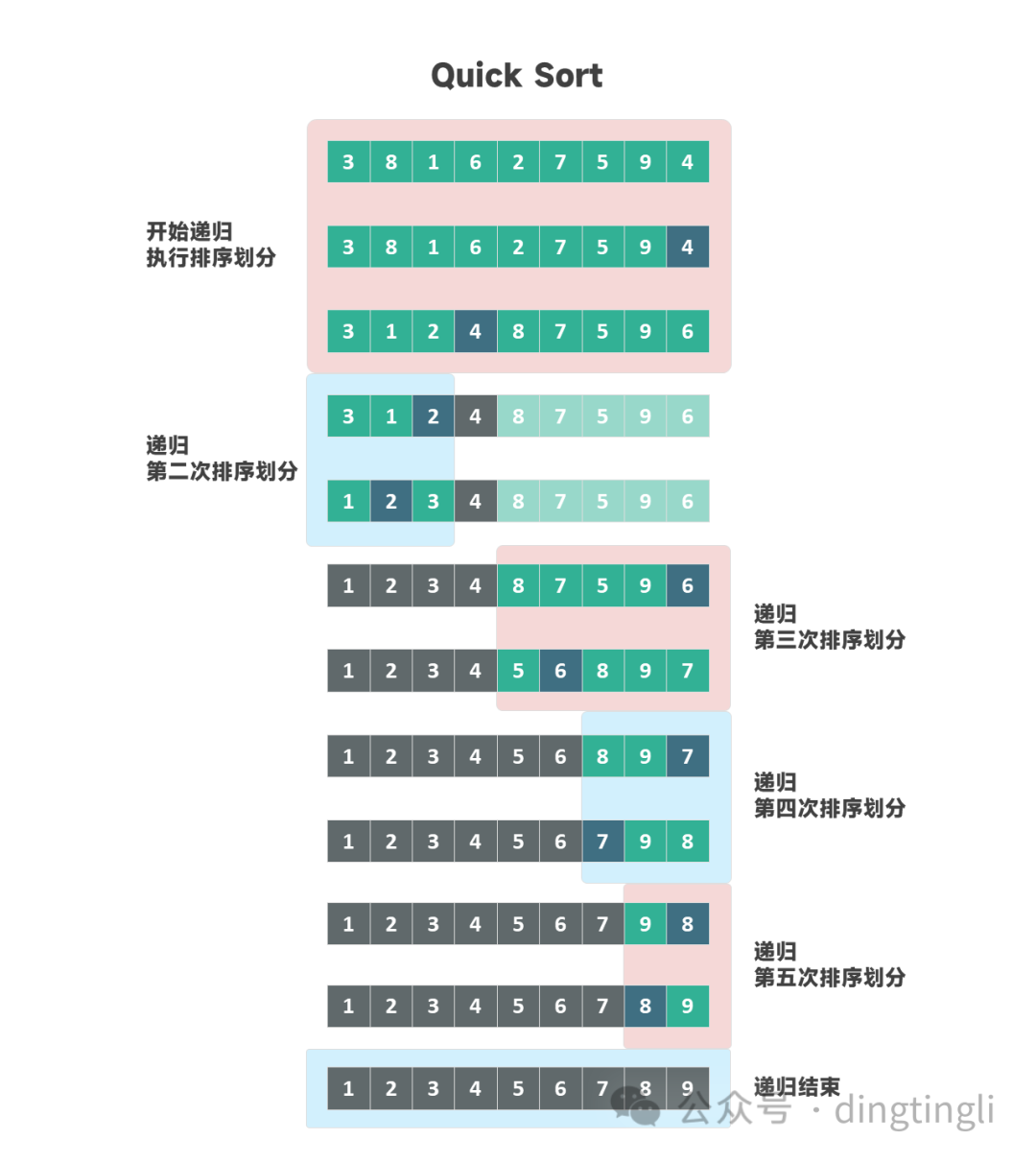劃分遞歸執(zhí)行

詳情可以閱讀之前的文章：快速排序的原理與實現(xiàn)。

為了進一步說明，假設(shè)有一個由三個元素組成的序列：pivot, a1 和 a2。

在快速排序的劃分階段，首先，我們會將 a1 與 pivot 進行比較。顯然，(a1 < pivot) 和 (a1 > pivot) 可能性各占一半，這使得第一次比較達到了理想的效果。

然而，第二次的比較并不像第一次那樣完美。

假設(shè)第一次比較已經(jīng)確定 (a1 < pivot) ，此時我們需要進一步判斷 a2 與 pivot 之間的關(guān)系。

考慮所有的組合可能性：基于 a1、a2 和 pivot 的相對順序，總共存在 3! 即 6 種可能的排列：

1. (a1 < a2 < pivot)
2. (a1 < pivot < a2)
3. (a2 < a1 < pivot)
4. (a2 < pivot < a1)
5. (pivot < a1 < a2)
6. (pivot < a2 < a1)

由于已知 (a1 < pivot)，第 4、第 5 和第 6 種情況可以直接排除，這使得我們只考慮：

1. (a1 < a2 < pivot)
2. (a1 < pivot < a2)
3. (a2 < a1 < pivot)

在這三種情況中，(a2 < pivot) 的可能性有 2 種，而 (a2 > pivot) 的情況僅有 1 種。

所以 (a2 < pivot) 的概率是 2/3，而 (a2 > pivot) 的概率是 1/3。

這就是快排也不那么快的原因，因為它并不總能確保每次比較都將可能性減半。

為什么基數(shù)排序（RADIXSORT）很快

基數(shù)排序之所以高效，是因為它脫離了傳統(tǒng)比較排序的框架，不再通過兩兩元素的比較來決定排序順序。

想象一下這樣一個任務(wù)：整理一副撲克牌中同一花色的牌。假設(shè)手中有 N（N≤13）張牌，要如何迅速地給它們排好序呢？可以想象桌上已經(jīng)預(yù)留出了 13 個特定的位置，每張牌會根據(jù)其點數(shù)被精準地放在對應(yīng)位置。

比如，2 點的牌會放在第二個位置，而 Q 則被放置在第 12 個位置。所有牌放好后，按照位置順序收集，你就得到了有序的撲克牌。

這個例子揭示了基數(shù)排序的核心效率。每張新牌的放置位置實際上是在前 i 張牌所定義的 i+1 個區(qū)間中選擇的。

例如，如果我們已經(jīng)放置了 2,5,8 這三張牌，那么我們就有四個區(qū)間來放置下一張牌：2 之前、2 和 5 之間、 5 和 8 之間，以及 8 之后。

當你放置第 i+1 張牌時，你實際上是在這些 i+1 個區(qū)間中選擇一個位置放置它。一旦選擇了一個區(qū)間放置新牌，其他的 i 個區(qū)間都被排除了。

因此，每放置一張新牌，你都減少了大約 i/i+1 的排序可能性。而基于比較的排序方法，每次操作最多只能減少排序可能性的一半。

比較排序的本質(zhì)就像我們之前介紹的二分法游戲，然而除了二分法，我們還介紹了三分法游戲。基數(shù)排序更進一步，本質(zhì)就像是 N 分法。

看圖聊算法：一個游戲讓你理解二分法的本質(zhì)

看圖聊算法：還是一個游戲，讓你理解三分法的本質(zhì)

這就是基數(shù)排序之所以高效的原因，它擺脫了比較的排序算法復(fù)雜度上限只能是 O(NlogN) 的命運。

然而，基數(shù)排序有其局限性。比如需要知道數(shù)據(jù)的范圍或?qū)挾龋抑饕m用于整數(shù)和字符串。對于浮點數(shù)和復(fù)數(shù)，基數(shù)排序也不太合適。

結(jié)論

在算法中，我們通常使用大O記號來描述復(fù)雜度。但這種表示并非完美無缺。當我們使用"O"符號強調(diào)“對于大N的漸進性能”，這似乎暗示我們對 O(4NlogN) 和 O(1NlogN) 兩種算法之間的差異不甚關(guān)心。

然而，這種常數(shù)因子的差異仍然是眾多研究者追求和努力的焦點。即使排序算法的時間復(fù)雜度已達到理論上的界限 O(NlogN)，其演進仍在繼續(xù)。

參考資料：

[1] http://www.inference.org.uk/mackay/sorting/sorting.html

[2] http://mindhacks.cn/2008/06/13/why-is-quicksort-so-quick