聊一聊算法之旅:棧
本質棧是一種特殊的數據結構,它特殊在它的結構,與數組、鏈表不同的是,它的數據出入規則是:先進后出,后進先出。
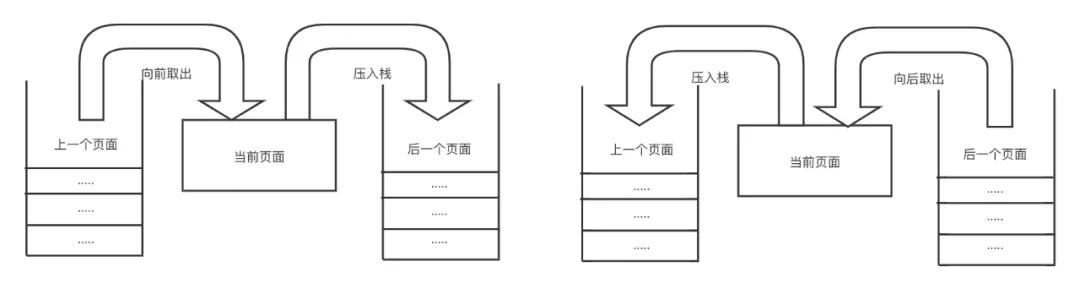
由于它這種特殊的特性,它一般用于指定的場景之下,例如:瀏覽器的前進與回退效果。
瀏覽器的特性是:我們可以向前訪問我們之前訪問的網站,也可以向后訪問后面的網站。
瀏覽器的這種特性,完美匹配了棧的結構。
我們只需使用兩個棧,分別代表瀏覽器的向前訪問與向后訪問。
當某個數據集合只涉及在一端插入和刪除數據,并且滿足先進后出,后進先出的特性,這時我們應該首先想到的是棧,看它是否能夠更好的實現我們所需的場景。
實現方式棧的實現方式有兩種,一種是基于數組的實現方式,稱為順序棧;另一種是基于鏈表的實現方式,稱為鏈式棧。
這兩種實現方式區別不是很多,實現之后棧的出入時間復雜度都是O(1)。
不同的是基于數組實現的棧消耗的內存更少,因為它不需要額外保存指向的指針。
但基于數組的另外一額外需要做的是,如果需要實現不定大小的棧,它需要實現動態擴容,這是所有基于數組實現的一個必修課。
下面我們來實現一個基于數組的順序棧,為了減少復雜度,不考慮擴容的情況。
// 基于數組實現的順序棧class ArrayStack(private val n: Int) { private val items = arrayOfNulls
基于上面的實現,我們能夠很容易得出棧的出入時間復雜度為O(1)。
另一方面,由于沒有額外的空間申請,所以棧的空間復雜度為O(1)。
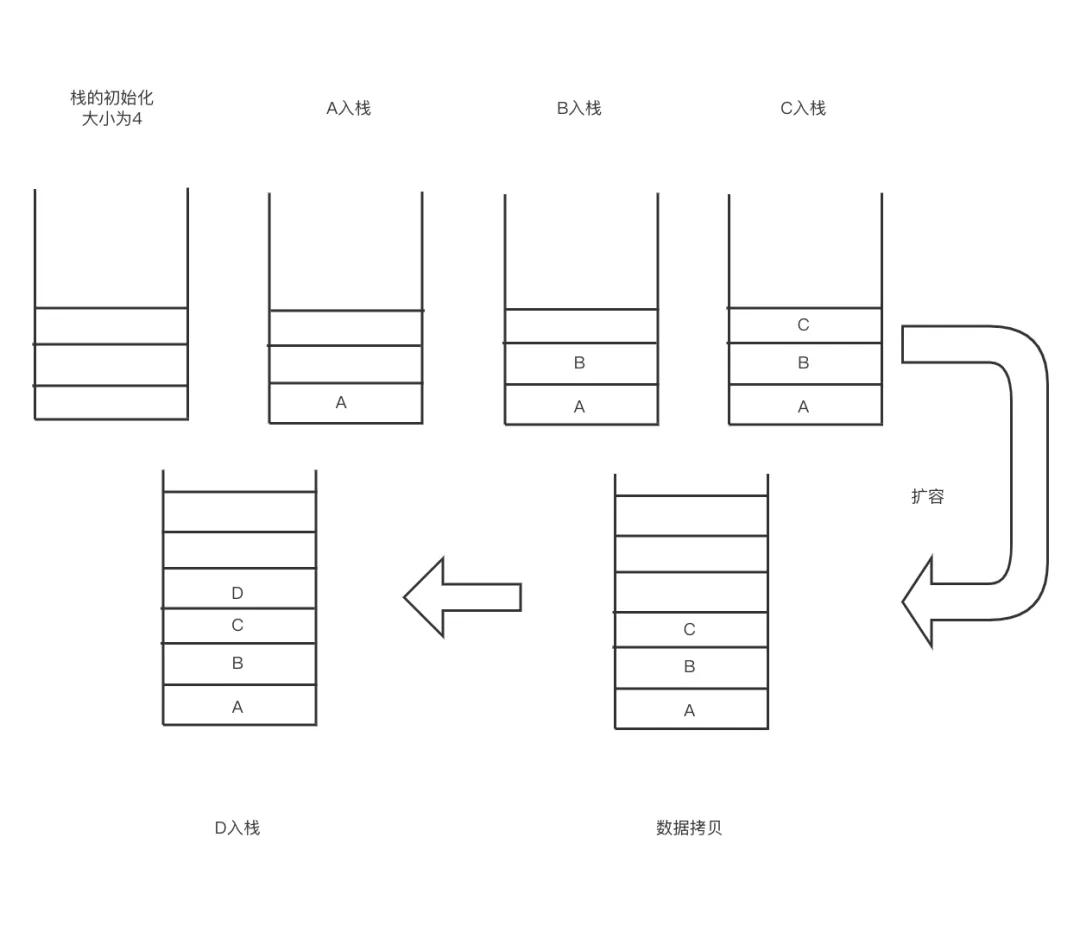
擴容上面我們實現的是一個固定的順序棧,也就是說初始化的時候已經指定了棧的大小,當棧滿了的時候,無法進行向棧中添加數據。當然基于鏈表的鏈式棧沒有這種限制。
為了解決順序棧的這種限制,我們需要對數據進行擴容操作,這在數組那一節也有提及過。
所以,如果要實現一個支持擴容的棧,我們只需底層依賴一個基于擴容的數組即可。
具體的擴容示意圖如下:
具體代碼實現可以查看數據的擴容。
下面我們再來分析一下基于數組擴容的棧的時間復雜度。
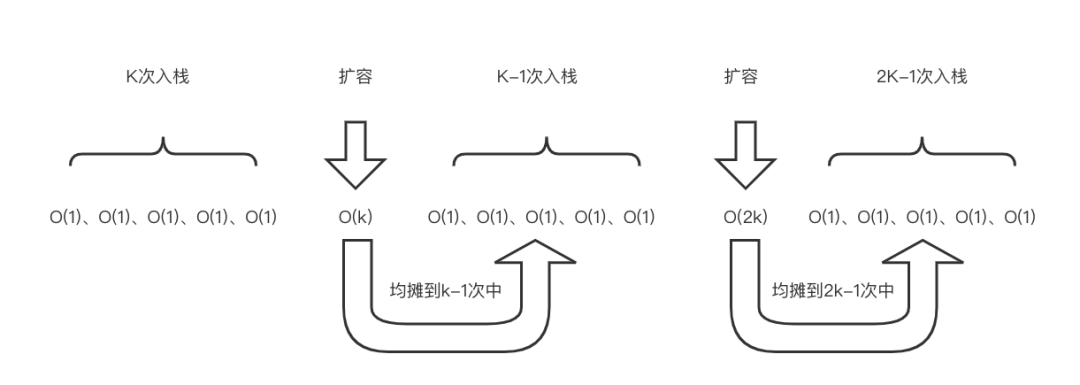
首先未達到棧的大小時,這一階段與固定的順序棧一樣,出入的時間復雜度都為O(1)。
當數據為K時且達到擴容的臨界點時,需要將數組的大小擴大到原來的兩倍,并將之前的數據拷貝的新的數組中;這一階段消耗的時間復雜度為O(K)。
當擴容結束之后繼續出入棧,此時的時間復雜度又為O(1)。
當再一次達到2k時又需要再次擴容,拷貝數據到新數組中,此時消耗的時間復雜度為O(2k)。
反復重復以上步驟。
這就是支持擴容的順序棧的時間復雜度的變化。也就是說最好情況的時間復雜度為O(1);最壞的時間復雜度為O(n)。那么平均時間復雜度呢?
還記得在算法之旅:復雜度分析中提到的均攤時間復雜度嗎?
下面我們就利用均攤時間復雜度來分析它的平均時間復雜度。其實看一張圖就能夠明白均攤時間復雜度的算法。
每次我們都將擴容的所消耗的時間都分攤到之后的入棧中。在分攤之前入棧需要一個push的時間;分攤之后入棧在push的時間上再加上一個數據move的時間。push與move的時間復雜度都為O(1)。
所以均攤之后棧的整個時間復雜度就是O(1),即棧的平均復雜度為O(1)。
棧的應用現在我們已經對棧有了一個全面的了解,為了完全鞏固棧這種數據結構,我們剩下的就是練習以達到熟悉程度。
例如:實現一個基本的計算器來計算一個簡單的字符串表達式的值, 字符串表達式可以包含左括號(,右括號),加號+,減號-,非負整數和空格。
基于表達式的運算,非常符合棧這種結構,我們可以使用棧來實現的。實現思路如下:
通過設定一個符號位將所有的運算轉化成加法
遇到數字都帶上之前的符號位,再與之前的結果做加法運算
遇到'('將之前的符號位與結果保留到棧中,然后再重復1 2步驟計算括號里面的值
遇到')'取出之前保留的符號位與結果,與當前結果做加法運算
/** * O(n) */fun calculate(s: String): Int { val numberStack = Stack
還有一些關于棧的經典練習,如果能夠掌握這些,那么有關棧的算法就基本沒什么問題了
比較含退格的字符串
棒球比賽
下一個更大元素
有效的括號
我將源碼放在Github上了,如有需要的可以自行查看。
本文轉載自微信公眾號「 Android補給站」,可以通過以下二維碼關注。轉載本文請聯系 Android補給站公眾號。