在本系列的 上一篇文章中，我們學習了使用 Anaconda，加強了概率論的知識。在本文中我們將繼續學習概率論的知識，學習使用 seaborn 和 Pandas 進行數據可視化，并進一步介紹 TensorFlow 和 Keras 的使用。

讓我們從增長人工智能和機器學習的理論知識開始。眾所周知人工智能、機器學習、數據科學、深度學習等是當今計算機科學的熱門話題。然而，計算機科學還其他熱門的話題，比如 區塊鏈blockchain、物聯網Internet of Things（IoT）、量子計算quantum computing等。那么，人工智能領域的發展是否會對這些技術產生積極的影響呢？

首先，讓我們討論一下區塊鏈。根據維基百科的定義，“區塊鏈是一種分布式賬本，它由不斷增長的記錄（稱為 區塊block）組成，這些記錄使用加密技術安全地連接在一起。”乍一看，人工智能和區塊鏈似乎是兩個高速發展的獨立技術。但令人驚訝的是，事實并非如此。區塊鏈相關的行話是 完整性integrity，人工智能相關的行話是數據。我們將大量數據交給人工智能程序去處理。雖然這些應用程序產生了驚人的結果，但我們如何信任它們呢？這就提出了對可解釋的人工智能的需求。它可以提供一定的保證，以便最終用戶可以信任人工智能程序提供的結果。許多專家認為，區塊鏈技術可以用來提高人工智能軟件做出的決策的可信度。另一方面，智能合約smart contract（區塊鏈技術的一部分）可以從人工智能的驗證中受益。從本質上講，智能合約和人工智能通常都是做決策。因此，人工智能的進步將對區塊鏈技術產生積極影響，反之亦然。

下面讓我們討論一下人工智能和物聯網之間的影響。早期的物聯網設備通常沒有強大的處理能力或備用電池。這使得需要大量處理能力的機器學習的軟件無法部署在物聯網設備上。當時，大多數物聯網設備中只部署了基于規則的人工智能軟件。基于規則的人工智能的優勢在于它很簡單，需要相對較少的處理能力。如今的物聯網設備具備更強大的處理能力，可以運行更強大的機器學習軟件。特斯拉開發的高級駕駛輔助系統 特斯拉自動駕駛儀Tesla Autopilo

最后，讓我們討論人工智能和量子計算是如何相互影響的。盡管量子計算仍處于起步階段，但 量子機器學習quantum machine learning（QML）是其中非常重要的課題。量子機器學習基于兩個概念：量子數據和量子-經典混合模型。量子數據是由量子計算機產生的數據。量子神經網絡quantum neural network（QNN）用于模擬量子計算模型。TensorFlow Quantum 是一個用于量子-經典混合機器學習的強大工具。這類工具的存在表明，在不久的將來將會有越來越多的基于量子計算的人工智能解決方案。

seaborn 入門

seaborn 是一個基于 Matplotlib 的數據可視化 Python 庫。用它能夠繪制美觀且信息豐富的統計圖形。通過 Anaconda Navigator 可以輕松安裝 seaborn。我用 ESPNcricinfo 網站上 T20 國際板球賽的擊球記錄，創建了一個名為 T20.csv 的 CSV（逗號分隔值comma-separated value）文件，其中包含以下 15 列：球員姓名、職業生涯跨度、比賽場次、局數、未出局次數、總得分、最高得分、平均得分、面對球數、擊球率、百分次數、五十分次數、零分次數、四分次數和六分次數。圖 1 是使用 Pandas 庫讀取這個 CSV 文件的程序代碼。我們已經在前面介紹過 Pandas 了。

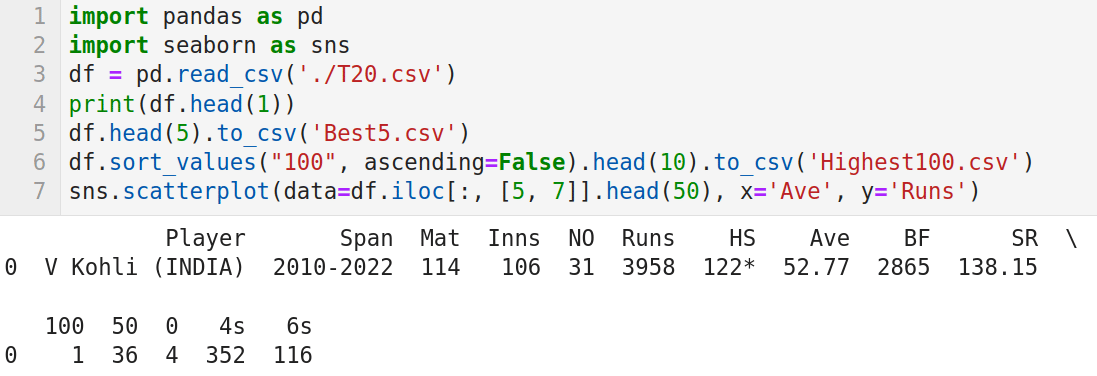圖 1：使用 seaborn 的簡單例子

下面逐行解釋程序代碼的作用。第 1 行和第 2 行導入 Pandas 和 seaborn 包。第 3 行從 JupyterLab 的工作目錄中讀取文件 T20.csv。第 4 行打印元數據和第一行數據。圖 1 顯示了這行數據，它顯示了 T20 國際板球賽中得分最高的 Virat Kohli 的擊球記錄。第 5 行將元數據和 T20.csv 中的前五行數據保存到 Best5.csv 中。在執行該行代碼時會在 JupyterLab 的工作目錄中創建這個文件。第 6 行根據列百分次數按升序對 CSV 文件進行排序，并將前 10 名世紀得分手的詳細信息存儲到 Highest100.csv 中。該文件也將存儲在 JupyterLab 的工作目錄中。最后，第7行代碼提取了第 5 列（總得分）和第 7 列（平均得分）的數據信息，并生成散點圖。圖 2 顯示了程序在執行時生成的散點圖。

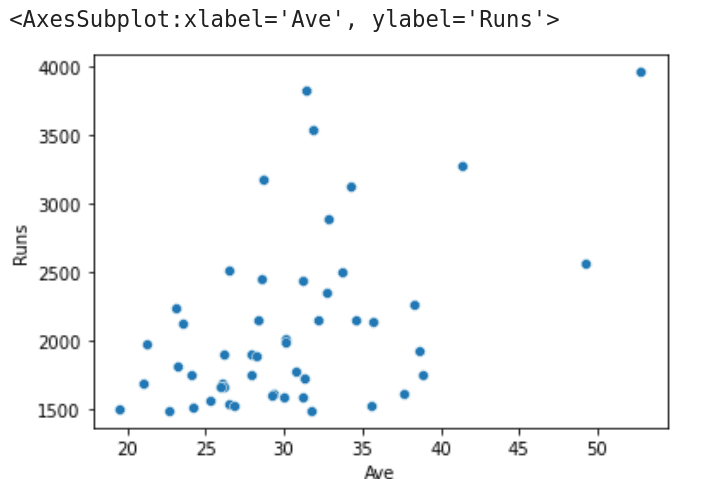圖 2：seaborn 繪制的散點圖

在程序末尾添加如下代碼行并再次運行。

sns.kdeplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)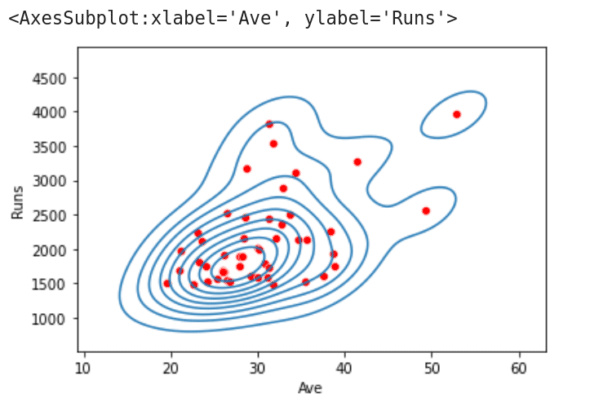

圖 3：使用 seaborn 繪制的核密度估計圖

這行代碼調用 kdeplot() 函數繪制第 5 列和第 7 列數據的 核密度估計Kernel Distribution Estimation（KDE）圖。KDE 圖可以描述連續或非參數數據變量的概率密度函數。這個定義可能無法讓您了解函數 kdeploy() 將要執行的實際操作。圖 3 是在單個圖像上繪制的 KDE 圖和散點圖。從圖中我們可以看到，散點圖繪制的數據點被 KDE 圖分組成簇。seaborn 還提供了許多其他繪圖功能。在圖 1 中程序的第 7 行分別替換為下面的的代碼行（一次一行），并再次執行該程序，你會看到不同風格的繪圖顯示。探索 seaborn 提供的其他繪圖功能，并選擇最適合你需求的功能。

sns.histplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)
sns.rugplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)

更多概率論

在本系列之前的一篇文章中，我們看到可以用正態分布來對現實場景進行建模。但正態分布只是眾多重要概率分布中的一種。圖 4 中的程序繪制了三種概率分布。

圖 4：繪制多種概率分布的程序

下面我來解釋這個程序。第 1 行導入 NumPy 的 random 模塊。第 2 行和第 3 行導入用于繪圖的 Matplotlib 和 seaborn。第 5 行生成帶有參數 n（試驗次數）和 p（成功概率）的 二項分布binomial distribution數據。

二項分布是一種離散概率分布，它給出了在一系列 n 次獨立實驗中成功的數量。第三個參數 size 決定了輸出的形狀。第 6 行繪制生成的數據的直方圖。由于參數 kde=True，它還會繪制 KDE 圖。第三個參數 color='r' 表示繪圖時使用紅色。第 7 行生成一個泊松分布。泊松分布是一種離散概率分布，它給出了二項分布的極限。參數 lam 表示在固定時間間隔內發生預期事件的次數。這里的參數 size 也決定了輸出的形狀。第 8 行將生成的數據繪制為綠色的直方圖。第 9 行生成大小為 1000 的指數分布。第 10 行將生成的數據繪制為藍色的直方圖。最后，第 11 繪制三個概率分布的所有圖像（見圖 5）。NumPy 的 random 模塊提供了大量的其他概率分布，如 Dirichlet 分布、Gamma 分布、幾何分布、拉普拉斯分布等。學習和熟悉它們將是非常值得的。

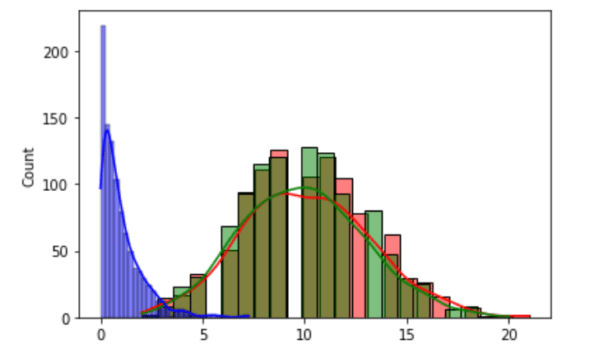圖 5：概率分布的圖像

現在，讓我們學習線性回歸。使用線性回歸分析可以根據一個變量來預測一個變量的值。線性回歸的一個重要應用是數據擬合。線性回歸非常重要，因為它很簡單。機器學習中的監督學習范式實際上就是回歸建模。因此，線性回歸可以被認為是一種重要的機器學習策略。這種學習范式通常被統計學家稱為統計學習。線性回歸是機器學習中的重要操作。NumPy 和 SciPy 都提供了線性回歸的函數。下面我們展示使用 NumPy 和 SciPy 進行線性回歸的示例。

圖 6：使用 NumPy 進行線性回歸

圖 6 是使用 NumPy 進行線性回歸的程序。第 1 行和第 2 行導入 NumPy 和 Matplotlib。第 4 行和第 5 行初始化變量 a和 b。第 6 行使用函數 linspace() 在 0 和 1 之間等間隔地生成 100 個數字。第 7 行使用變量 a、b 和數組 x 生成數組 y 中的值。函數 randn() 返回標準正態分布的數據。第 8 行將數組 x 和 y 中的值繪制成散點圖（見圖 7），圖中的 100 個數據點用紅色標記。第 9 行使用函數 polyfit() 執行稱為 最小二乘多項式擬合least squares polynomial fit 的線性回歸技術。函數 polyfit() 的輸入參數包括數組 x 和 y，以及第三個表示擬合多項式的階數的參數，在本例中為 1，表示擬合一條直線。該函數的返回值是多項式的系數，代碼中將其存儲在數組 p 中。第 10 行使用函數 polyval() 對多項式求值，并將這些值存儲在數組y_l中。第 11 行用藍色繪制擬合得到的直線（見圖 7）。最后，第 12 行顯示所有的圖像。可以用這條回歸直線預測可能的 (x, y) 數據對。

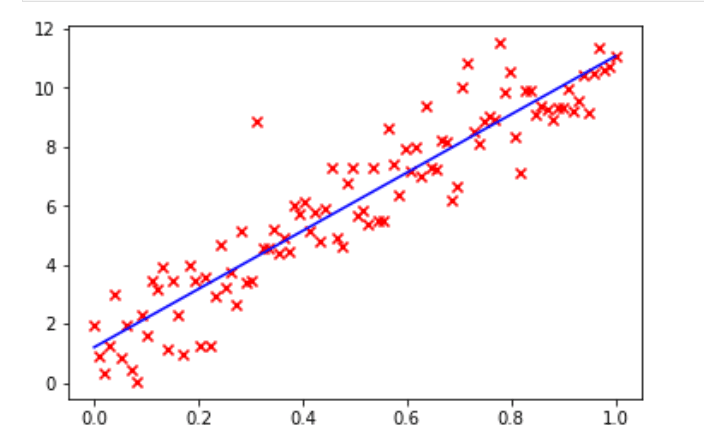圖 7：線性回歸散點圖 1

圖 8 是使用 SciPy 進行線性回歸的程序代碼。

圖 8：使用 SciPy 進行線性回歸

下面我解釋一下這個程序的工作原理。第 1 行和第 2 行導入庫 NumPy 和 Matplotlib。第 3 行從庫 SciPy 導入 stats 模塊。第 4 到 8 行與前面的程序執行類似的任務。第 9 行使用 SciPy 的 stats 模塊的 linregression() 函數計算兩組測量值的線性最小二乘回歸——在本例中是數組 x 和 y 中的值。該函數返回值中的 m 和 c 分別表示回歸直線的 斜率slope和截距intercept。第 10 行使用斜率和截距的值生成回歸線。第 11 行用綠色繪制回歸線。最后，第 12 行顯示所有的圖像（見圖 9），其中數據點以黃色顯示，回歸線以綠色顯示。

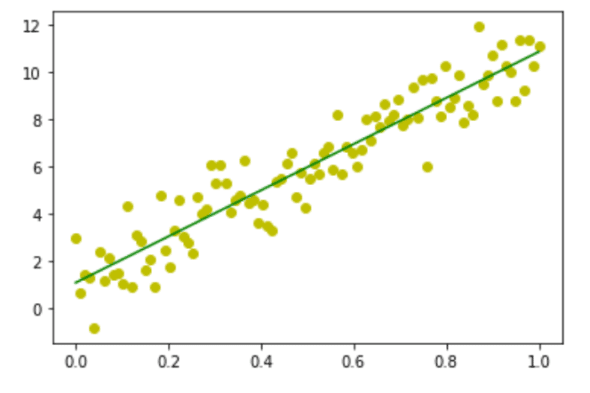圖 9：線性回歸散點圖 2

在本系列的前面幾篇文章中，我們學習了概率和統計學的一些概念。盡管還不夠全面的，但我認為這已經打下了一個良好的基礎，現在是時候將注意力轉移到其他同樣重要的問題上了。

Keras 簡介

Keras 一般與 TensorFlow 一起使用。因此，我們先從使用 TensorFlow 開始。圖 10 所示的程序雖然只包含四行代碼，但確實構建了在本系列中的第一個神經網絡。下面我來介紹它的工作原理。第 1 行導入庫 TensorFlow。第 2 行創建了一個名為 x 的張量。第 3 行和第 4 行分別在張量 x 上應用 ReLU（整流線性單元Rectified Linear Unit）和 Leaky ReLU 激活函數。在神經網絡中，激活函數定義了節點的輸出由輸入計算出的規則。ReLU 激活函數是定義為 Relu(x) = max(0,x)。第 3 行代碼的輸出如圖 10 所示。可以觀察到，在應用 ReLU 激活函數后，張量 x 中的負值被替換為零。Leaky ReLU 是 ReLU 激活函數的改進版本。從圖 10 中的第 4 行代碼的輸出可以看出 Leaky ReLU 激活函數保留了全量的正值和 20% 的負值。在后面我們將會繼續討論 Keras，同時學習更多神經網絡和激活函數的知識。

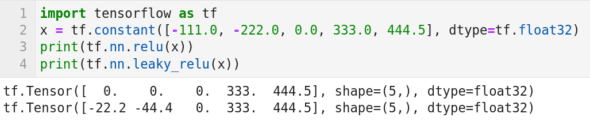圖 10：使用 TensorFlow 實現的神經網絡

下面我們開始使用 Keras。Keras 的安裝也可以通過 Anaconda Navigator 輕松完成。圖 11 所示的程序導入了我們的第一個數據集并顯示了其中的一個數據樣本。在下一篇文章中，我們將使用這個數據集來訓練和測試模型，從而開啟我們開發人工智能和機器學習程序的下一個階段。

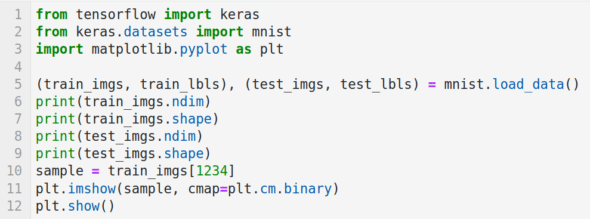圖 11：第一個數據集

下面介紹這個程序的工作原理。第 1 行導入 Keras。第 2 行從 Keras 導入手寫數字數據集 MNIST。它包含 6 萬個訓練樣本和 1 萬個測試樣本。第 3 行導入 Matplotlib。第 5 行加載 MNIST 數據集。第 6 到 9 行打印訓練集和測試集的維數和維度。圖 12 顯示了這些代碼行的輸出。可以看出，訓練集和測試集都是三維的，所有數據樣本的分辨率都是 28 × 28。第 10 行加載了第 1234 個訓練圖像。第 11 行和第 12 行顯示這個圖像。從圖 12 可以看到它是數字 3 的手寫圖像。

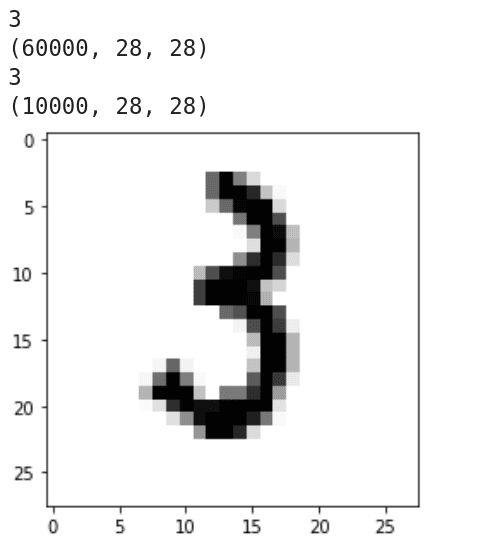圖 12：數據樣例

本文中我們開始涉及到神經網絡，并通過 Keras 接觸到了第一個數據集。在下一篇文章中，我們將繼續講解神經網絡和 Keras，并通過使用該數據集訓練自己的模型。我們還會遇到 scikit-learn, 它是另一個強大的機器學習 Python 庫 。