使用PyTorch實現混合專家(MoE)模型
Mixtral 8x7B 的推出在開放 AI 領域引發了廣泛關注,特別是混合專家(Mixture-of-Experts:MoEs)這一概念被大家所認知。混合專家(MoE)概念是協作智能的象征,體現了“整體大于部分之和”的說法。MoE模型匯集了各種專家模型的優勢,以提供更好的預測。它是圍繞一個門控網絡和一組專家網絡構建的,每個專家網絡都擅長特定任務的不同方面
在本文中,我將使用Pytorch來實現一個MoE模型。在具體代碼之前,讓我們先簡單介紹一下混合專家的體系結構。
MoE架構
MoE由兩種類型的網絡組成:(1)專家網絡和(2)門控網絡。
專家網絡:專家網絡是專有模型,每個模型都經過訓練,在數據的一個子集中表現出色。MoE的理念是擁有多名優勢互補的專家,確保對問題空間的全面覆蓋。
門控網絡:門控網絡充當指揮,協調或管理個別專家的貢獻。它學習(或權衡)哪個網絡擅長處理哪種類型的輸入。經過訓練的門控網絡可以評估新的輸入向量,并根據專家的熟練程度將處理責任分配給最合適的專家或專家組合。門控網絡根據專家的輸出與當前輸入的相關性動態調整其權重,確保定制響應。
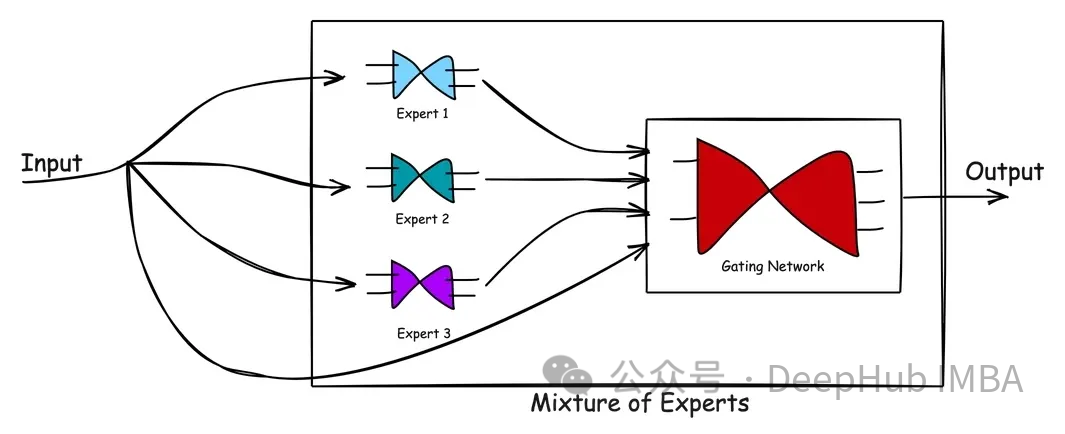
上圖顯示了MoE中的處理流程。混合專家模型的優點在于它的簡單。通過學習復雜的問題空間以及專家在解決問題時的反應,MoE模型有助于產生比單個專家更好的解決方案。門控網絡作為一個有效的管理者,評估情景并將任務傳遞給最佳專家。當新數據輸入時,模型可以通過重新評估專家對新輸入的優勢來適應,從而產生靈活的學習方法。
MoE為部署機器學習模型提供了巨大的好處。以下是兩個顯著的好處。
MoE的核心優勢在于其專家網絡的多元化和專業化。MoE的設置能夠以單一模型可能難以達到的精度處理多方面的問題。
MoE具有固有的可伸縮性。隨著任務復雜性的增加,可以在不改變其他專家模型的情況下將更多專家無縫地集成到系統中,擴大專業知識的范圍。也就是說,MoE可以幫助將預先訓練過的專家打包到機器學習系統中。
混合專家模型在許多領域都有應用,包括推薦系統、語言建模和各種復雜的預測任務。有傳言稱,GPT-4是由多個專家組成的。盡管我們無法確認,但類似gpt -4的模型將通過MoE方法利用多個模型的力量來提供最佳結果。
Pytorch代碼
我們這里不討論Mixtral 8x7B這種大模型中使用的MOE技術,而是我們編寫一個簡單的、可以應用在任何任務中的自定義MOE,通過代碼我們可以了解MOE的工作原理,這樣對理解MOE在大模型中的工作方式是非常有幫助的。
下面我們將一段一段地介紹PyTorch的代碼實現。
導入庫:
import torch
import torch.nn as nn
import torch.optim as optim定義專家模型:
class Expert(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(Expert, self).__init__()
self.layer1 = nn.Linear(input_dim, hidden_dim)
self.layer2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = torch.relu(self.layer1(x))
return torch.softmax(self.layer2(x), dim=1)這里我們定義了一個簡單的專家模型,可以看到它是一個2層的mlp,使用了relu激活,最后使用softmax輸出分類概率。
定義門控模型:
# Define the gating model
class Gating(nn.Module):
def __init__(self, input_dim,
num_experts, dropout_rate=0.1):
super(Gating, self).__init__()
# Layers
self.layer1 = nn.Linear(input_dim, 128)
self.dropout1 = nn.Dropout(dropout_rate)
self.layer2 = nn.Linear(128, 256)
self.leaky_relu1 = nn.LeakyReLU()
self.dropout2 = nn.Dropout(dropout_rate)
self.layer3 = nn.Linear(256, 128)
self.leaky_relu2 = nn.LeakyReLU()
self.dropout3 = nn.Dropout(dropout_rate)
self.layer4 = nn.Linear(128, num_experts)
def forward(self, x):
x = torch.relu(self.layer1(x))
x = self.dropout1(x)
x = self.layer2(x)
x = self.leaky_relu1(x)
x = self.dropout2(x)
x = self.layer3(x)
x = self.leaky_relu2(x)
x = self.dropout3(x)
return torch.softmax(self.layer4(x), dim=1)門控模型更復雜,有三個線性層和dropout層用于正則化以防止過擬合。它使用ReLU和LeakyReLU激活函數引入非線性。最后一層的輸出大小等于專家的數量,并對這些輸出應用softmax函數。輸出權重,這樣可以將專家的輸出與之結合。
說明:其實門控網絡,或者叫路由網絡是MOE中最復雜的部分,因為它涉及到控制輸入到那個專家模型,所以門控網絡也有很多個設計方案,例如(如果我沒記錯的話)Mixtral 8x7B 只是取了8個專家中的top2。所以我們這里不詳細討論各種方案,只是介紹其基本原理和代碼實現。
完整的MOE模型:
class MoE(nn.Module):
def __init__(self, trained_experts):
super(MoE, self).__init__()
self.experts = nn.ModuleList(trained_experts)
num_experts = len(trained_experts)
# Assuming all experts have the same input dimension
input_dim = trained_experts[0].layer1.in_features
self.gating = Gating(input_dim, num_experts)
def forward(self, x):
# Get the weights from the gating network
weights = self.gating(x)
# Calculate the expert outputs
outputs = torch.stack(
[expert(x) for expert in self.experts], dim=2)
# Adjust the weights tensor shape to match the expert outputs
weights = weights.unsqueeze(1).expand_as(outputs)
# Multiply the expert outputs with the weights and
# sum along the third dimension
return torch.sum(outputs * weights, dim=2)這里主要看前向傳播的代碼,通過輸入計算出權重和每個專家給出輸出的預測,最后使用權重將所有專家的結果求和最終得到模型的輸出。
這個是不是有點像“集成學習”。
測試
下面我們來對我們的實現做個簡單的測試,首先生成一個簡單的數據集:
# Generate the dataset
num_samples = 5000
input_dim = 4
hidden_dim = 32
# Generate equal numbers of labels 0, 1, and 2
y_data = torch.cat([
torch.zeros(num_samples // 3),
torch.ones(num_samples // 3),
torch.full((num_samples - 2 * (num_samples // 3),), 2) # Filling the remaining to ensure exact num_samples
]).long()
# Biasing the data based on the labels
x_data = torch.randn(num_samples, input_dim)
for i in range(num_samples):
if y_data[i] == 0:
x_data[i, 0] += 1 # Making x[0] more positive
elif y_data[i] == 1:
x_data[i, 1] -= 1 # Making x[1] more negative
elif y_data[i] == 2:
x_data[i, 0] -= 1 # Making x[0] more negative
# Shuffle the data to randomize the order
indices = torch.randperm(num_samples)
x_data = x_data[indices]
y_data = y_data[indices]
# Verify the label distribution
y_data.bincount()
# Shuffle the data to ensure x_data and y_data remain aligned
shuffled_indices = torch.randperm(num_samples)
x_data = x_data[shuffled_indices]
y_data = y_data[shuffled_indices]
# Splitting data for training individual experts
# Use the first half samples for training individual experts
x_train_experts = x_data[:int(num_samples/2)]
y_train_experts = y_data[:int(num_samples/2)]
mask_expert1 = (y_train_experts == 0) | (y_train_experts == 1)
mask_expert2 = (y_train_experts == 1) | (y_train_experts == 2)
mask_expert3 = (y_train_experts == 0) | (y_train_experts == 2)
# Select an almost equal number of samples for each expert
num_samples_per_expert = \
min(mask_expert1.sum(), mask_expert2.sum(), mask_expert3.sum())
x_expert1 = x_train_experts[mask_expert1][:num_samples_per_expert]
y_expert1 = y_train_experts[mask_expert1][:num_samples_per_expert]
x_expert2 = x_train_experts[mask_expert2][:num_samples_per_expert]
y_expert2 = y_train_experts[mask_expert2][:num_samples_per_expert]
x_expert3 = x_train_experts[mask_expert3][:num_samples_per_expert]
y_expert3 = y_train_experts[mask_expert3][:num_samples_per_expert]
# Splitting the next half samples for training MoE model and for testing
x_remaining = x_data[int(num_samples/2)+1:]
y_remaining = y_data[int(num_samples/2)+1:]
split = int(0.8 * len(x_remaining))
x_train_moe = x_remaining[:split]
y_train_moe = y_remaining[:split]
x_test = x_remaining[split:]
y_test = y_remaining[split:]
print(x_train_moe.shape,"\n", x_test.shape,"\n",
x_expert1.shape,"\n",
x_expert2.shape,"\n", x_expert3.shape)這段代碼創建了一個合成數據集,其中包含三個類標簽——0、1和2。基于類標簽對特征進行操作,從而在數據中引入一些模型可以學習的結構。
數據被分成針對個別專家的訓練集、MoE模型和測試集。我們確保專家模型是在一個子集上訓練的,這樣第一個專家在標簽0和1上得到很好的訓練,第二個專家在標簽1和2上得到更好的訓練,第三個專家看到更多的標簽2和0。
我們期望的結果是:雖然每個專家對標簽0、1和2的分類準確率都不令人滿意,但通過結合三位專家的決策,MoE將表現出色。
模型初始化和訓練設置:
# Define hidden dimension
output_dim = 3
hidden_dim = 32
epochs = 500
learning_rate = 0.001
# Instantiate the experts
expert1 = Expert(input_dim, hidden_dim, output_dim)
expert2 = Expert(input_dim, hidden_dim, output_dim)
expert3 = Expert(input_dim, hidden_dim, output_dim)
# Set up loss
criterion = nn.CrossEntropyLoss()
# Optimizers for experts
optimizer_expert1 = optim.Adam(expert1.parameters(), lr=learning_rate)
optimizer_expert2 = optim.Adam(expert2.parameters(), lr=learning_rate)
optimizer_expert3 = optim.Adam(expert3.parameters(), lr=learning_rate)實例化了專家模型和MoE模型。定義損失函數來計算訓練損失,并為每個模型設置優化器,在訓練過程中執行權重更新。
訓練的步驟也非常簡單
# Training loop for expert 1
for epoch in range(epochs):
optimizer_expert1.zero_grad()
outputs_expert1 = expert1(x_expert1)
loss_expert1 = criterion(outputs_expert1, y_expert1)
loss_expert1.backward()
optimizer_expert1.step()
# Training loop for expert 2
for epoch in range(epochs):
optimizer_expert2.zero_grad()
outputs_expert2 = expert2(x_expert2)
loss_expert2 = criterion(outputs_expert2, y_expert2)
loss_expert2.backward()
optimizer_expert2.step()
# Training loop for expert 3
for epoch in range(epochs):
optimizer_expert3.zero_grad()
outputs_expert3 = expert3(x_expert3)
loss_expert3 = criterion(outputs_expert3, y_expert3)
loss_expert3.backward()每個專家使用基本的訓練循環在不同的數據子集上進行單獨的訓練。循環迭代指定數量的epoch。
下面是我們MOE的訓練
# Create the MoE model with the trained experts
moe_model = MoE([expert1, expert2, expert3])
# Train the MoE model
optimizer_moe = optim.Adam(moe_model.parameters(), lr=learning_rate)
for epoch in range(epochs):
optimizer_moe.zero_grad()
outputs_moe = moe_model(x_train_moe)
loss_moe = criterion(outputs_moe, y_train_moe)
loss_moe.backward()
optimizer_moe.step()MoE模型是由先前訓練過的專家創建的,然后在單獨的數據集上進行訓練。訓練過程類似于單個專家的訓練,但現在門控網絡的權值在訓練過程中更新。
最后我們的評估函數:
# Evaluate all models
def evaluate(model, x, y):
with torch.no_grad():
outputs = model(x)
_, predicted = torch.max(outputs, 1)
correct = (predicted == y).sum().item()
accuracy = correct / len(y)
return accuracyevaluate函數計算模型在給定數據上的精度(x代表樣本,y代表預期標簽)。準確度計算為正確預測數與預測總數之比。
結果如下:
accuracy_expert1 = evaluate(expert1, x_test, y_test)
accuracy_expert2 = evaluate(expert2, x_test, y_test)
accuracy_expert3 = evaluate(expert3, x_test, y_test)
accuracy_moe = evaluate(moe_model, x_test, y_test)
print("Expert 1 Accuracy:", accuracy_expert1)
print("Expert 2 Accuracy:", accuracy_expert2)
print("Expert 3 Accuracy:", accuracy_expert3)
print("Mixture of Experts Accuracy:", accuracy_moe)
#Expert 1 Accuracy: 0.466
#Expert 2 Accuracy: 0.496
#Expert 3 Accuracy: 0.378
#Mixture of Experts Accuracy: 0.614可以看到
專家1正確預測了測試數據集中大約46.6%的樣本的類標簽。
專家2表現稍好,正確預測率約為49.6%。
專家3在三位專家中準確率最低,正確預測的樣本約為37.8%。
而MoE模型顯著優于每個專家,總體準確率約為61.4%。
總結
我們測試的輸出結果顯示了混合專家模型的強大功能。該模型通過門控網絡將各個專家模型的優勢結合起來,取得了比單個專家模型更高的精度。門控網絡有效地學習了如何根據輸入數據權衡每個專家的貢獻,以產生更準確的預測。混合專家利用了各個模型的不同專業知識,在測試數據集上提供了更好的性能。
同時也說明我們可以在現有的任務上嘗試使用MOE來進行測試,也可以得到更好的結果。









































