在大模型領域，Transformer 憑一己之力撐起了整個江山。但隨著模型規模的擴展和需要處理的序列不斷變長，Transformer 的局限性也逐漸凸顯，比如其自注意力機制的計算量會隨著上下文長度的增加呈平方級增長。為了克服這些缺陷，研究者們開發出了很多注意力機制的高效變體，但收效甚微。

最近，一項名為「Mamba」的研究似乎打破了這一局面，它在語言建模方面可以媲美甚至擊敗 Transformer。這都要歸功于作者提出的一種新架構 —— 選擇性狀態空間模型（ selective state space model），該架構是 Mamba 論文作者 Albert Gu 此前主導研發的 S4 架構（Structured State Spaces for Sequence Modeling ）的一個簡單泛化。

在 Mamba 論文發布后，很多研究者都對 SSM（state space model）、S4 等相關研究產生了好奇。其中，有位研究者表示自己要在飛機上把這些論文都讀一下。對此，Albert Gu 給出了更好的建議：他的博士論文其實把這些進展都梳理了一下，讀起來可能更有條理。

在論文摘要中，作者寫到，序列模型是深度學習模型的支柱，已在科學應用領域取得了廣泛成功。然而，現有的方法需要針對不同的任務、模態和能力進行廣泛的專業化；存在計算效率瓶頸；難以對更復雜的序列數據（如涉及長依賴關系時）進行建模。因此，繼續開發對一般序列進行建模的原則性和實用性方法仍然具有根本性的重要意義。

論文鏈接：https://stacks.stanford.edu/file/druid:mb976vf9362/gu_dissertation-augmented.pdf

作者在論文中闡述了一種使用狀態空間模型進行深度序列建模的新方法，這是一種靈活的方法，具有理論基礎，計算效率高，并能在各種數據模態和應用中取得強大的結果。

首先，作者介紹了一類具有眾多表征和屬性的模型，它們概括了標準深度序列模型（如循環神經網絡和卷積神經網絡）的優勢。然而，作者表明計算這些模型可能具有挑戰性，并開發了在當前硬件上運行非常快速的新型結構化狀態空間，無論是在擴展到長序列時還是在自回歸推理等其他設置中都是如此。最后，他們提出了一個用于對連續信號進行增量建模的新穎數學框架，該框架可與狀態空間模型相結合，為其賦予原則性的狀態表示，并提高其對長程依賴關系的建模能力。總之，這一類新方法為機器學習模型提供了有效而多用途的構建模塊，特別是在大規模處理通用序列數據方面。

以下是論文各部分簡介。

深度序列模型

針對序列數據的深度學習模型可被視為圍繞循環、卷積或注意力等簡單機制建立的序列到序列轉換。

這些基元（primitive）可以被納入標準的深度神經網絡架構，形成主要的深度序列模型系列：循環神經網絡（RNN）、卷積神經網絡（CNN）和 Transformers，它們表達了強大的參數化變換，可以使用標準的深度學習技術（如梯度下降反向傳播）進行學習。圖 1.1 和定義 1.1 展示了本論文中使用的序列模型抽象，第 2.1 節將結合實例對其進行更正式的定義。

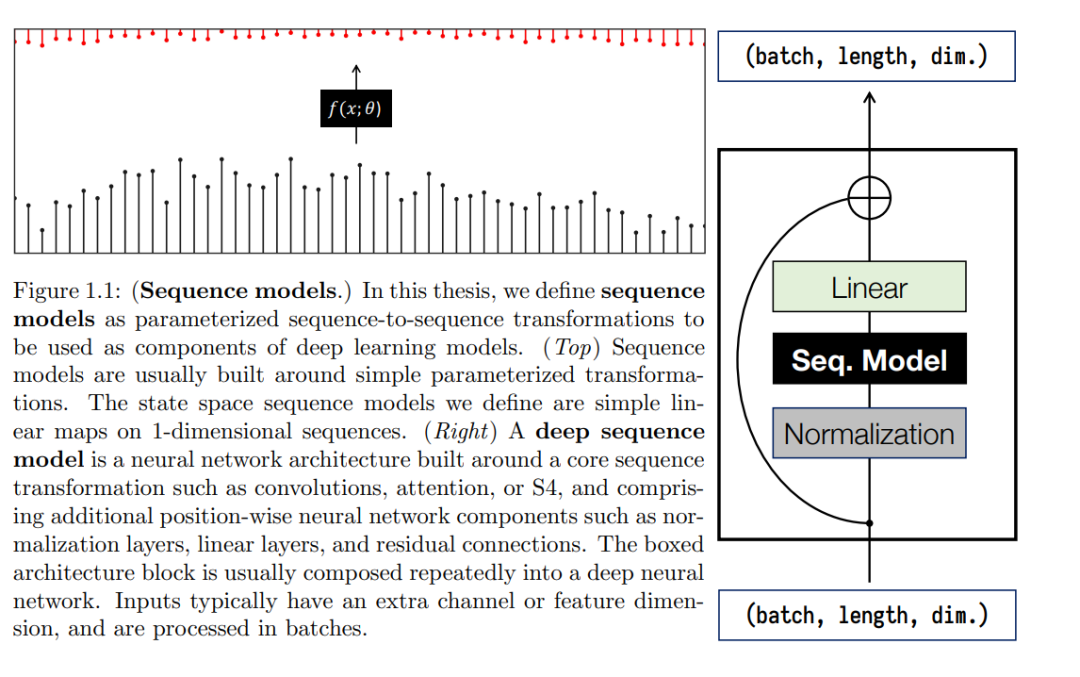
定義 1.1（非正式）。作者使用序列模型來指代在序列 y = f_θ(x) 上的參數化映射，其中輸入和輸出 x、y 是 R^D 中長度為 L 的特征向量序列，θ 是通過梯度下降學習的參數。

上述每個模型系列都為機器學習帶來了巨大的成功：例如，RNN 為機器翻譯帶來了深度學習，CNN 是第一個神經音頻生成模型，而 Transformers 則徹底改變了 NLP 的廣闊領域。

不過，這些模型也有其序列機制所遺留的折衷問題。例如，RNN 對于序列數據來說是一個天然的有狀態模型，每個時間步只需要恒定的計算 / 存儲，但訓練速度慢，而且存在優化困難（如梯度消失問題），這限制了它們處理長序列的能力。CNN 專注于局部上下文，編碼 shift equivariance 等特性，并具有快速、可并行訓練的特點，但其序列推理成本較高，且上下文長度受到固有限制。Transformers 因其處理長程依賴關系的能力和可并行性而獲得巨大成功，但在序列長度上存在二次擴展問題。另一個最新的模型系列是神經微分方程（NDE），這是一種有理論基礎的數學模型，理論上可以解決連續時間問題和長期依賴關系，但效率非常低。

這些問題顯示了深度序列模型面臨的三大挑戰。

挑戰一：通用能力

深度學習的一個廣泛目標是開發可用于各種問題的通用構建模塊。序列模型為解決許多此類問題提供了一個通用框架。它們可以應用于任何可被投射為序列的環境。然而，當前的模型通常仍需要大量的專業化能力，以解決特定任務和領域的問題，或針對特定的能力。各類模型的優勢分析如下：

• RNN：需要快速更新隱藏狀態的有狀態設置，例如在線處理任務和強化學習；
• CNN：對音頻、圖像和視頻等均勻采樣的感知信號進行建模；
• Transformers：對語言等領域中密集、復雜的交互進行建模；
• NDE：處理非典型時間序列設置，如缺失或不規則采樣數據。

反之，每個模型系列都可能在其不擅長的功能方面舉步維艱。

挑戰二：計算效率

在實踐中應用深度序列模型需要計算其定義的函數（即參數化序列到序列映射），這可以有多種形式。在訓練時，任務一般可以用整個輸入序列的損失函數來表述，算法的核心問題是如何高效地計算前向傳遞。在推理時（訓練完成后部署模型），設置可能會發生變化；例如，在在線處理或自回歸生成設置中，輸入每次只顯示一個時間步，模型必須能夠高效地按順序處理這些輸入。

這兩種情況對不同的模型系列都提出了挑戰。例如，RNN 本身是序列性的，很難在 GPU 和 TPU 等現代硬件加速器上進行訓練，而并行性則能使其受益。另一方面，CNN 和 Transformers 則難以進行高效的自回歸推理，因為它們不是有狀態的；處理單個新輸入的成本可能會與模型的整個上下文大小成比例關系。更奇特的模型可能會帶來額外的功能，但通常會使其計算更加困難和緩慢（如需要調用昂貴的微分方程求解器）。

挑戰三：長程依賴

現實世界中的序列數據可能需要推理數以萬計的時間步驟。除了處理長輸入所需的計算問題外，解決這一問題還需要能夠對此類長程依賴（LRD）中存在的復雜交互進行建模。具體來說，困難可能來自于無法捕捉數據中的交互，比如模型的上下文窗口有限；也可能來自于優化問題，比如在循環模型中通過長計算圖進行反向傳播時的梯度消失問題。

由于效率、表達能力或訓練能力方面的限制，長程依賴是序列模型長期以來面臨的挑戰。所有標準模型系列，如 NDE、RNN、CNN 和 Transformers，都包括許多旨在解決這些問題的專門變體。例如對抗梯度消失的正交和 Lipschitz RNN、增加上下文大小的空洞卷積，以及日益龐大的高效注意力變體系列，這些變體降低了對序列長度的二次依賴。然而，盡管這些解決方案都是針對長程依賴設計的，但在 Long Range Arena 等具有挑戰性的基準測試中，它們的表現仍然不佳。

 狀態空間序列模型

本論文介紹了基于線性狀態空間模型（SSM）的新系列深度序列模型。作者將 SSM 定義為一個簡單的序列模型，它通過一個隱式的潛在狀態 x (t)∈R^N 映射一個 1 維函數或序列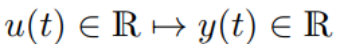 

SSM 是一種基礎科學模型，廣泛應用于控制論、計算神經科學、信號處理等領域。廣義上，SSM 一詞指的是對潛變量如何在狀態空間中演化進行建模的任何模型。這些廣義的 SSM 有許多種，可以改變 x 的狀態空間（如連續、離散或混合空間）、y 的觀測空間、過渡動態、附加噪聲過程或系統的線性度。SSM 在歷史上通常指隱馬爾可夫模型（HMM）和線性動力系統（LDS）的變體，如分層狄利克雷過程（HDP-HMM）和 Switching Linear Dynamical 系統（SLDS）。

方程（1.1）的狀態空間模型在狀態空間和動力學上都是連續的，并且是完全線性和確定性的，但還沒有被用作定義 1.1 意義上的深度序列模型。本論文探討了狀態空間序列模型的諸多優點，以及如何利用它們來解決一般序列建模難題，同時克服其自身的局限性。

通用序列模型

SSM 是一種簡單而基本的模型，具有許多豐富的特性。它們與 NDE、RNN 和 CNN 等模型族密切相關，實際上可以以多種形式編寫，以實現通常需要專門模型才能實現的各種功能（挑戰一）。

• SSM 是連續的。SSM 本身是一個微分方程。因此，它可以執行連續時間模型的獨特應用，如模擬連續過程、處理缺失數據，以及適應不同的采樣率。
• SSM 是循環的。可以使用標準技術將 SSM 離散化為線性 recurrence，并在推理過程中模擬為狀態循環模型，每個時間步的內存和計算量保持不變。
• SSM 是卷積系統。SSM 是線性時不變系統，可顯式表示為連續卷積。此外，離散時間版本可以在使用離散卷積進行訓練時并行化，從而實現高效訓練。

因此，SSM 是一種通用序列模型，在并行和序列環境以及各種領域（如音頻、視覺、時間序列）中都能高效運行。論文第 2 章介紹了 SSM 的背景，并闡述了狀態空間序列模型的這些特性。

不過，SSM 的通用性也有代價。原始 SSM 仍然面臨兩個額外挑戰 —— 也許比其他模型更嚴重 —— 這阻礙了它們作為深度序列模型的使用。挑戰包括：（1）一般 SSM 比同等大小的 RNN 和 CNN 慢得多；（2）它們在記憶長依賴關系時會很吃力，例如繼承了 RNN 的梯度消失問題。

作者通過 SSM 的新算法和理論來應對這些挑戰。

利用結構化 SSM 進行高效計算（S4）

遺憾的是，由于狀態表示 x (t) ∈ R^N 對計算和內存的要求過高（挑戰二），通用的 SSM 在實踐中無法用作深度序列模型。

對于 SSM 的狀態維度 N 和序列長度 L，僅計算完整的潛在狀態 x 就需要 O (N^2L) 次運算和 O (NL) 的空間 —— 與計算總體輸出的 Ω(L + N) 下界相比。因此，對于合理大小的模型（例如 N ≈ 100），SSM 使用的內存要比同等大小的 RNN 或 CNN 多出幾個數量級，因此作為通用序列建模解決方案，SSM 在計算上是不切實際的。

要克服這一計算瓶頸，就必須以一種適合高效算法的方式對狀態矩陣 A 施加結構。作者介紹了具有各種形式結構矩陣 A 的結構化狀態空間序列模型（S4）（或簡稱結構化狀態空間）家族，以及能以任何表示形式（如循環或卷積）高效計算 S4 模型的新算法。

論文第 3 章介紹了這些高效 S4 模型的不同類型。第一種結構使用狀態矩陣的對角參數化（diagonal parameterization），它非常簡單、通用，足以表示幾乎所有的 SSM。然后，作者通過允許低秩校正項對其進行推廣，這對于捕捉后面介紹的一類特殊的 SSM 是必要的。通過結合眾多技術思想，如生成函數、線性代數變換和結構矩陣乘法的結果，作者為這兩種結構開發了時間復雜度為 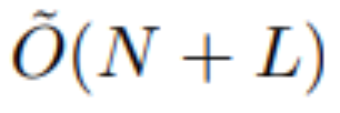 和空間復雜度為 O (N + L) 的算法，這對于序列模型來說基本上是嚴密的。

使用 HIPPO 解決長程依賴關系

即使不考慮計算問題，基本的 SSM 在實驗中仍然表現不佳，而且無法建模長程依賴關系（挑戰三）。直觀地說，其中一種解釋是線性一階 ODE 求解為指數函數，因此可能會出現梯度隨序列長度呈指數級縮放的問題。這也可以從它們作為線性 recurrence 的解釋中看出，這涉及到反復對一個 recurrent 矩陣進行冪運算，這就是眾所周知的 RNN 梯度消失/爆炸問題的起因。

在第 4 章中，作者從 SSM 后退一步，轉而研究如何從第一性原理出發，用循環模型對 LRD 進行建模。他們開發了一個名為 HIPPO 的數學框架，它形式化并解決了一個名為在線函數逼近（或記憶）的問題。這種方法旨在通過保持對連續函數歷史的壓縮，以逐步記憶連續函數。盡管這些方法的動機完全獨立，但它們都是 SSM 的具體形式。這些最終的方法被證明是 SSM 的特定形式 —— 盡管它們的動機是完全獨立的。

論文第 5 章完善了這一框架，并將其與 SSM 抽象更嚴格地聯系起來。它引入了一個正交 SSM 概念，廣泛推廣了 HIPPO，并推導出更多實例和理論結果，例如如何以原則性的方式初始化所有 SSM 參數。

HIPPO 概覽

考慮一個輸入函數 u (t)、一個固定的概率度量 ω(t)，以及 N 個正交基函數（如多項式）組成的序列。在每個時間 t，u 在時間 t 之前的歷史都可以投影到這個基上，從而得到一個系數向量 x (t)∈ R^N，這個向量代表了 u 的歷史相對于所提供的度量 ω 的最佳近似值。函數 u (t)∈R 映射到系數 x (t)∈R^N 的映射被稱為關于度量 ω 的高階多項式投影算子 （HIPPO）。在很多情況下，在許多情況下，其形式為 x ′ (t) = Ax (t) + Bu (t)，對于 (A, B) 有封閉形式的公式。

HIPPO 和 S4 的組合

HIPPO 提供了一個數學工具來構建具有重要屬性的 SSM，而 S4 是關于計算表示的。第 6 章正式將兩者聯系起來，并說明它們可以結合起來，以獲得兩個世界的最佳效果。論文表明，HIPPO 生成的用于處理長程依賴關系的特殊矩陣實際上可以用第 3 章中開發的特定結構形式來編寫。這就提供了結合 HIPPO 的 S4 的具體實例，從而產生了一個具有豐富功能、非常高效并擅長長程推理的通用序列模型。

應用、消融和擴展

通用序列建模功能

第 7 章對 S4 方法在各種領域和任務中的應用進行了全面的實證驗證。當 S4 方法被納入一個通用的簡單深度神經網絡時，它在許多基準測試中推進了 SOTA。

特別的亮點和功能包括：  

• 通用序列建模。在不改變架構的情況下，S4 在語音分類方面超越了音頻 CNN，在時間序列預測問題上優于專門的 Informer 模型，在序列 CIFAR 方面與 2-D ResNet 相媲美，準確率超過 90%。
• 長程依賴。在針對高效序列模型的 LRA 基準測試中，S4 的速度與所有基線一樣快，同時比所有 Transformer 變體的平均準確率高出 25% 以上。S4 是第一個解決了 LRA Path-X 任務（長度為 16384）這一難題的模型，準確率達到 96%，而之前所有工作的隨機猜測準確率僅為 50%。
• 采樣分辨率變化。與專門的 NDE 方法一樣，S4 無需再訓練即可適應時間序列采樣頻率的變化。
• 大規模生成建模與快速自回歸生成。在 CIFAR-10 密度估計方面，S4 與最好的自回歸模型（每維 2.85 比特）不相上下。在 WikiText-103 語言建模方面，S4 大幅縮小了與 Transformers 的差距（在 0.5 困惑度范圍內），在無注意力模型中實現了 SOTA。與 RNN 一樣，在 CIFAR-10/WikiText-103 上，S4 利用其潛在狀態生成像素 /token 的速度比標準自回歸模型快 60 倍。

理論消融

作者對 S4 的處理討論了訓練 SSM 的許多理論細節，例如如何仔細初始化每個參數以及如何納入 HIPPO 框架。他們對這些細節進行了全面的實證分析和消融研究，驗證了他們的 SSM 理論的各個方面。例如，他們驗證了 HIPPO 大大提高了 SSM 的建模能力，在標準序列模型基準上的性能比原始 SSM 實例提高了 15%。在算法上，他們的 S4 算法比傳統的 SSM 算法提高了幾個數量級（例如，速度提高了 30 倍，內存使用量減少到 1/400）。

應用：音頻波形生成

作為一種具有多種特性的序列建模基元，S4 可以被整合到不同的神經網絡架構中，并以多種方式使用。第 8 章介紹了 S4 在原始音頻波形生成中的應用，由于音頻波形的采樣率較高，這是一個具有挑戰性的問題。這一章節介紹了圍繞 S4 構建的 SaShiMi 多尺度架構，該架構在包括自回歸和擴散在內的多種生成建模范式中，推動了無限制音頻和語音生成技術的發展。該應用突顯了 S4 的靈活功能，包括高效訓練、快速自回歸生成和用于連續信號建模的強大歸納偏置。

擴展：用于計算機視覺的多維信號

雖然作者主要關注一維序列，但某些形式的數據本身具有更高的維度，如圖像（二維）和視頻（三維）。序列模型的靈活性也適用于這些環境。第 9 章介紹了 S4ND，這是 S4 從一維到多維（N-D）信號的擴展。S4ND 繼承了 S4 的特性，如直接對底層連續信號建模，并具有更好地處理輸入分辨率變化等相關優勢，是第一個在 ImageNet 等大型視覺任務中性能具有競爭力的連續模型。

更多細節請參考原論文。

最后，借機梳理介紹幾篇 SSM 研究，供大家了解、學習。

論文一：Pretraining Without Attention

• 論文地址：https://arxiv.org/pdf/2212.10544.pdf
• 機器之心報道：預訓練無需注意力，擴展到4096個token不成問題，與BERT相當

論文二：Mamba: Linear-Time Sequence Modeling with Selective State Spaces

• 論文地址：https://arxiv.org/ftp/arxiv/papers/2312/2312.00752...
• 項目地址：https://github.com/state-spaces/mamba
• 機器之心報道：五倍吞吐量，性能全面包圍Transformer：新架構Mamba引爆AI圈

圍繞 Mamba，已經有一些語言模型發布，包括 mamba-130m, mamba-370m, mamba-790m, mamba-1.4b, mamba-2.8b。

HuggingFace 地址：https://huggingface.co/state-spaces

也有人做出 Mamba-Chat：

Github 地址：https://github.com/havenhq/mamba-chat

論文三：蘋果等機構的論文 Diffusion Models Without Attention

• 論文地址：https://arxiv.org/pdf/2311.18257.pdf
• 機器之心報道：丟掉注意力的擴散模型：Mamba帶火的SSM被蘋果、康奈爾盯上了

論文四：Mamba 作者 Albert Gu 的博士論文 MODELING SEQUENCES WITH STRUCTURED STATE SPACES

論文地址：https://stacks.stanford.edu/file/druid:mb976vf9362

論文五：Long Range Language Modeling via Gated State Spaces 認為 Transformer 和 SSM 完全可以互補。

論文地址：https://arxiv.org/abs/2206.13947

論文六：DeepMind 的論文 Block-State Transformer

論文地址：https://arxiv.org/pdf/2306.09539.pdf