大家好，我是前端西瓜哥。今天我們來(lái)學(xué)變換矩陣。

線性變換

矩陣乘法是來(lái)自線性代數(shù)的內(nèi)容。

首先我們有一個(gè)二維的向量 (x, y)，它在線性代數(shù)中，我們會(huì)這么表示：

向量在幾何中會(huì)用一條起始于原點(diǎn)的箭頭表示。

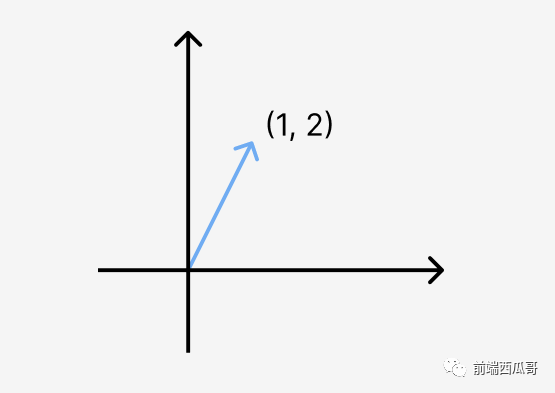
向量我們也常常看作一個(gè)點(diǎn)。因?yàn)楫?dāng)有大量向量要繪制時(shí)，箭頭就會(huì)非常的多，會(huì)讓畫(huà)面非常混亂，所以要簡(jiǎn)化為點(diǎn)。

向量加法：對(duì)應(yīng)位置進(jìn)行相加即可，在幾何中可以將多個(gè)向量頭尾相連，最終的路徑就是加法的結(jié)果：

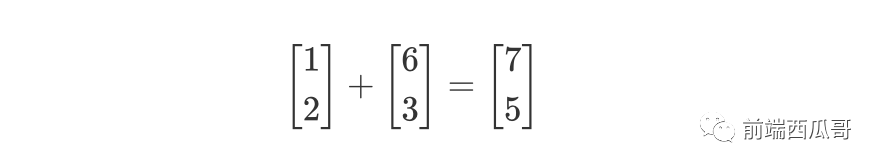
數(shù)乘：或者叫標(biāo)量乘法，指的是將向量和一個(gè)常量數(shù)字進(jìn)行相乘，也是對(duì)應(yīng)位置相乘，在幾何中表現(xiàn)為對(duì)向量縮放：

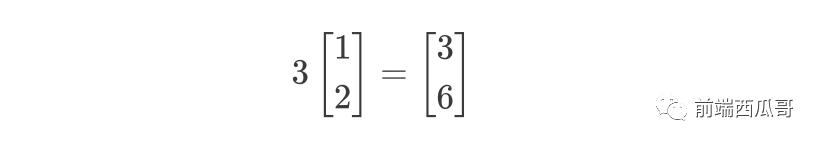
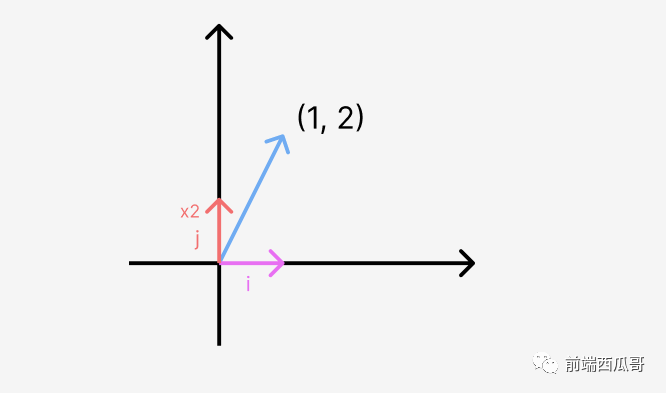
有了上面兩個(gè)概念，我們得到對(duì)于一個(gè)二維向量，它是 x 軸上和 y 軸上的單位向量（一種 基向量）進(jìn)行縮放后組合而成：

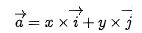
然后就是我們主角 線性變換了。

線性變換的 “變換”，指的是 “函數(shù)”，它接受一個(gè)向量，然后返回一個(gè)向量。在幾何中，它表示了一個(gè)向量是怎么從原來(lái)的指向變換（縮放旋轉(zhuǎn)等過(guò)程）成另一個(gè)指向。

線性變換的 “線性”，指的是這個(gè)變換是符合一些特性的，首先是直線變換后還是直線，然后就是原點(diǎn)保持在原來(lái)的位置。

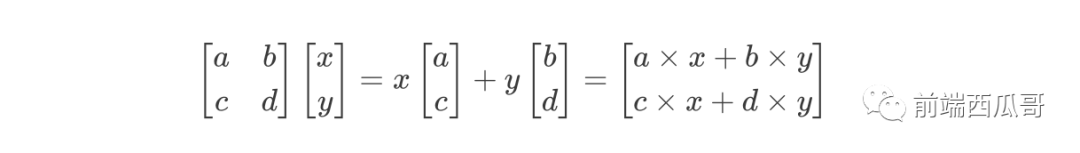
線性變換，一種理解為，矩形的每列改變了對(duì)應(yīng)基向量的值。

比如上面的公式，我們的 (x, y) 向量原來(lái)是基于 i 向量 (1, 0) 和 j 向量 (0, 1) 進(jìn)行數(shù)乘得到的。

但通過(guò)一個(gè)矩陣，我們的 i 和 j 分別變成了(a, c) 和 (b, d)，即標(biāo)準(zhǔn)換了，基于這個(gè)新標(biāo)準(zhǔn)得到的新的值就是線性變換的輸出向量。

下面我們看一些常見(jiàn)的變換矩陣。

縮放

縮放，就是將一個(gè)向量（或者點(diǎn)）的 x 和 y 各自進(jìn)行指定比例的縮放。

假設(shè) x 方向縮放比例為 sx，y 方向縮放比例為 sy。簡(jiǎn)單的算法就是：

x2 = x * sx;
y2 = y * sy;

二維 2x2 縮放矩陣為：

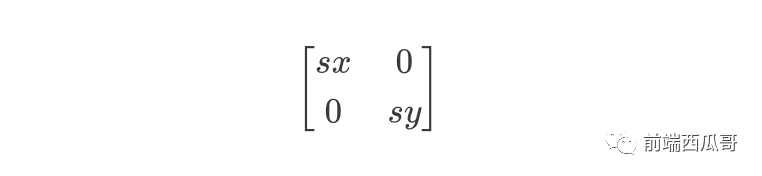
二維矩陣運(yùn)算過(guò)程為：

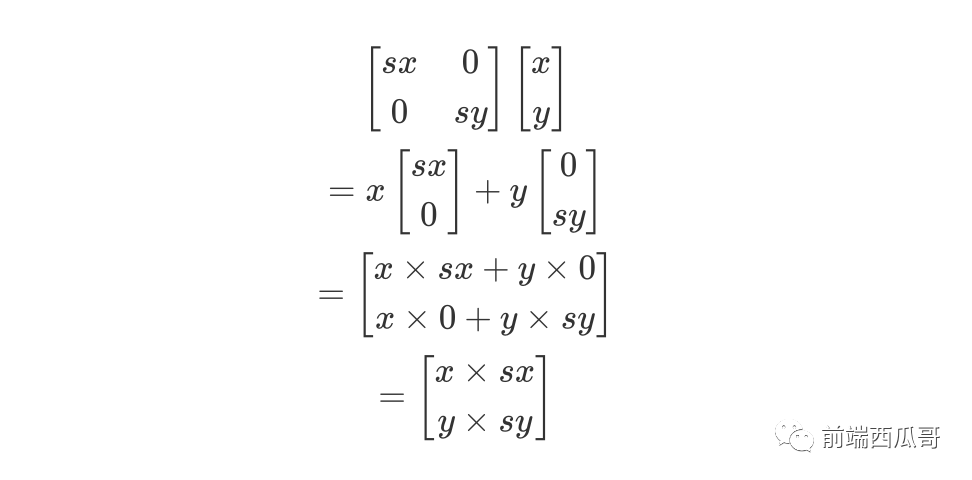
實(shí)際上我們會(huì)使用三維縮放矩陣，原因會(huì)在下面平移中講解。

三維縮放矩陣為：

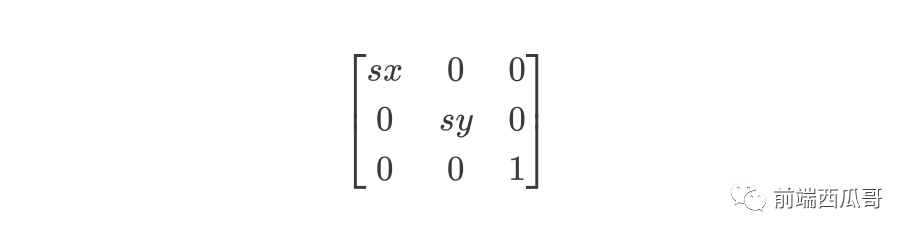
下邊和右邊各加上 0 0 1 即可。

平移

平移，就是將一個(gè)向量（或者點(diǎn)）的 x 和 y 各自移動(dòng)一段距離。

假設(shè) x 方向移動(dòng) dx 距離，y 方向移動(dòng) dy 距離。

直接用幾何的描述：

x2 = x + dx;
y2 = y + dy;

我們無(wú)法用一個(gè)二維矩陣來(lái)表示平移變換，為此我們需要升維，升到三維，通過(guò)額外的一個(gè) z 軸的基向量的斜切來(lái)模擬二維中的平移。

輸入向量也需要升維，加多一個(gè)值為 1 的第三維度：

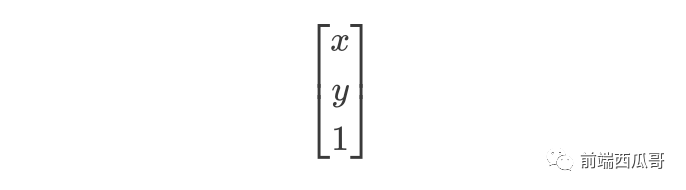
三維平移矩陣為：

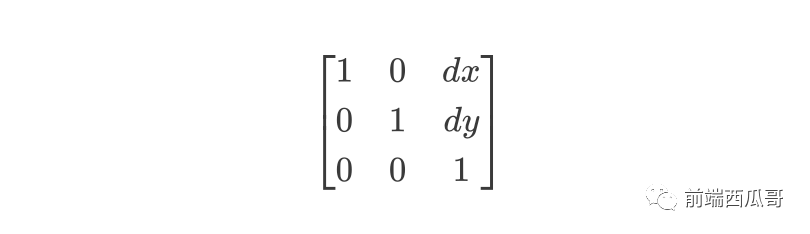
運(yùn)算過(guò)程：

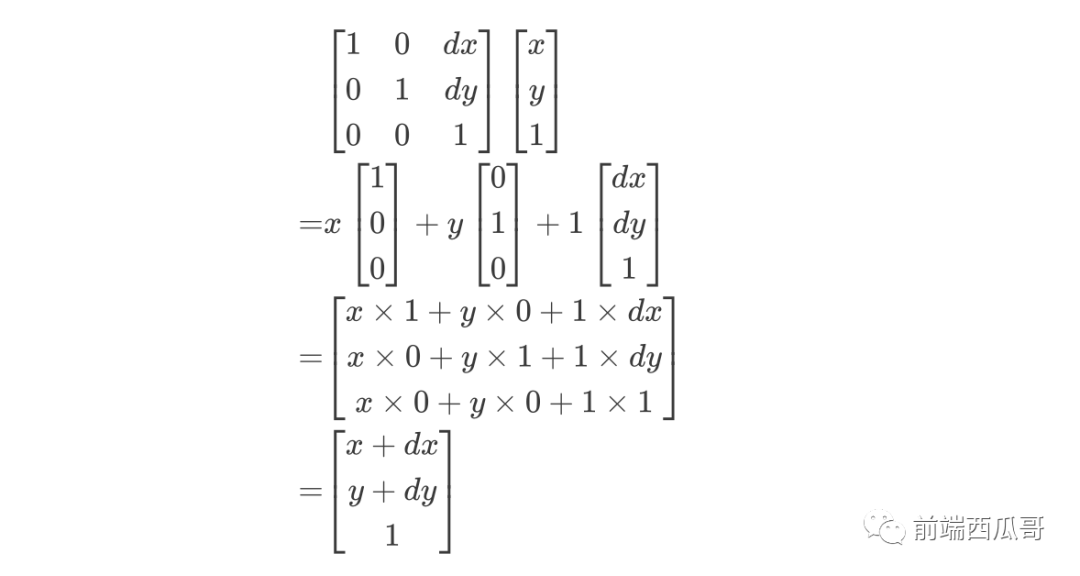
為了減少計(jì)算量，我們會(huì)使用 復(fù)合矩陣，就是將多個(gè)變換矩陣通過(guò)結(jié)合律計(jì)算出來(lái)的矩陣。

它是多種矩陣的組合體，但相比對(duì)一個(gè)向量一個(gè)個(gè)進(jìn)行矩陣乘法，符合矩陣能一次計(jì)算出來(lái)。因?yàn)槠揭频奶厥庑裕晕覀兺ǔ２粫?huì)使用 2x2 矩陣來(lái)表示一個(gè)變換矩陣，而是用 3x3 矩陣，來(lái)和平移矩陣做兼容。

旋轉(zhuǎn)

點(diǎn)沿原點(diǎn)逆時(shí)針旋轉(zhuǎn)指定角度，得到新的坐標(biāo)點(diǎn)，有以下公式：

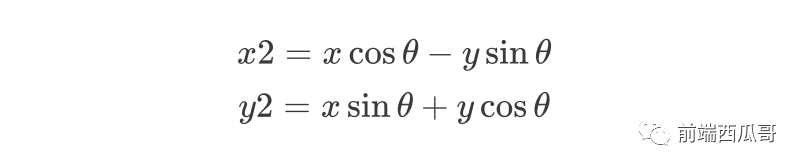
三維旋轉(zhuǎn)矩陣：

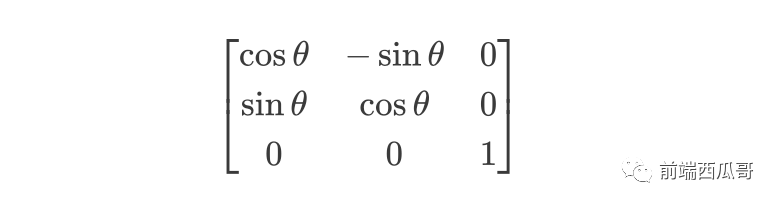
逆時(shí)針旋轉(zhuǎn) 90度，可以看作是給基變量做旋轉(zhuǎn)：

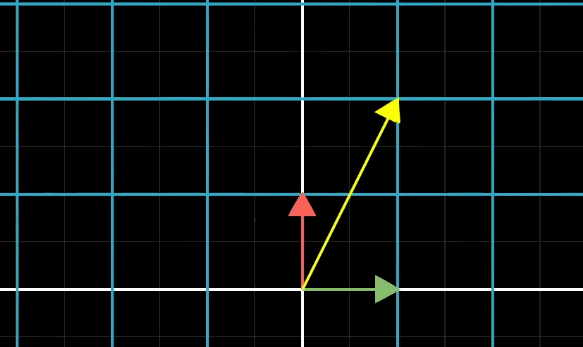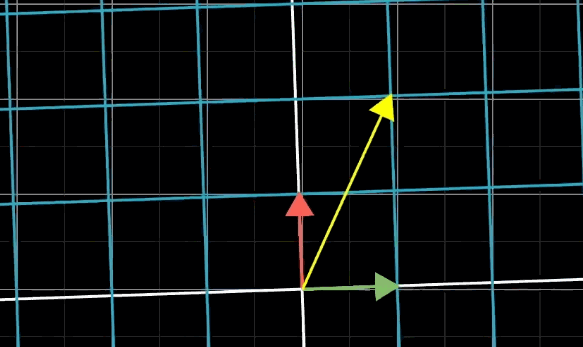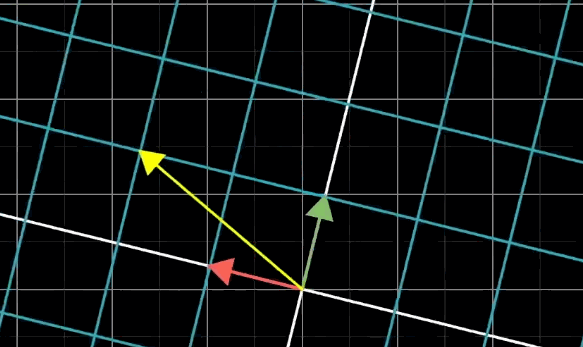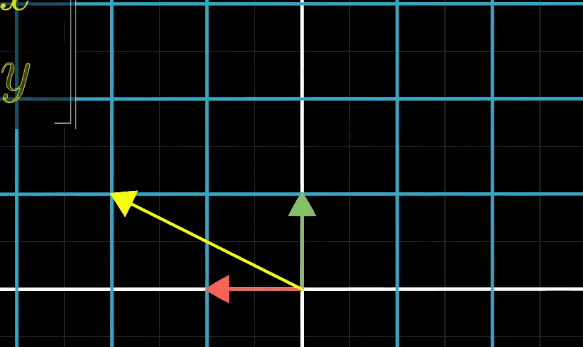
斜切

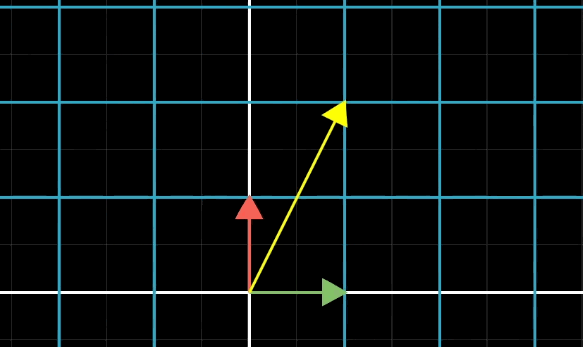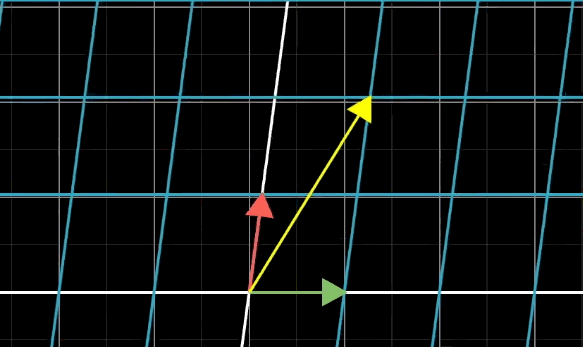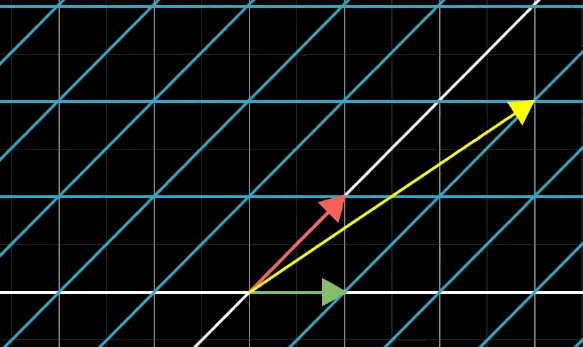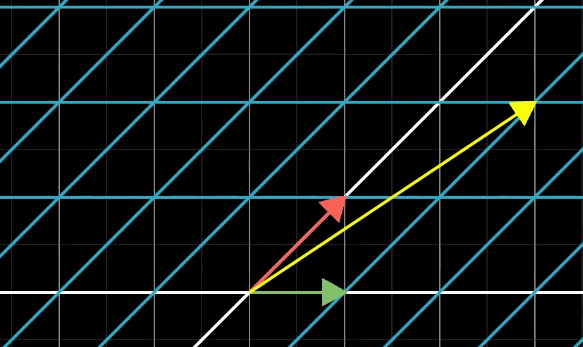
斜切，其實(shí)就是固定一個(gè)基向量不變，改變另一條基向量。斜切是有方向的。

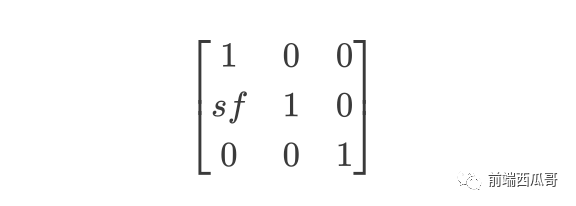
水平斜切：

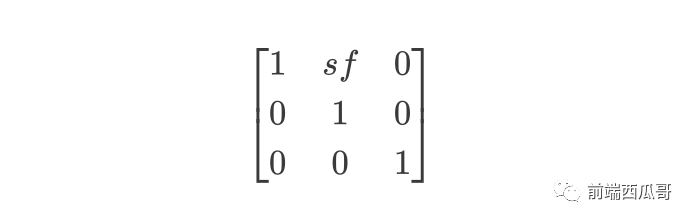
或垂直斜切：

水平斜切動(dòng)圖：

代碼實(shí)現(xiàn)

interface IVector {
  x: number;
  y: number;
}

/**
 * a c e
 * b d f
 * 0 0 1
 */
type ITransfrom = [
  a: number,
  b: number,
  c: number,
  d: number,
  e: number,
  f: number
];

/**
 * 變換矩陣
 */
export function transform(
  { x, y }: IVector,
  [a, b, c, d, e, f]: ITransfrom
): IVector {
  return {
    x: x * a + y * c + e,
    y: x * b + y * d + f,
  };
}

通常我們會(huì)用升維的 3x3 矩陣，來(lái)表示一個(gè)變換矩形，因?yàn)樽詈笠恍杏肋h(yuǎn)都是 [0, 0, 1]，所以我們的函數(shù)只需要傳矩陣的前兩行，共 6 個(gè)值。比如 Canvas 的 ctx.transform 也是只接受 6 個(gè)值。

結(jié)尾

本文簡(jiǎn)單講了一下變換矩陣。