超越SOTA 3.27%,上交大等提出自適應本地聚合新方法
本文介紹的是一篇收錄于 AAAI 2023 的論文,論文由位于上海交通大學的上海市可擴展計算與系統重點實驗室、貝爾法斯特女王大學的華揚老師和路易斯安那州立大學的王灝老師共同完成。

- 論文鏈接:??https://arxiv.org/abs/2212.01197?
- 代碼鏈接(包含ALA模塊的使用說明):??https://github.com/TsingZ0/FedALA?
該論文提出了一種用于聯邦學習的自適應本地聚合方法,通過從全局模型中自動捕獲客戶機所需信息的方式來應對聯邦學習中的統計異質性問題。作者對比了 11 個 SOTA 模型,并取得了超越最優方法 3.27% 的優異表現。作者將其中的自適應本地聚合模塊應用到其他聯邦學習方法上取得了最多 24.19% 的提升。
1 介紹
聯邦學習(FL)通過將用戶隱私數據保留在本地而不進行傳播的方式,幫助人們在保護隱私的情況下,充分發掘用戶數據中蘊含的價值。但由于客戶機之間數據不可見,數據的統計異質性(數據非獨立同分布(non-IID)和數據量不平衡現象)便成了 FL 的巨大挑戰之一。數據的統計異質性使得傳統聯邦學習方法(如 FedAvg 等)很難通過 FL 過程訓練得到適用于每個客戶機的單一全局模型。
近年來,個性化聯邦學習(pFL)方法因其應對數據統計異質性的能力受到了越來越多的關注。與尋求高質量全局模型的傳統 FL 不同,pFL 方法的目標是借助聯邦學習的協同計算能力為每個客戶機訓練適用于自身的個性化模型。現有的在服務器上聚合模型的 pFL 研究可以分為以下三類:
(1) 學習單個全局模型并對其進行微調的方法,包括 Per-FedAvg 和 FedRep;
(2) 學習額外個性化模型的方法,包括 pFedMe 和 Ditto;
(3) 通過個性化聚合(或本地聚合)學習本地模型的方法,包括 FedAMP、FedPHP、FedFomo、APPLE 和 PartialFed。
類別(1)和(2)中的 pFL 方法將全局模型中的所有信息用于本地初始化(指在每次迭代的局部訓練之前初始化局部模型)。然而,在全局模型中,只有提高本地模型質量的信息(符合本地訓練目標的客戶機所需信息)才對客戶機有益。全局模型的泛化能力較差是因為其中同時存在對于單一客戶機來說需要和不需要的信息。因此,研究者們提出類別(3)中的 pFL 方法,通過個性化聚合捕獲全局模型中每個客戶機所需的信息。但是,類別(3)中的 pFL 方法依舊存在(a)沒有考慮客戶機本地訓練目標(如 FedAMP 和 FedPHP)、(b)計算代價和通訊代價較高(如 FedFomo 和 APPLE)、(c)隱私泄露(如 FedFomo 和 APPLE)和(d)個性化聚合與本地訓練目標不匹配(如 PartialFed)等問題。此外,由于這些方法對 FL 過程做了大量修改,它們使用的個性化聚合方法并不能被直接用于大多數現有 FL 方法。
為了從全局模型中精確地捕獲客戶機所需信息,且相比于 FedAvg 不增加每一輪迭代中的通訊代價,作者提出了一種用于聯邦學習的自適應本地聚合方法(FedALA)。如圖 1 所示,FedALA 在每次本地訓練之前,通過自適應本地聚合(ALA)模塊將全局模型與本地模型進行聚合的方式,捕獲全局模型中的所需信息。由于 FedALA 相比于 FedAvg 僅使用 ALA 修改了每一輪迭代中的本地模型初始化過程,而沒有改動其他 FL 過程,因此 ALA 可被直接應用于大多數現有的其他 FL 方法,以提升它們的個性化表現。
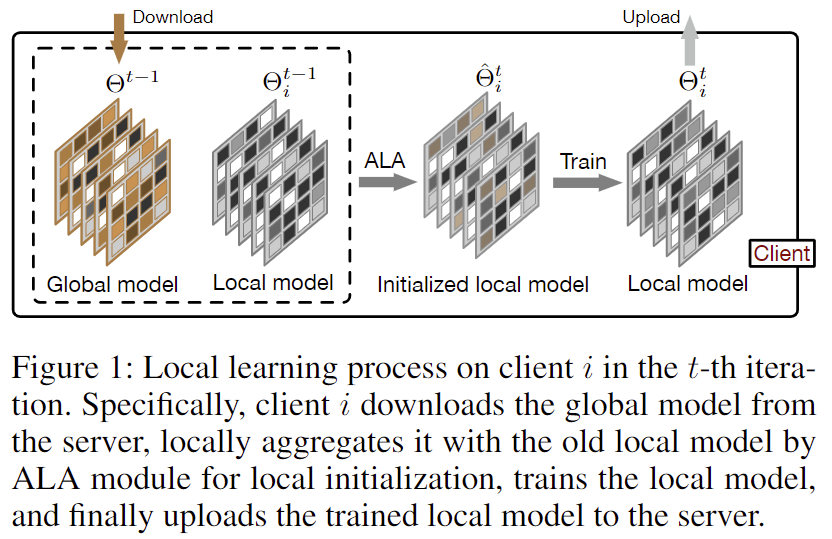
圖 1:在第次迭代中客戶機上的本地學習過程
2 方法
2.1 自適應本地聚合(ALA)?
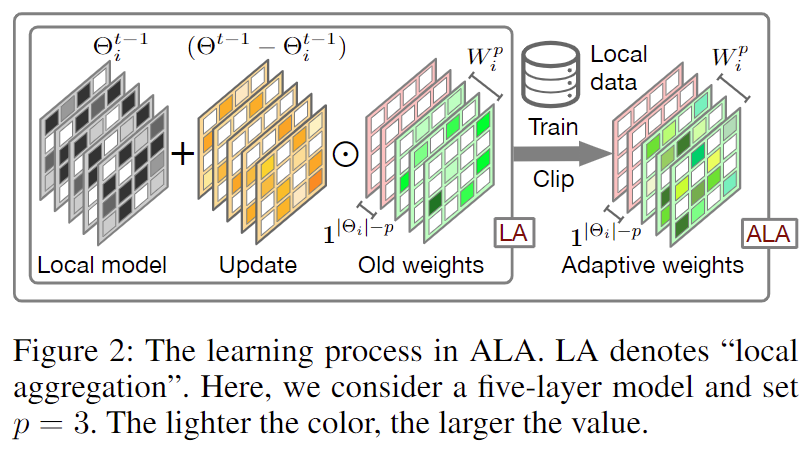
圖 2:自適應本地聚合(ALA)過程
自適應本地聚合(ALA)過程如圖 2 所示。相比于傳統聯邦學習中直接將下載的全局模型覆蓋本地模型得到本地初始化模型的方式(即),FedALA 通過為每個參數學習本地聚合權重,進行自適應本地聚合。
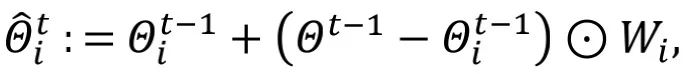
其中,作者把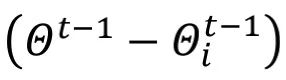 這一項稱之為“更新”。此外,作者通過逐元素權重剪枝方法
這一項稱之為“更新”。此外,作者通過逐元素權重剪枝方法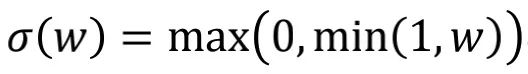 實現正則化并將
實現正則化并將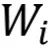 中的值限制在 [0,1] 中。
中的值限制在 [0,1] 中。
因為深度神經網絡(DNN)的較低層網絡相比于較高層傾向于學習相對更通用的信息,而通用信息是各個本地模型所需信息,所以全局模型中較低層網絡中的大部分信息與本地模型中較低層網絡所需信息一致。為了降低學習本地聚合權重所需的計算代價,作者引入一個超參數 p 來控制 ALA 的作用范圍,使得全局模型中較低層網絡參數直接覆蓋本地模型中的較低層網絡,而只在較高層啟用 ALA。
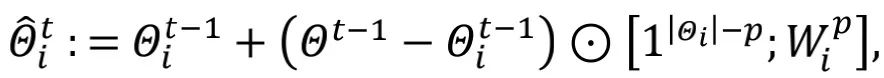
其中,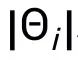 表示
表示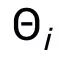 中的神經網絡層數(或神經網絡塊數),
中的神經網絡層數(或神經網絡塊數),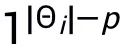 與
與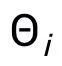 中的低層網絡形狀一致,
中的低層網絡形狀一致,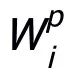 則與
則與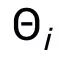 中剩下的 p 層高層網絡形狀一致。
中剩下的 p 層高層網絡形狀一致。
作者將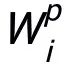 中的值全部初始化為 1,且在每一輪本地初始化過程中基于舊的
中的值全部初始化為 1,且在每一輪本地初始化過程中基于舊的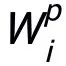 更新
更新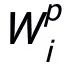 。為了進一步降低計算代價,作者采用隨機采樣 s
。為了進一步降低計算代價,作者采用隨機采樣 s
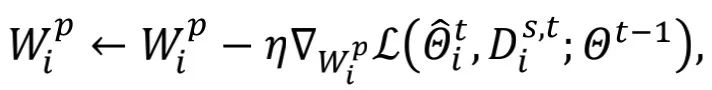
其中,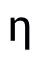 是更新
是更新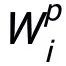 的學習率。作者在學習
的學習率。作者在學習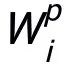 的過程中,將除
的過程中,將除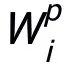 之外的其他可訓練參數凍結。
之外的其他可訓練參數凍結。
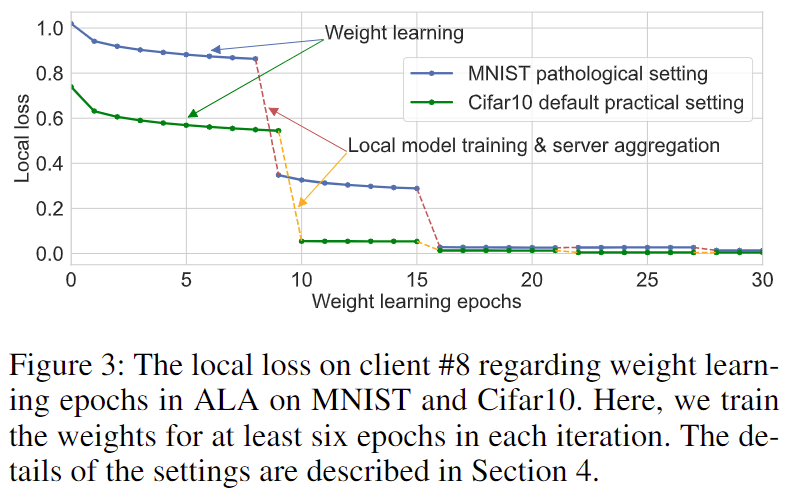
圖 3:在 MNIST 和 Cifar10 數據集上 8 號客戶機的學習曲線
通過選擇較小的 p 值,在幾乎不影響 FedALA 表現的情況下,大幅度地降低 ALA 中訓練所需的參數。此外,如圖 3,作者觀察到:一旦在第一次訓練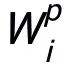 將其訓練到收斂,即使在后續迭代中訓練
將其訓練到收斂,即使在后續迭代中訓練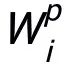 ,其對本地模型質量也沒有很大影響。也就是說,每個客戶機可以復用舊的
,其對本地模型質量也沒有很大影響。也就是說,每個客戶機可以復用舊的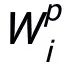 實現對其所需信息的捕獲。作者采取在后續迭代中微調
實現對其所需信息的捕獲。作者采取在后續迭代中微調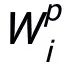 的方式,降低計算代價。
的方式,降低計算代價。
2.2 ALA 分析?
在不影響分析的情況下,為了簡便起見,作者忽略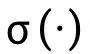 并設
并設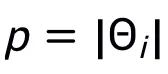 。根據上述公式可以得到
。根據上述公式可以得到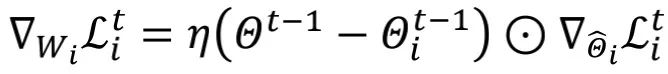 ,其中
,其中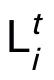 代表
代表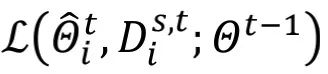 。作者可以把在 ALA 中更新
。作者可以把在 ALA 中更新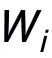 看成更新
看成更新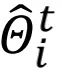 。
。
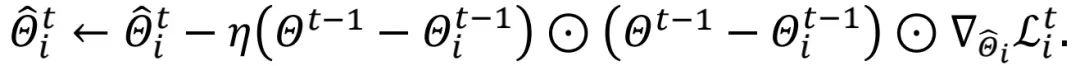
梯度項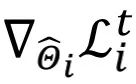 在每一輪中都做了逐元素地縮放。不同于本地模型訓練(或 fine-tuning)方法,上述對
在每一輪中都做了逐元素地縮放。不同于本地模型訓練(或 fine-tuning)方法,上述對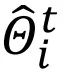 的更新過程能夠感知到全局模型中的通用信息。在不同的迭代輪數之間,動態變化的
的更新過程能夠感知到全局模型中的通用信息。在不同的迭代輪數之間,動態變化的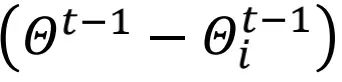 為 ALA 模塊引入了動態信息,使其 FedALA 容易適應復雜的環境。
為 ALA 模塊引入了動態信息,使其 FedALA 容易適應復雜的環境。
3 實驗
作者在實際(practical)數據異質環境下的 Tiny-ImageNet 數據集上用 ResNet-18 進行了對超參數 s 和 p 的對 FedALA 影響的研究,如表 1 所示。對于 s 來說,采用越多的隨機采樣的本地訓練數據用于 ALA 模塊學習可以使個性化模型表現更好,但也同時增加了計算代價。在使用 ALA 的過程中,可以根據每個客戶機的計算能力調整 s 的大小。從表中可以得知,即使使用極小的 s(如 s=5),FedALA 依舊具有杰出的表現。對于 p 來說,不同的 p 值對個性化模型的表現幾乎沒有影響,在計算代價方面卻有著巨大的差別。這一現象也從一個側面展示了 FedRep 等方法,將模型分割后保留靠近輸出的神經網絡層在客戶機不上傳的做法的有效性。使用 ALA 時,我們可以采用較小且合適的 p 值,在保證個性化模型表現能力的情況下,進一步降低計算代價。

表 1:關于超參數和對 FedALA 影響的研究
作者在病態(pathological)數據異質環境和實際(practical)數據異質環境下,將 FedALA 與 11 個 SOTA 方法進行了對比和詳細分析。如表 2 所示,數據顯示 FedALA 在這些情況下的表現都超越了這 11 個 SOTA 方法,其中 “TINY” 表示在 Tiny-ImageNet 上使用 4-layer CNN。例如,FedALA 在 TINY 情況下比最優基線(baseline)高了 3.27%。
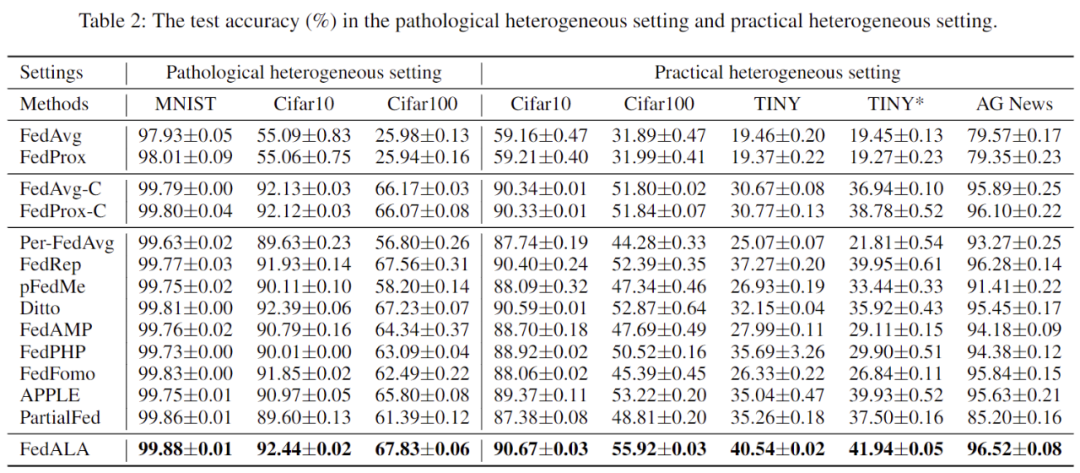
表 2:病態和實際數據異質環境下的實驗結果
此外,作者也在不同異質性環境和客戶機總量情況下評估了 FedALA 的表現。如表 3 所示,FedALA 在這些情況下依舊保持著優異的表現。
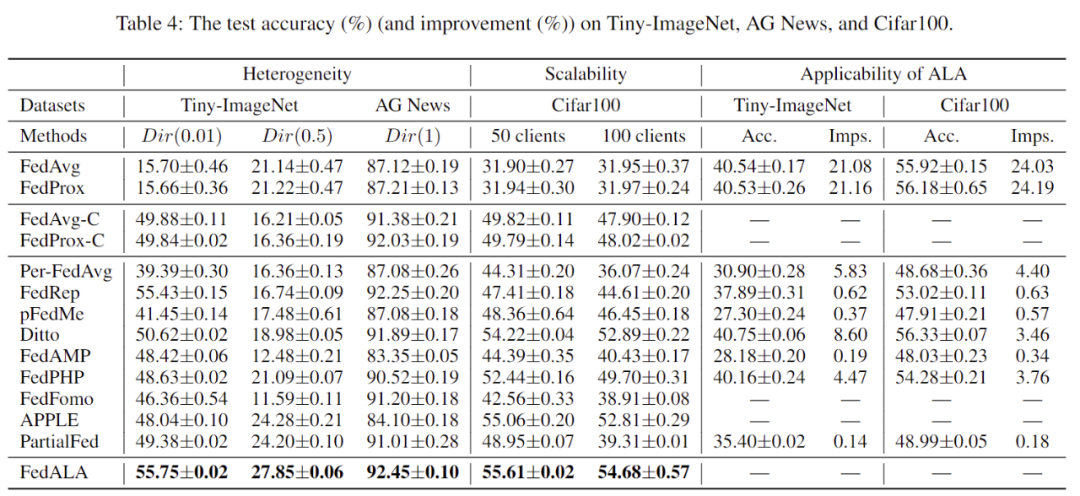
表 3:其他實驗結果
根據表 3 的實驗結果,將 ALA 模塊應用于其他方法可以獲得最多 24.19% 的提升。
最后,作者還在 MNIST 上可視化了 ALA 模塊的加入對原本 FL 過程中模型訓練的影響,如圖 4 所示。不激活 ALA 時,模型訓練軌跡與使用 FedAvg 一致。一旦 ALA 被激活,模型便可以通過全局模型中捕獲的其訓練所需信息徑直朝著最優目標優化。
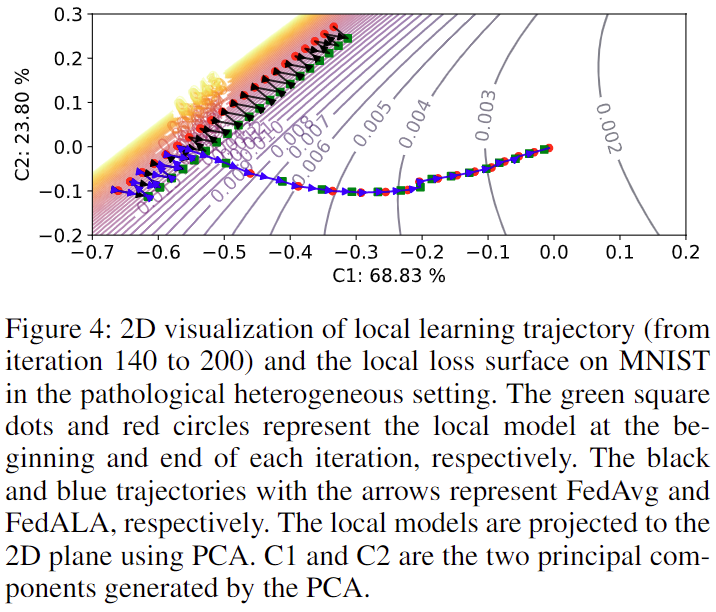
圖 4:4 號客戶機上模型訓練軌跡的可視化圖





































