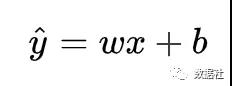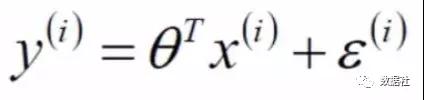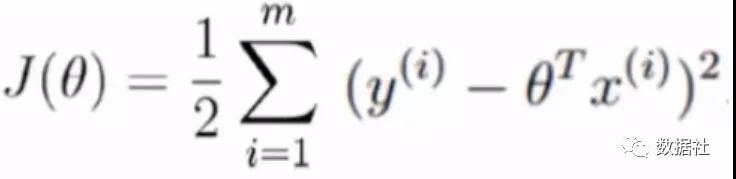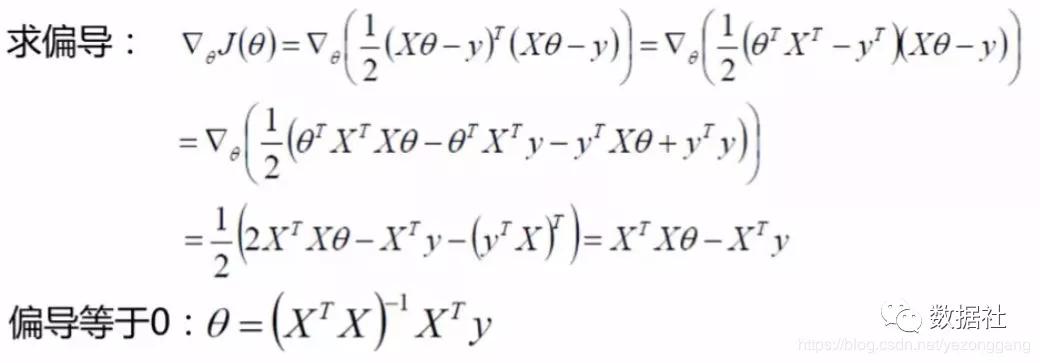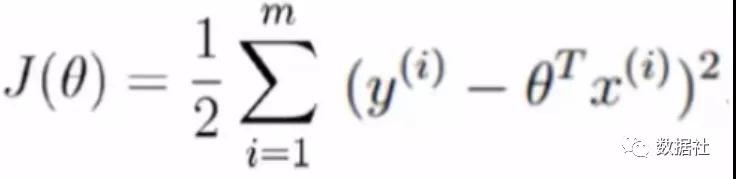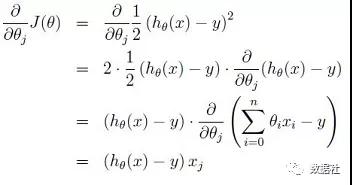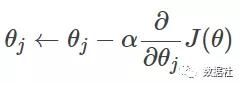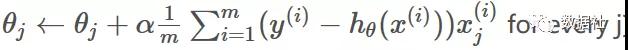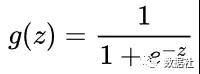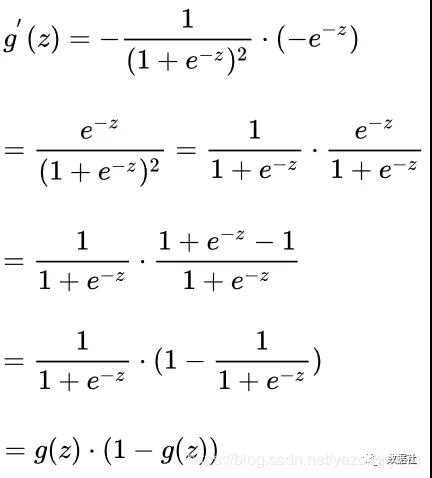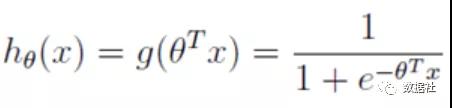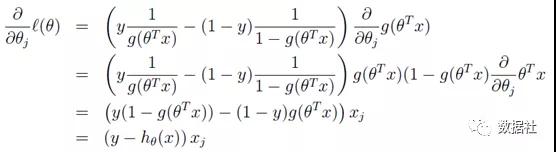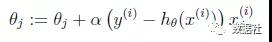數據挖掘從入門到放棄之一線性回歸和邏輯回歸
“ 數據挖掘算法基于線性代數、概率論、信息論推導,深入進去還是很有意思的,能夠理解數學家、統計學家、計算機學家的智慧,這個專欄從比較簡單的常用算法入手,后續研究基于TensorFlow的高級算法,最好能夠參與到人臉識別和NLP的實際項目中,做出來一定的效果。”
一、理解線性回歸模型
首先講回歸模型,回歸模型研究的是因變量(目標)和自變量(預測器)之間的關系,因變量可以是連續也可以離散,如果是離散的就是分類問題。思考房價預測模型,我們可以根據房子的大小、戶型、位置、南北通透等自變量預測出房子的售價,這是最簡單的回歸模型,在初中里面回歸表達式一般這樣寫,其中x是自變量,y是因變量,w是特征矩陣,b是偏置。
在機器學習推導里面引入線性代數的思想,將假設我們用一個表達式來描述放假預測模型,x代表一個房子的特征集,它是一個n×1的列向量,總共有m個特征集,θ是一個n×1的列向量,是我們想要求得未知數。
我們采用誤差最小的策略,比如有預測表達式:y工資=Θ1*學歷+Θ2*工作經驗+Θ3*技術能力+.......+Θn*x+基本工資,預測的y值和實際值y_存有差距,策略函數就是使得m個特征集的(真實值y-預測值)的平方和最小。(差值可能是負數,所以采用平方和);
按照對于正規方程的求法,我們對θ 求偏導:
也就是,給定特征矩陣X和因變量y,即可以求使誤差率最小的θ值,滿足后續的回歸模型。了解線性代數的童靴可以看出來問題,在θ的表達式中有求逆運算,需要保證矩陣可逆,這一般是無法保證的,這樣就會造成θ無解,策略失效;
二、計算機的做法:梯度下降
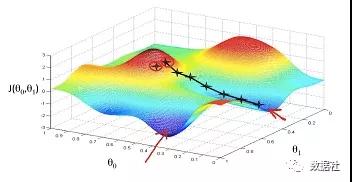
常規的方程需要大量的矩陣運算,尤其是矩陣的逆運算,在矩陣很大的情況下,會大大增加計算復雜性。,且正規方程法對矩陣求偏導有一定的局限性(無法保證矩陣可逆),下面介紹梯度下降法,也就是計算機的解決方法,每次走一小步,保證這一小步是最有效的一步,可以想象自己正在下山,你不知道目的地(全局最小值)在哪,但是你能夠保證自己每次走的都是最陡峭的一步;
我們的策略仍然保持不變,就是使得m個特征集的(真實值y-預測值)的平方和最小:
梯度下降法實現:賦予初始θ 值,并根據公式逐步更新θ 使得J(θ) 不斷減少,最終至收斂,對應的參數θ 即為解。為了推導方便,首先研究只有一個訓練樣本時,如何計算推導公式。
θ 的每個分量更新公式為:
推廣到m個訓練數據,參數更新公式為:
三、邏輯回歸模型
邏輯回歸與線性回歸同屬廣義線性模型,邏輯回歸是以線性回歸為理論支持,是一個二分類模型,也可以推廣多到分類問題,通過Sigmoid函數引入了非線性因素,因此可以輕松處理0/1分類問題,首先介紹一下Sigmoid函數:
sigmoid函數圖像是一個S曲線,取值在[0, 1]之間,在遠離0的地方函數的值會很快接近0或者1,sigmoid函數的求導特性是:
邏輯回歸的預測函數是下圖,只是在特征到結果的映射中加入了一層函數映射,先把特征線性求和,然后使用函數g(z)將最為假設函數來預測。g(z)可以將連續值映射到0到1之間:
通過求似然函數,兩邊取log后,對θ求偏導:
這樣我們就得到了梯度上升每次迭代的更新方向,那么θ的迭代表達式為:
發現同線性回歸模型是同一個表達式,這并不僅僅是巧合,兩者存在深層的聯系;
四、回歸模型使用
數據是2014年5月至2015年5月美國King County的房屋銷售價格以及房屋的基本信息。數據分為訓練數據和測試數據,分別保存在kc_train.csv和kc_test.csv兩個文件中,其中訓練數據主要包括10000條記錄,14個字段:銷售日期,銷售價格,臥室數,浴室數,房屋面積,停車面積,樓層數,房屋評分,建筑面積,地下室面積,建筑年份,修復年份,緯度,經度。
數據集地址:https://github.com/yezonggang/house_price,按照流程完成模型建立:
- import pandas as pd
- from pandas import DataFrame
- import numpy as np
- import matplotlib.pyplot as plt
- %matplotlib inline
- import seaborn as sns
- from sklearn.linear_model import LogisticRegression
- from sklearn.ensemble import RandomForestClassifier
- from sklearn.linear_model import LinearRegression
- # 數據讀取
- baseUrl="C:\\Users\\71781\\Desktop\\2020\\ML-20200422\\houre_price\\"
- house_df=pd.read_csv(baseUrl+'train.csv' )
- test_df=pd.read_csv(baseUrl+'test.csv')
- house_df.head()
- # 刪除無關變量
- house_df=house_df.drop(['saleTime','year','repairYear','latitude','longitude','buildingSize'],axis=1)
- test_df=test_df.drop(['saleTime','year','repairYear','latitude','longitude','buildingSize'],axis=1)
- # 模型建立
- X_price=house_df.drop(['price'],axis=1)
- # X_price.head()
- Y_price=house_df['price']
- Y_price.head()
- LR_reg=LinearRegression()
- LR_reg.fit(X_price, Y_price)
- Y_pred = LR_reg.predict(test_df)
- LR_reg.score(X_price, Y_price)
- # 可以選擇進行特征縮放
- #new_house=house_df.drop(['price'],axis=1)
- #from sklearn.preprocessing import MinMaxScaler
- #minmax_scaler=MinMaxScaler().fit(new_house) #進行內部擬合,內部參數會發生變化
- #scaler_housing=pd.DataFrame(minmax_scaler.transform(new_house),columns=new_house.columns)
- #mm=MinMaxScaler()
- #mm.fit(test_df)
- #scaler_t=mm.transform(test_df)
- #scaler_t=pd.DataFrame(scaler_t,columns=test_df.columns)薦
本文轉載自微信公眾號「數據社」,可以通過以下二維碼關注。轉載本文請聯系數據社公眾號。