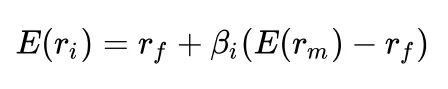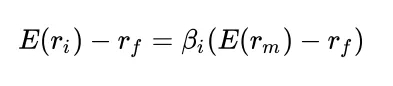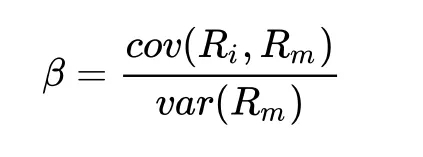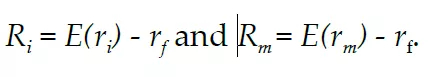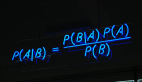用 Python 實現資本資產定價模型
Python中文社區(ID:python-china)
在本文中,我們將學習如何計算資本資產定價模型 (CAPM) 并獲得貝塔系數。資本資產定價模型(Capital Asset Pricing Model 簡稱CAPM)是由美國學者于1964年在資產組合理論和資本市場理論的基礎上發展起來的,主要研究證券市場中資產的預期收益率與風險資產之間的關系,以及均衡價格是如何形成的,是現代金融市場價格理論的支柱,廣泛應用于投資決策和公司理財領域。CAPM 被認為是一個單因子模型,在其之上可以建立更復雜的因子模型。(掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。)
CAPM 由以下等式表示:
這里,E(ri) 表示資產 i 的預期收益,rf是無風險利率(例如政府債券),E(rm) 是市場的預期收益,β 是貝塔系數。β 可以解釋為資產收益的敏感度水平,相對于一般市場水平。β 的一些情況包括:
- β <= -1:資產向與市場基準相反的方向移動,并且大于基準的負值。
- -1 < β < 0:資產向與市場基準相反的方向移動
- β = 0:資產的價格變動與市場基準一致。
- 0 < β < 1:資產與市場同向運動,但金額較小。一個例子是一家公司的股票價格容易受到日常市場波動的影響。
- β = 1:資產和市場正朝著同一方向移動相同數量。
- β > 1:資產與市場同向運動,但金額更大。一個例子是一家公司的股票非常容易受到每日市場新聞的影響。
CAPM 也可以表示為:
這里,等式的左邊可以解釋為風險溢價,而右側包含市場溢價。相同的等式可以改寫為:
其中:
在這個例子中,我們以亞馬遜股票為例并假設標普 500 指數代表市場。我們使用 5 年(2014-2018 年)的月度數據來估計 β。在當前,無風險利率如此之低,為了簡單起見,我們假設它等于零。
執行以下步驟以在 Python 中實現 CAPM:
1、導入第三方庫:
- import pandas as pd
- import yfinance as yf
- import statsmodels.api as sm
2、指定風險資產和時間范圍:
- RISKY_ASSET = 'AMZN'
- MARKET_BENCHMARK = '^GSPC'
- START_DATE = '2014-01-01'
- END_DATE = '2018-12-31'
3、從雅虎財經下載必要的數據:
- df = yf.download([RISKY_ASSET, MARKET_BENCHMARK],
- start=START_DATE,
- end=END_DATE,
- adjusted=True,
- progress=False)
4、重新采樣到每月數據并計算簡單的回報:
- X = df['Adj Close'].rename(columns={RISKY_ASSET: 'asset',
- MARKET_BENCHMARK: 'market'}) \
- .resample('M') \
- .last() \
- .pct_change() \
- .dropna()
5、使用協方差方法計算 β 值:
- covariance = X.cov().iloc[0,1]
- benchmark_variance = X.market.var()
- beta = covariance / benchmark_variance
代碼的結果是 β = 1.6709。
6、準備輸入并將 CAPM 估計為線性回歸:
- y = X.pop('asset')
- X = sm.add_constant(X)
- capm_model = sm.OLS(y, X).fit()
- print(capm_model.summary())
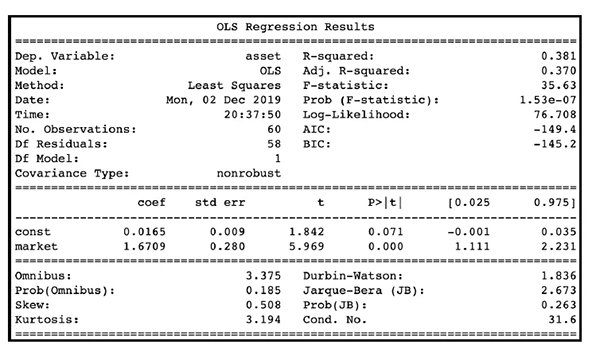
下圖顯示了估計 CAPM 模型的結果:
這些結果表明貝塔系數(此處表示為market)等于 1.67,這意味著亞馬遜股票的回報比市場波動性高 67%(由標準普爾 500 指數表示市場走勢)。截距的值比較小,在 5% 的顯著性水平上統計不顯著。
首先,我們指定了我們想要使用的資產(亞馬遜和標普 500 指數)和時間范圍。在第 3 步中,我們從雅虎財經下載了數據。然后,我們只保留了最后一個 每月可用價格并計算每月回報的百分比變化。
在第 5 步中,我們將 β 計算為風險資產與基準方差之間的協方差之比。
在第 6 步中,我們將目標(亞馬遜的股票收益)和特征(標準普爾 500 收益)使用 pandas DataFrame 的 pop 方法。之后,我們添加了常量,使用add_constant函數添加到特征(有效地添加一列)。這將截距添加到此回歸背后的想法是調查在估計模型——截距(在 CAPM 的情況下,也稱為 Jensen's alpha) 是否為零。如果它是積極的和顯著的,這意味著——假設 CAPM 模型是真——資產或投資組合會產生異常高的風險調整回報。那么有兩個可能的影響——要么市場效率低下,要么還有其他一些未被發現的模型中應包含的風險因素。這個問題被稱為聯合假設問題。
最后,我們運行 OLS 回歸并打印摘要。在這里,我們可以看到market 變量的系數(即 CAPM beta)等于計算步驟 5 中資產與市場之間的協方差。
在主要示例中,我們假設沒有無風險利率,這是一個合理的假設。但是,在某些情況下,我們可能希望考慮非零無風險利率。在本節中,我們將介紹三種可能的方法:
- 使用 Kenneth French 教授網站的數據:市場溢價 (rm-rf) 和 無風險利率(近似于 1 個月的國庫券)可以從 Kenneth French 教授的網站下載。該指數不同于標準普爾 500 指數——他的網站上有詳細說明。
- 第二種選擇是近似無風險利率,例如,13 周(3個月)國庫券(雅虎金融股票代碼:^IRX)。
請按照以下步驟了解如何下載數據并將其轉換為適當的無風險利率。
1、以天為單位定義期間的長度:
- N_DAYS = 90
2、從雅虎財經下載數據:
- df_rf = yf.download('^IRX', start=START_DATE, end=END_DATE)
3、將數據重新采樣為每月頻率(通過為每個月取最后一個值):
- rf = df_rf.resample('M').last().Close / 100
4、計算無風險收益(表示為每日值)并將值轉換為月收益:
- rf = ( 1 / (1 - rf * N_DAYS / 360) )**(1 / N_DAYS)
- rf = (rf ** 30) - 1
5、繪制計算出的無風險利率:
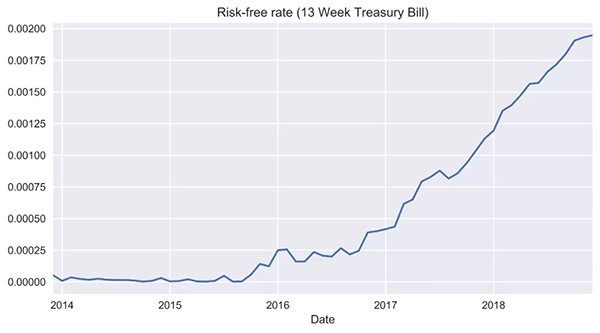
- rf.plot(title='Risk-free rate (13 Week Treasury Bill)')
下圖顯示了無風險利率隨時間的可視化:
- 最后一種方法是使用 3 個月期國庫券來估算無風險利率,可以從美聯儲經濟數據 (FRED) 數據庫下載。請按照以下步驟學習如何下載數據并將其轉換為每月無風險利率:
1、導入第三方庫:
- import pandas_datareader.data as web
2、從 FRED 數據庫下載數據:
- rf = web.DataReader('TB3MS', 'fred', start=START_DATE,
- end=END_DATE)
3、將獲得的無風險利率轉換為月值:
- rf = (1 + (rf / 100)) ** (1 / 12) - 1
4、繪制計算出的無風險利率:
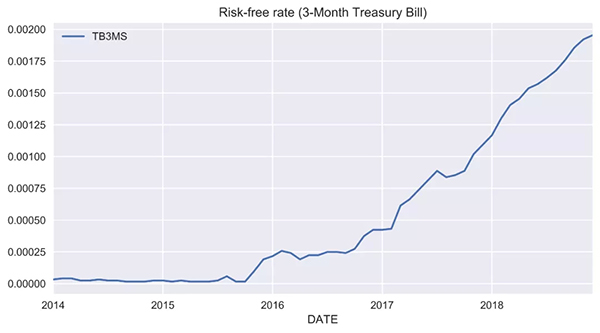
- rf.plot(title='Risk-free rate (3-Month Treasury Bill)')
我們可以通過比較兩個方法的圖來比較兩種方法的無風險利率:
我們可以看出來這些圖都非常相似。