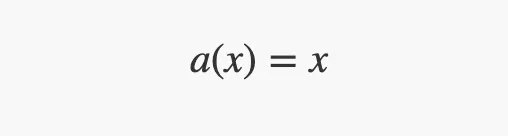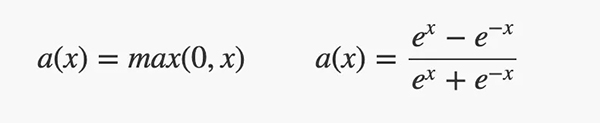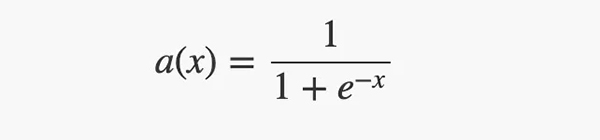Python中文社區(qū)（ID:python-china）

人工神經(jīng)網(wǎng)絡(luò) (ANN) 已成功應(yīng)用于許多需要人工監(jiān)督的日常任務(wù)，但由于其復(fù)雜性，很難理解它們的工作方式和訓(xùn)練方式。

在這篇博客中，我們深入討論了神經(jīng)網(wǎng)絡(luò)是什么、它們是如何工作的，以及如何將它們應(yīng)用于諸如尋找異常值或預(yù)測(cè)金融時(shí)間序列之類的問(wèn)題。

在這篇文章中，我嘗試直觀地展示一個(gè)簡(jiǎn)單的前饋神經(jīng)網(wǎng)絡(luò)如何在訓(xùn)練過(guò)程中將一組輸入映射到不同的空間，以便更容易理解它們。

數(shù)據(jù)

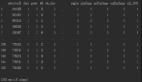
為了展示它是如何工作的，首先我創(chuàng)建了一個(gè)“ toy”數(shù)據(jù)集。它包含 400 個(gè)均勻分布在兩個(gè)類（0 和 1）中的樣本，每個(gè)樣本具有兩個(gè)維度（X0 和 X1）。

注：所有數(shù)據(jù)均來(lái)自三個(gè)隨機(jī)正態(tài)分布，均值為 [-1, 0, 1]，標(biāo)準(zhǔn)差為 [0.5, 0.5, 0.5]。

網(wǎng)絡(luò)架構(gòu)

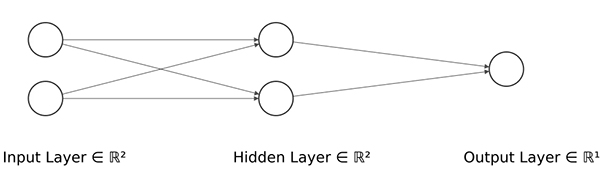
下一步是定義ANN的結(jié)構(gòu)，如下：

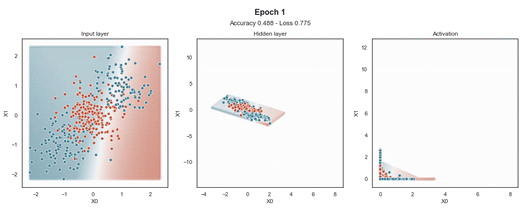
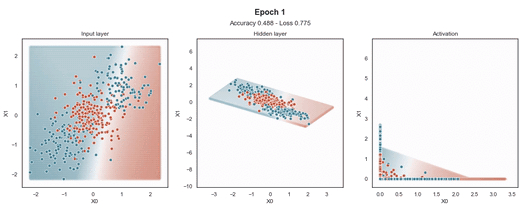
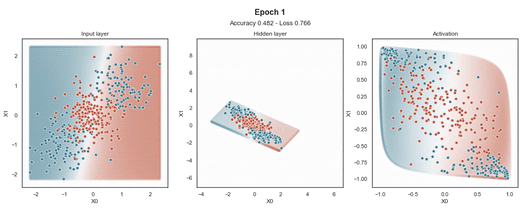
隱藏層的維度最小（2 個(gè)神經(jīng)元）以顯示網(wǎng)絡(luò)在 2D 散點(diǎn)圖中映射每個(gè)樣本的位置。

盡管前面的圖表沒(méi)有顯示，但每一層都有一個(gè)修改其輸出的激活函數(shù)。

•輸入層有一個(gè)linear激活函數(shù)來(lái)復(fù)制它的輸入值。

•隱藏層具有ReLU或tanh激活函數(shù)。

•輸出層有一個(gè)sigmoid激活函數(shù)，可以將其輸入值“縮小”到 [0, 1] 范圍內(nèi)。

訓(xùn)練

除了網(wǎng)絡(luò)的架構(gòu)之外，神經(jīng)網(wǎng)絡(luò)的另一個(gè)關(guān)鍵方面是訓(xùn)練過(guò)程。訓(xùn)練 ANN 的方法有很多種，但最常見的是反向傳播過(guò)程。

反向傳播過(guò)程首先將所有訓(xùn)練案例（或一批）前饋到網(wǎng)絡(luò)，然后優(yōu)化器根據(jù)損失函數(shù)計(jì)算“如何”更新網(wǎng)絡(luò)的權(quán)重，并根據(jù)學(xué)習(xí)率更新它們。

當(dāng)損失收斂、經(jīng)過(guò)一定數(shù)量的 epoch 或用戶停止訓(xùn)練時(shí)，訓(xùn)練過(guò)程停止。一個(gè)epoch 表示所有的數(shù)據(jù)送入網(wǎng)絡(luò)中， 完成了一次前向計(jì)算 + 反向傳播的過(guò)程。

在我們的研究案例中，該架構(gòu)使用隱藏層中的 2 個(gè)不同激活函數(shù)（ReLU 和 Tanh）和 3 個(gè)不同的學(xué)習(xí)率（0.1、0.01 和 0.001）進(jìn)行訓(xùn)練。

在輸入樣本周圍，有一個(gè)“網(wǎng)格”點(diǎn)，顯示模型為該位置的樣本提供的預(yù)測(cè)概率。這使得模型在訓(xùn)練過(guò)程中生成的邊界更加清晰。 

# figure holding the evolution  
f, axes = plt.subplots(1, 3, figsize=(18, 6), gridspec_kw={'height_ratios':[.9]})  
f.subplots_adjust(top=0.82)  
# camera to record the evolution  
camera = Camera(f)  
# number of epochs  
epochs = 20  
# iterate epoch times  
for i in range(epochs):  
    # evaluate the model (acc, loss)  
    evaluation = model.evaluate(x_train, y_train, verbose=0)  
    # generate intermediate models  
    model_hid_1 = Model(model.input, model.get_layer("hidden_1").output)  
    model_act_1 = Model(model.input, model.get_layer("activation_1").output) 
     # generate data  
    df_hid_1 = pd.DataFrame(model_hid_1.predict(x_train), columns=['X0', 'X1'])  
    df_hid_1['y'] = y_train  
    df_act_1 = pd.DataFrame(model_act_1.predict(x_train), columns=['X0', 'X1'])  
    df_act_1['y'] = y_train  
    # generate meshgrid (200 values)  
    x = np.linspace(x_train[:,0].min(), x_train[:,0].max(), 200)  
    y = np.linspace(x_train[:,1].min(), x_train[:,1].max(), 200)  
    xv, yv = np.meshgrid(x, y)  
    # generate meshgrid intenisty  
    df_mg_train = pd.DataFrame(np.stack((xv.flatten(), yv.flatten()), axis=1), columns=['X0', 'X1'])  
    df_mg_train['y'] = model.predict(df_mg_train.values)  
    df_mg_hid_1 = pd.DataFrame(model_hid_1.predict(df_mg_train.values[:,:-1]), columns=['X0', 'X1'])  
    df_mg_hid_1['y'] = model.predict(df_mg_train.values[:,:-1])  
    df_mg_act_1 = pd.DataFrame(model_act_1.predict(df_mg_train.values[:,:-1]), columns=['X0', 'X1'])  
    df_mg_act_1['y'] = model.predict(df_mg_train.values[:,:-1])  
    # show dataset        
    ax = sns.scatterplot(x='X0', y='X1', data=df_mg_train, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[0], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15) 
    ax = sns.scatterplot(x='X0', y='X1', data=df_train, hue='y', legend=None, ax=axes[0], palette=sns.diverging_palette(220, 20, n=2)) 
    ax.set_title('Input layer')  
    ax = sns.scatterplot(x='X0', y='X1', data=df_mg_hid_1, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[1], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15) 
    ax = sns.scatterplot(x='X0', y='X1', data=df_hid_1, hue='y', legend=None, ax=axes[1], palette=sns.diverging_palette(220, 20, n=2)) 
    ax.set_title('Hidden layer')  
    # show the current epoch and the metrics  
    ax.text(x=0.5, y=1.15, s='Epoch {}'.format(i+1), fontsize=16, weight='bold', ha='center', va='bottom', transform=ax.transAxes)  
    ax.text(x=0.5, y=1.08, s='Accuracy {:.3f} - Loss {:.3f}'.format(evaluation[1], evaluation[0]), fontsize=13, ha='center', va='bottom', transform=ax.transAxes)  
    ax = sns.scatterplot(x='X0', y='X1', data=df_mg_act_1, hue='y', x_jitter=True, y_jitter=True, legend=None, ax=axes[2], palette=sns.diverging_palette(220, 20, as_cmap=True), alpha=0.15) 
    ax = sns.scatterplot(x='X0', y='X1', data=df_act_1, hue='y', legend=None, ax=axes[2], palette=sns.diverging_palette(220, 20, n=2)) 
    ax.set_title('Activation')  
    # show the plot  
    plt.show()  
    # call to generate the GIF  
    camera.snap()  
    # stop execution if loss <= 0.263 (avoid looping 200 times if not needed)  
    if evaluation[0] <= 0.263:  
        break  
    # train the model 1 epoch  
    model.fit(x_train, y_train, epochs=1, verbose=0) 

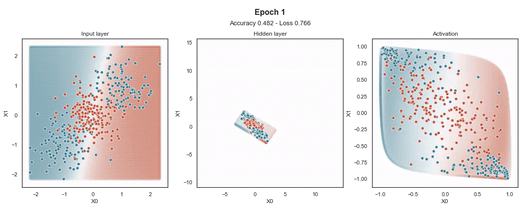
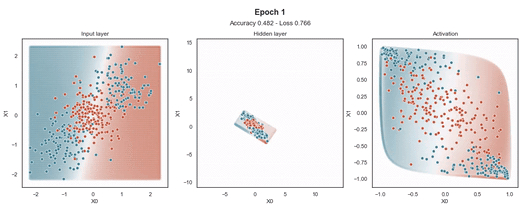
ReLU 激活

Tanh 激活

注意：使用的損失函數(shù)是二元交叉熵，因?yàn)槲覀冋谔幚矶诸悊?wèn)題，而優(yōu)化器是對(duì)原始隨機(jī)梯度下降 (SGD) 稱為 Adam 的修改。當(dāng)epoch達(dá)到 200 或損失低于 0.263 時(shí)，模型訓(xùn)練停止。