[[418609]]

蒙特卡洛方法（或蒙特卡洛實驗）是一大類計算算法，它們依賴于重復隨機采樣來獲得數值結果。基本思想是使用隨機性來解決原則上可能是確定性的問題。它們通常用于物理和數學問題，并且在難以或不可能使用其他方法時最有用。Monte Carlo 方法主要用于三個不同的問題類別：優化、數值積分和從概率分布中生成繪圖。

我們將使用蒙特卡洛模擬來觀察資產價格隨時間的潛在變化，假設它們的每日收益服從正態分布。這種類型的價格演變也稱為“隨機游走”（random walk）。

例如，如果我們想購買一只特定的股票，我們可能想嘗試展望未來并預測可以以何種概率期望得到何種回報，或者我們可能有興趣調查哪些潛在的極端結果。我們可能會經歷以及我們面臨破產風險的程度，或者另一方面，獲得超額回報的風險。

為了建立模擬，我們需要估計相關股票的預期回報水平 (mu) 和波動率 (vol)。這些數據可以從歷史價格中估計出來，最簡單的方法是假設過去的平均回報和波動率水平將持續到未來。還可以調整歷史數據以考慮投資者觀點或市場制度變化等，但是為了保持簡單并專注于代碼，我們將根據過去的價格數據設置簡單的回報和波動率水平。

現在讓我們開始編寫一些代碼并生成我們需要的初始數據作為我們蒙特卡羅模擬的輸入。出于說明目的，讓我們看看蘋果公司的股票......

首先我們必須導入必要的模塊，然后開始： 

#import necessary packages  
import numpy as np  
import math  
import matplotlib.pyplot as plt  
from scipy.stats import norm  
from pandas_datareader import data  
#download Apple price data into DataFrame  
apple = data.DataReader('AAPL', 'yahoo',start='1/1/2000')  
#calculate the compound annual growth rate (CAGR) which   
#will give us our mean return input (mu)  
days = (apple.index[-1] - apple.index[0]).days  
cagr = ((((apple['Adj Close'][-1]) / apple['Adj Close'][1])) ** (365.0/days)) - 1  
print ('CAGR =',str(round(cagr,4)*100)+"%")  
mu = cagr  
#create a series of percentage returns and calculate   
#the annual volatility of returns  
apple['Returns'] = apple['Adj Close'].pct_change()  
vol = apple['Returns'].std()*sqrt(252)  
print ("Annual Volatility =",str(round(vol,4)*100)+"%") 

結果如下： 

CAGR = 23.09%  
Annual Volatility = 42.59% 

現在我們知道我們的復合年均增長率是 23.09%，我們的波動率輸入 (vol) 是 42.59%——實際運行蒙特卡羅模擬的代碼如下： 

#Define Variables  
S = apple['Adj Close'][-1] #starting stock price (i.e. last available real stock price)  
T = 252 #Number of trading days  
mu = 0.2309 #Return  
vol = 0.4259 #Volatility  
#create list of daily returns using random normal distribution  
daily_returns=np.random.normal((mu/T),vol/math.sqrt(T),T)+1  
#set starting price and create price series generated by above random daily returns  
price_list = [S]  
for x in daily_returns:  
    price_list.append(price_list[-1]*x)  
#Generate Plots - price series and histogram of daily returns  
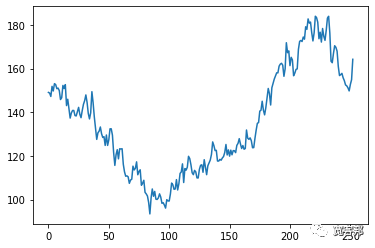
plt.plot(price_list)  
plt.show()  
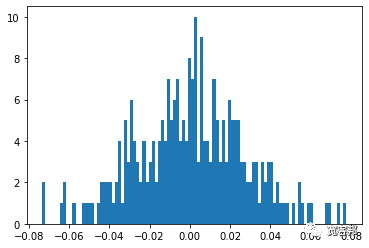
plt.hist(daily_returns-1, 100) #Note that we run the line plot and histogram separately, not simultaneously.  
plt.show() 

此代碼輸出繪圖：

上面的代碼基本上運行了一個交易年度（252 天）內潛在價格序列演變的單一模擬，基于遵循正態分布的每日收益隨機的抽取。由第一個圖表中顯示的單線系列表示。第二個圖表繪制了一年期間這些隨機每日收益的直方圖。

現在我們已經成功模擬了未來一年的每日價格數據。但實際上它并沒有讓我們深入了解股票的風險和回報特征，因為我們只有一個隨機生成的路徑。實際價格完全按照上表所述演變的可能性幾乎為零。

那么你可能會問這個模擬有什么意義呢？好吧，真正的洞察力是通過運行數千次、數萬次甚至數十萬次模擬獲得的，每次運行都會根據相同的股票特征（mu 和 vol）產生一系列不同的潛在價格演變。

我們可以非常簡單地調整上面的代碼來運行多個模擬。此代碼如下所示。在下面的代碼中，您會注意到一些事情——首先我刪除了直方圖（我們稍后會以稍微不同的方式回到這個問題），并且代碼現在在一個圖表上繪制多個價格系列以顯示信息對于每個單獨的模擬運行。 

import numpy as np  
import math  
import matplotlib.pyplot as plt  
from scipy.stats import norm  
#Define Variables  
S = apple['Adj Close'][-1] #starting stock price (i.e. last available real stock price)  
T = 252 #Number of trading days  
mu = 0.2309 #Return  
vol = 0.4259 #Volatility  
#choose number of runs to simulate - I have chosen 1000  
for i in range(1000):  
    #create list of daily returns using random normal distribution  
    daily_returns=np.random.normal(mu/T,vol/math.sqrt(T),T)+1  
    #set starting price and create price series generated by above random daily returns  
    price_list = [S]  
    for x in daily_returns:  
        price_list.append(price_list[-1]*x)  
    #plot data from each individual run which we will plot at the end 
    plt.plot(price_list)  
#show the plot of multiple price series created above  
plt.show() 

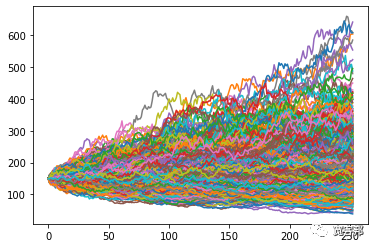
這為我們提供了以下 1000 個不同模擬價格系列的圖:

現在我們可以看到 1000 次不同模擬產生的潛在結果，考慮到每日收益序列的隨機性，所有模擬都基于相同的基本輸入。

最終價格的差價相當大，從大約 45 美元到 500 美元不等！

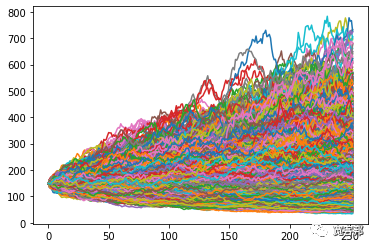
在當前的格式中，由于圖表中充滿了數據，因此很難真正清楚地看到正在發生的事情——所以這就是我們回到之前刪除的直方圖的地方，盡管這次它會向我們展示 結束模擬值的分布，而不是單個模擬的每日收益分布。這次我還模擬了 10,000 次運行，以便為我們提供更多數據。

同樣，代碼很容易調整以包含此直方圖。 

import numpy as np  
import math  
import matplotlib.pyplot as plt  
from scipy.stats import norm  
#set up empty list to hold our ending values for each simulated price series  
result = []  
#Define Variables  
S = apple['Adj Close'][-1] #starting stock price (i.e. last available real stock price)  
T = 252 #Number of trading days  
mu = 0.2309 #Return  
vol = 0.4259 #Volatility  
#choose number of runs to simulate - I have chosen 10,000  
for i in range(10000):  
    #create list of daily returns using random normal distribution  
    daily_returns=np.random.normal(mu/T,vol/math.sqrt(T),T)+1  
    #set starting price and create price series generated by above random daily returns  
    price_list = [S]  
    for x in daily_returns:  
        price_list.append(price_list[-1]*x)  
    #plot data from each individual run which we will plot at the end  
    plt.plot(price_list)  
    #append the ending value of each simulated run to the empty list we created at the beginning  
    result.append(price_list[-1])  
#show the plot of multiple price series created above  
plt.show()  
#create histogram of ending stock values for our mutliple simulations  
plt.hist(result,bins=50)  
plt.show() 

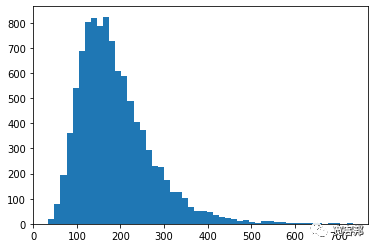
輸出如下：

我們現在可以快速計算分布的平均值以獲得我們的“預期值”： 

#use numpy mean function to calculate the mean of the result  
print(round(np.mean(result),2)) 

輸出188.41。當然，您會得到略有不同的結果，因為這些是隨機每日回報抽取的模擬。您在每次模擬中包含的路徑或運行次數越多，平均值就越傾向于我們用作“mu”輸入的平均回報。這是大數定律的結果。

我們還可以查看潛在價格分布的幾個“分位數”，以了解非常高或非常低回報的可能性。

我們可以使用 numpy 的“percentile”函數來計算 5% 和 95% 的分位數： 

print("5% quantile =",np.percentile(result,5))  
print("95% quantile =",np.percentile(result,95))  
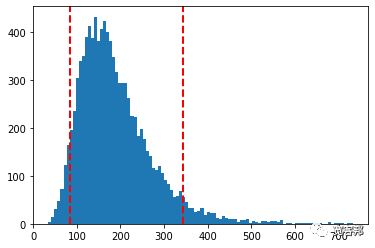
5% quantile = 85.02689052048294  
95% quantile = 344.5558966477557 

我們現在知道，股價有 5% 的可能性最終會低于 85.02 美元，有 5% 的可能性會高于 344.55 美元。

我們可以開始問自己這樣的問題：“我是否愿意冒 5% 的風險最終獲得價值低于 63.52 美元的股票，以追逐股價在 188.41 美元左右的預期回報？”

最后要做的就是在直方圖上快速繪制我們剛剛計算的兩個分位數，以給我們一個直觀的表示。掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。 

plt.hist(result,bins=100)  
plt.axvline(np.percentile(result,5), color='r', linestyle='dashed', linewidth=2)  
plt.axvline(np.percentile(result,95), color='r', linestyle='dashed', linewidth=2)  
plt.show()