Python量化投資實踐：基于蒙特卡洛模擬的投資組合風險建模與分析
作者：Michael Whittle
蒙特卡洛模擬是一種基于重復隨機抽樣獲取數(shù)值結(jié)果的計算算法。該方法的核心原理在于利用隨機性解決本質(zhì)上可能具有確定性的問題。其命名源自摩納哥的蒙特卡洛賭場，這體現(xiàn)了該方法中固有的隨機性特征。在金融與交易等多個領域，該方法被廣泛應用于不確定性場景的建模和風險影響評估。
蒙特卡洛模擬是一種基于重復隨機抽樣獲取數(shù)值結(jié)果的計算算法。該方法的核心原理在于利用隨機性解決本質(zhì)上可能具有確定性的問題。其命名源自摩納哥的蒙特卡洛賭場，這體現(xiàn)了該方法中固有的隨機性特征。在金融與交易等多個領域，該方法被廣泛應用于不確定性場景的建模和風險影響評估。
在金融應用領域，蒙特卡洛模擬主要用于股票和加密貨幣市場的分析。通過構(gòu)建資產(chǎn)價格的多種可能路徑來預測未來價格走勢。考慮到金融市場的隨機特性，該方法特別適合于評估投資過程中的固有風險和不確定性。投資者和分析師通過該方法對不同盈利可能性進行建模，通過全面了解可能結(jié)果的分布范圍及其實現(xiàn)概率，從而制定更為合理的投資決策。
在股票和加密貨幣分析中，模擬過程主要基于歷史波動率和價格趨勢對未來價格進行預測。具體實施步驟如下：
- 歷史數(shù)據(jù)分析：對歷史價格數(shù)據(jù)（OHLC：開盤價、最高價、最低價、收盤價）進行分析，確定平均收益率和波動率參數(shù)。
- 隨機樣本生成：基于歷史平均收益率和波動率，采用統(tǒng)計模型生成隨機日收益率序列。
- 價格路徑模擬：將隨機生成的收益率序列應用于當前價格，重復計算生成多條可能的未來價格路徑。
- 結(jié)果分析：對模擬生成的未來價格分布進行統(tǒng)計分析，估計不同結(jié)果的發(fā)生概率。
本文將分兩個部分詳細講解實現(xiàn)過程，以便更好地理解其核心原理和具體應用。
第一部分：數(shù)據(jù)獲取與基礎模擬
首先需要獲取歷史交易數(shù)據(jù)作為模擬基礎。本文使用EODHD APIs提供的數(shù)據(jù)服務。EODHD提供了名為"eodhd"的Python庫，可以方便地獲取所需的數(shù)據(jù)。以下示例將使用標準普爾500指數(shù)的每日交易數(shù)據(jù)進行分析。
python3 -m pip install eodhd -Uimport numpy as np
import matplotlib.pyplot as plt
from eodhd import APIClient
API_KEY = "<YOUR_KEY>"
api = APIClient(API_KEY)
df = api.get_historical_data("GSPC.INDX", "d", results=365)
print(df)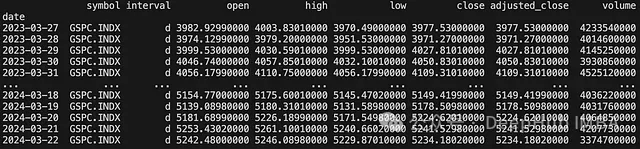
# 計算日收益率序列
daily_returns = df["adjusted_close"].pct_change().dropna()
print(daily_returns)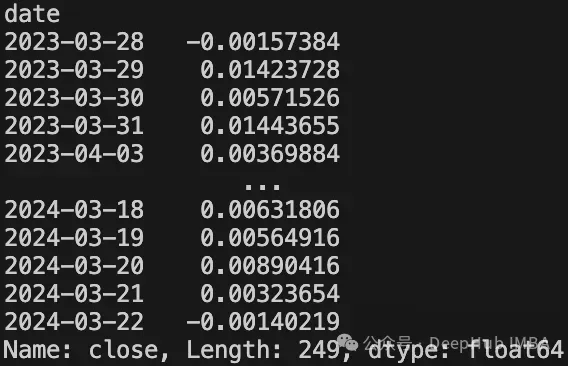
# 定義模擬參數(shù)
num_simulations = 1000 # 模擬路徑數(shù)量
forecast_days = 365 # 預測天數(shù)
# 初始化模擬數(shù)組
simulations = np.zeros((num_simulations, forecast_days))
# 生成價格路徑
last_price = df["adjusted_close"].iloc[-1]
for i in range(num_simulations):
cumulative_returns = np.random.choice(daily_returns, size=forecast_days, replace=True).cumsum()
simulations[i, :] = last_price * (1 + cumulative_returns)
print(simulations)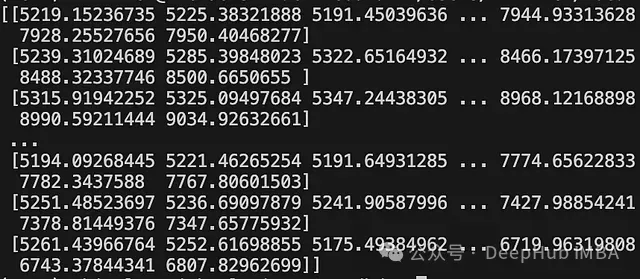
可視化模擬結(jié)果
# 繪制價格路徑
plt.figure(figsize=(10, 6))
plt.plot(simulations.T, color="blue", alpha=0.025)
plt.title("Monte Carlo Simulation of Future Prices")
plt.xlabel("Day")
plt.ylabel("Price")
plt.show()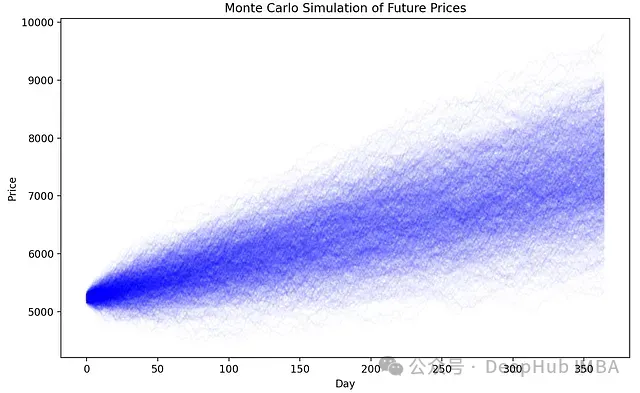
上述模擬結(jié)果展示了幾個關鍵的技術特征：
- 波動率特征捕捉：模擬通過歷史波動率數(shù)據(jù)捕捉了價格變動的可能范圍，提供了不確定性的定量表示。然而需要注意的是，該方法基于歷史波動模式的持續(xù)性假設，這在實際市場環(huán)境中可能存在偏差。
- 預測能力邊界：雖然模擬對于理解潛在結(jié)果分布具有重要價值，但其無法準確預測具體的未來價格點位。市場條件、宏觀經(jīng)濟因素以及突發(fā)事件都可能導致實際結(jié)果偏離模擬范圍。
- 情景分析框架：模擬結(jié)果的分布為投資者提供了系統(tǒng)的情景分析框架，有助于在收益潛力與損失風險之間進行量化權(quán)衡。這種方法推動了從確定性預測向概率思維的轉(zhuǎn)變。
- 模型依賴性：模擬精度在很大程度上取決于收益分布和波動率假設的合理性。不同的分布假設（如正態(tài)分布與對數(shù)正態(tài)分布）可能產(chǎn)生顯著不同的結(jié)果，這凸顯了模型選擇和參數(shù)校準的重要性。
在理解了基礎實現(xiàn)之后，我們將深入探討蒙特卡洛模擬在投資風險評估和決策制定中的實際應用。通過分析第一部分生成的未來價格分布，我們可以構(gòu)建量化的風險-收益評估框架。
投資決策框架的關鍵要素
投資目標與風險偏好量化
投資組合管理的首要步驟是明確定義投資目標并量化風險承受能力。這包括：
- 預期收益率的具體目標設定
- 風險承受能力的量化界定
- 投資期限的明確規(guī)劃
- 流動性需求的評估
這些參數(shù)受到投資期限、財務目標特征以及投資者風險偏好等因素的綜合影響。
模擬執(zhí)行的技術實現(xiàn)
利用歷史數(shù)據(jù)和統(tǒng)計模型構(gòu)建預測框架，對目標投資品種（如股票、加密貨幣等）的價格路徑進行大規(guī)模模擬。每條模擬路徑代表了基于歷史波動特征的一種可能市場情景。
模擬結(jié)果的量化分析
蒙特卡洛模擬輸出的關鍵分析指標包括：
- 概率分布特征：通過分析模擬終值的分布特征，評估結(jié)果的離散程度。較大的離散度通常意味著更高的波動風險。
- 風險價值度量(VaR)：在給定置信水平下估計特定時間范圍內(nèi)的最大潛在損失。例如，95%置信水平下的VaR值表示在正常市場條件下的最大可能損失限額。
- 條件風險價值(ETL)：又稱條件VaR，計算超出VaR閾值的平均損失水平，提供了尾部風險的更全面度量。
量化投資決策實例
假設進行一項10,000英鎊的標準普爾500指數(shù)投資，我們需要通過蒙特卡洛模擬進行風險評估。具體目標包括：
- 在95%置信水平下，年度最大損失不超過2,000英鎊（95% VaR約束）
- 實現(xiàn)至少10%年化收益的概率不低于50%
首先對模擬參數(shù)進行配置：
# 設置模擬參數(shù)
daily_returns = df["adjusted_close"].pct_change().dropna()
# 基礎參數(shù)配置
initial_investment = 10000 # 初始投資金額
num_simulations = 1000 # 模擬路徑數(shù)量
forecast_days = 365 # 預測期限（日）
desired_return = 0.10 # 目標收益率
# 計算收益率統(tǒng)計特征
average_daily_return = daily_returns.mean()
volatility = daily_returns.std()
print(f"Average Daily Return: {average_daily_return}")
print(f"Volatility: {volatility}")
需要注意的是，如果考慮對數(shù)正態(tài)收益假設，可以采用以下方法計算收益率：
daily_returns = np.log(df["adjusted_close"] / df["adjusted_close"].shift(1)).dropna()優(yōu)化后的模擬實現(xiàn)代碼如下：
# 執(zhí)行收益率模擬
simulated_end_returns = np.zeros(num_simulations)
for i in range(num_simulations):
random_returns = np.random.normal(average_daily_return, volatility, forecast_days)
cumulative_return = np.prod(1 + random_returns)
simulated_end_returns[i] = initial_investment * cumulative_return
# 計算最終投資價值
final_investment_values = simulated_end_returns
print(final_investment_values)
第二部分：風險指標的量化分析
風險價值與條件風險價值的計算實現(xiàn)
以下代碼實現(xiàn)了基于模擬結(jié)果的風險價值(VaR)和條件風險價值(CVaR)的計算：
confidence_level = 0.95
sorted_returns = np.sort(final_investment_values)
index_at_var = int((1-confidence_level) * num_simulations)
var = initial_investment - sorted_returns[index_at_var]
conditional_var = initial_investment - sorted_returns[:index_at_var].mean()
print(f"Value at Risk (95% confidence): ￡{var:,.2f}")
print(f"Expected Tail Loss (Conditional VaR): ￡{conditional_var:,.2f}")
風險指標的技術解讀
風險價值(VaR)和條件風險價值(CVaR)提供了不同維度的風險度量，它們的技術含義如下：
風險價值(VaR)分析
示例中顯示的"風險價值(95%置信度)：￡-1,926.81"表明：基于歷史數(shù)據(jù)和當前市場條件，在95%的置信水平下，投資組合在指定持有期內(nèi)的潛在最大損失不會超過1,926.81英鎊。這一指標為投資者提供了在正常市場條件下的風險暴露上限。
條件風險價值(CVaR)分析
"條件風險價值：￡-1,301.08"代表了VaR閾值之外（即最不利的5%情景）的平均損失水平。這一指標提供了對尾部風險更為敏感的度量，有助于評估極端市場條件下的風險暴露。
目標收益實現(xiàn)概率分析
num_success = np.sum(final_investment_values >= initial_investment * (1 + desired_return))
probability_of_success = num_success / num_simulations
print(f"Probability of achieving at least a {desired_return*100}% return: {probability_of_success*100:.2f}%")
投資結(jié)果分布的可視化分析
以下代碼實現(xiàn)了投資結(jié)果的直方圖展示，并標注了關鍵風險和收益閾值：
plt.figure(figsize=(10, 6))
plt.hist(final_investment_values, bins=50, alpha=0.75)
plt.axvline(
initial_investment * (1 + desired_return),
color="r",
linestyle="dashed",
linewidth=2,
)
plt.axvline(initial_investment - var, color="g", linestyle="dashed", linewidth=2)
plt.title("Distribution of Final Investment Values")
plt.xlabel("Final Investment Value")
plt.ylabel("Frequency")
plt.show()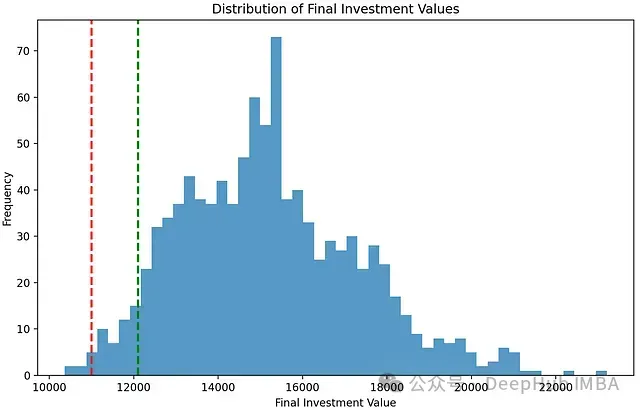
該直方圖中的垂直參考線具有重要的技術含義：
收益目標線（紅色虛線）
- 技術定義：表示達到目標收益率時的投資價值水平
- 計算方法：initial_investment * (1 + desired_return)
- 分析意義：該線右側(cè)的分布區(qū)域代表實現(xiàn)預期收益目標的情景，其面積與目標實現(xiàn)概率直接相關
風險閾值線（綠色虛線）
- 技術定義：表示95%置信水平下的VaR閾值位置
- 計算方法：initial_investment - var
- 分析意義：該線左側(cè)的分布區(qū)域代表超出預期風險容忍度的極端損失情景，其面積為5%
通過這種可視化方法，可以直觀地評估：
- 投資結(jié)果的概率分布特征
- 實現(xiàn)目標收益的可能性
- 極端損失情景的發(fā)生頻率和程度
完整模型實現(xiàn)代碼
以下是整個投資風險分析模型的完整Python實現(xiàn)：
import numpy as np
import matplotlib.pyplot as plt
from eodhd import APIClient
import config as cfg
api = APIClient(cfg.API_KEY)
def get_ohlc_data():
df = api.get_historical_data("GSPC.INDX", "d", results=365)
return df
if __name__ == "__main__":
df = get_ohlc_data()
# 計算日收益率序列
daily_returns = df["adjusted_close"].pct_change().dropna()
# 基礎參數(shù)配置
initial_investment = 10000 # 初始投資金額
num_simulations = 1000 # 模擬路徑數(shù)量
forecast_days = 365 # 預測期限（日）
desired_return = 0.10 # 目標收益率
# 計算收益率統(tǒng)計特征
average_daily_return = daily_returns.mean()
volatility = daily_returns.std()
print(f"Average Daily Return: {average_daily_return}")
print(f"Volatility: {volatility}")
# 執(zhí)行收益率模擬
simulated_end_returns = np.zeros(num_simulations)
for i in range(num_simulations):
random_returns = np.random.normal(
average_daily_return, volatility, forecast_days
)
cumulative_return = np.prod(1 + random_returns)
simulated_end_returns[i] = initial_investment * cumulative_return
# 計算最終投資價值
final_investment_values = simulated_end_returns
# 風險指標計算
confidence_level = 0.95
sorted_returns = np.sort(final_investment_values)
index_at_var = int((1 - confidence_level) * num_simulations)
var = initial_investment - sorted_returns[index_at_var]
conditional_var = initial_investment - sorted_returns[:index_at_var].mean()
print(f"Value at Risk (95% confidence): ￡{var:,.2f}")
print(f"Expected Tail Loss (Conditional VaR): ￡{conditional_var:,.2f}")
# 目標收益實現(xiàn)概率分析
num_success = np.sum(
final_investment_values >= initial_investment * (1 + desired_return)
)
probability_of_success = num_success / num_simulations
print(
f"Probability of achieving at least a {desired_return*100}% return: {probability_of_success*100:.2f}%"
)
# 結(jié)果分布可視化
plt.figure(figsize=(10, 6))
plt.hist(final_investment_values, bins=50, alpha=0.75)
plt.axvline(
initial_investment * (1 + desired_return),
color="r",
linestyle="dashed",
linewidth=2,
)
plt.axvline(initial_investment - var, color="g", linestyle="dashed", linewidth=2)
plt.title("Distribution of Final Investment Values")
plt.xlabel("Final Investment Value")
plt.ylabel("Frequency")
plt.show()責任編輯：華軒
來源：
DeepHub IMBA
