經典算法:無序數組尋找第K大的數值
1. 尋找第K大
題意
有一個無序整數數組,請你根據排序思路,找出數組中第K大的數。
給定一個整數數組a, 請返回第K (1<=K<=n) 大的數(包括重復的元素,不用去重),保證答案存在。
示例
- 輸入 [3,2,1,5,6,4] , 2
- 返回值 5
2. 常規思路
先對無序數組進行排序,然后對有序數組進行查找。
至于選擇什么排序算法,有待確定。
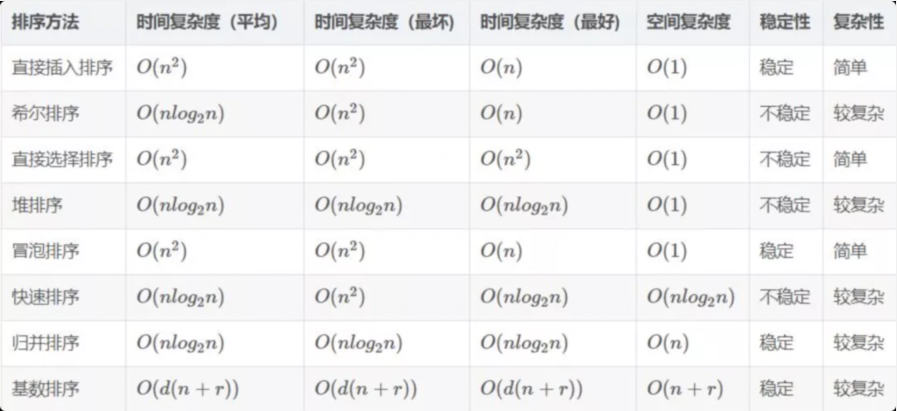
先看一下,各種排序算法的復雜度以及穩定性。
看完上面比較之后,可能你心中已經有了自己的答案。
3. 解題思路
常規思路需要兩大步:
- 先整體排序
- 在有序中查找目標值
那么,針對這道題,我們能不能在排序的過程中就確定目標值呢?
思考一下快排的二分特性:
- 先找出一個數值的位置,該數值的左側比自己小,右側比自己大(整個數組一分為二)
- 再分別進行左、右兩部分進行步驟1的操作,直至整個數組有序。
這里需要知道的是,在快排中某個數值左側比自己小,右側比自己大。該數值的位置就是在最終有序數組中的位置,也就是說可以在查找中確定目標位置。并且,在本題的處理過程中,平均情況下只處理1/2的數據量。
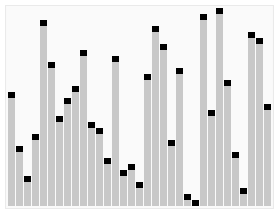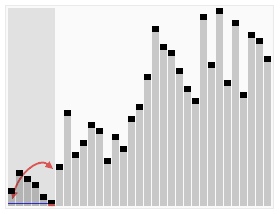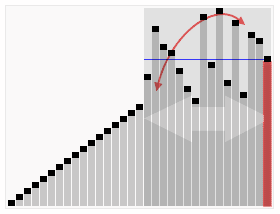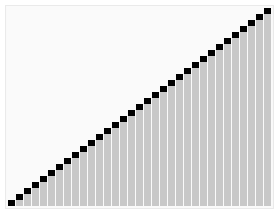
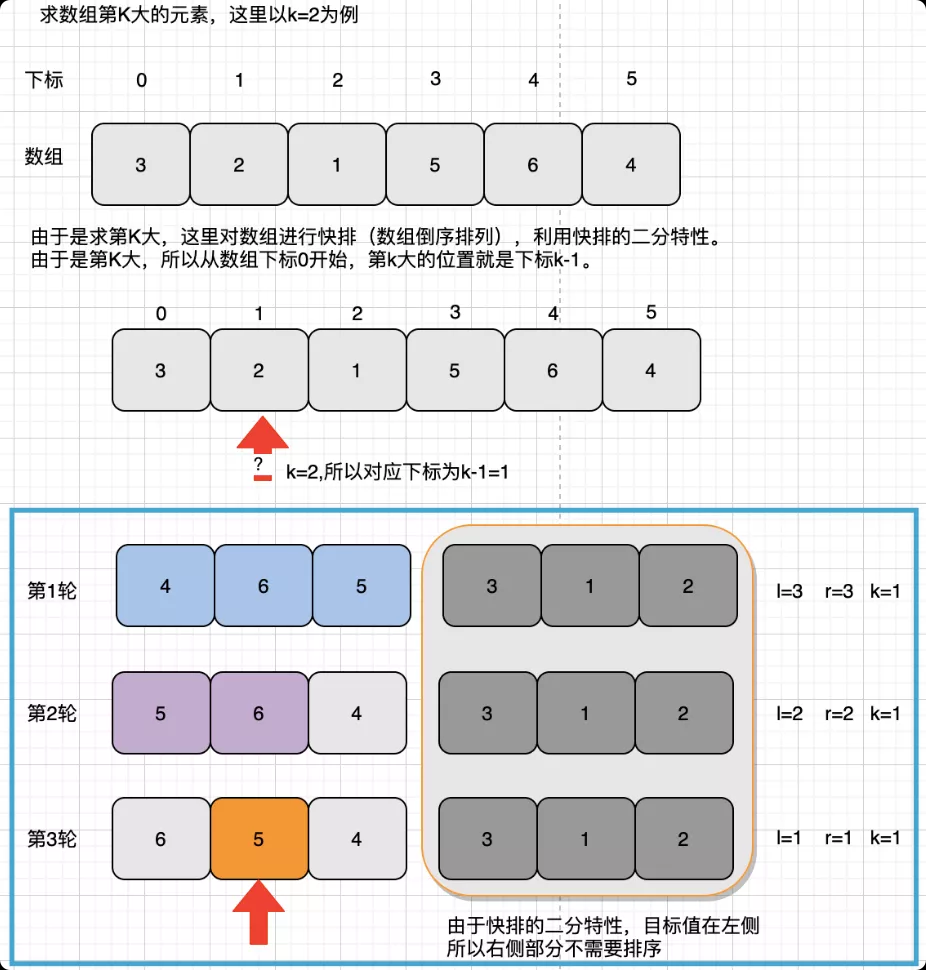
動圖 - 快排算法
快排算法查找過程:
4. Go代碼實現
- func findKLargest(arr []int, k int) int {
- iflen(arr) == 0 || k > len(arr) {
- return-1
- }
- var find func(k int, l, r int) int
- find = func(k int, l, r int) int {
- /*
- // 對于正常的快排,需要下面的代碼
- if l >= r {
- return
- }
- // 然而這里不需要,在尋找第k大的數據時 一般是 l==r
- */
- ll := l
- rr := r
- target := arr[l]
- // 倒序(第K大使用)排列 是 target >= arr[r] / target <= arr[l]
- // 正序(第k小使用)排列 是 target <= arr[r] / target >= arr[l]
- for l < r {
- for l < r && target >= arr[r] {
- r--
- }
- arr[l] = arr[r]
- for l < r && target <= arr[l] {
- l++
- }
- arr[r] = arr[l]
- }
- arr[l] = target
- // k在l的右側
- // 為什么 下面無論是在左右側,第一個參數都是k呢?
- // 因為,k指的是要找的數值的下標位置(第k大就是下標k-1)
- // 無論在左右側,對于數組arr來說,其對應的下標都是固定的
- // 并且 l/r 每次都會變動,所以k這里是固定的
- if k > l {
- // 這里的 l+1, rr 也是數組的下標
- return find(k, l+1, rr)
- }elseif k < l {
- // k在l的左側
- // 這里的 ll, l-1 也是數組的下標
- return find(k, ll, l-1)
- }
- // 此時目標自位置l處的target,就是第k個大的數值
- return target
- }
- // 第k大的數值,對應排序之后就是,數組下標k-1
- finds := find(k-1, 0, len(arr)-1)
- return finds
- }
求第K大,則對數組排序排列。
求第K小,則對數組正序排列。
無論如何,都是從頭開始找,這樣處理更簡單。