使用Playground學習數值算法
中學時，沒有什么比數學圖紙更恐怖的了。
許多問題沒有現成解析方案，還有一些問題雖然可以解決，但需要大量的計算工作。這種情況下，你需要算法來輔助。
希望你沒被算法整吐。萬一你真的吐了，也要看到好的一面：又可以再吃頓午餐了:]
在這個教程中，你將學習到算法的概念，以及如何使用它們來解決難以分析的問題。通過playground，很容易使解決方案可視化，易于查看。
即使你不是個數學愛好者，對物理或計算機科學也不大感興趣，你仍會在這個教程中找到一些有意思的東西。你只需要有一些微積分和基礎物理學的知識。
你將學到如何使用數值算法解決兩個困難問題。但是為了講的更清楚點，這兩個問題也可通過解析法解決。算法在解析法無法工作時更為理想，即便如此，通過比較兩種方法，也能更加容易的理解它們的本質。
數值算法是什么？
簡單說來，數值算法是一類解決數學問題的方法，它們不依賴于閉式解析解。
問題來了，什么是閉式解析解？
若有一個公式，我們可以使用已知數，通過有限的操作步驟，可以獲得一個準確的結果，即稱之為閉式解析解。
再簡單點來理解一下：如果你可以使用代數的方式，找到一個表達式來解決一個未知量問題，代入某些已知數即可得到結果，就說明你已經得到了一個閉式解析方法。
何時使用數值算法？
許多問題沒有現成解析方案，還有一些問題雖然可以解決，但需要大量的計算工作。這種情況下，你需要算法來輔助。
例如，假定你需要編寫一個物理引擎，用來計算許多物體在有限時間內的行為。這時你就可以使用數值算法來更快地得到結果。
這樣做也有副作用，更快的計算速度意味著結果不會十分精確。然而，大多數情況下，這樣的結果已經夠用了。
天氣預報就得益于數值計算。天氣變化的速度、影響因素的數量都是十分驚人的。這是一個非常復雜的系統，只有數值模擬才能完成預知未來的任務。
可能正是因為缺乏這些算法，你的iPhone總是告訴你要下雨了，而外面還是艷陽高照。
開始
作為熱身活動，我們來玩個游戲，接下來，你將計算出一個給定數字的平方根。這兩個方法都將使用二分法（bisection method）。神奇的是，你可能已經知道了這個方法，但是不知道它的名字。
回想一下，在兒童時代，我們可能玩過這樣的游戲：選中100以內的一個數字，另外一個人來猜。你只會提示他猜的數字大了或者小了。
游戲開始。小明告訴小強開始猜，小強說我猜1，小明說小了，小強又猜2，小明說小了。小強接下來再猜3,4...最后選中了5，終于對了。
5步就猜中了，不錯。但是如果小明選的是78，猜中就需要花點時間。
這個游戲如果使用二分法（bisection method）來玩的話，猜中的速度會快很多。
二分法
我們知道數字介于1和100之間，因此除了一個一個的猜，或者隨便瞎猜外。我們把數字分為兩個區間：a = [1,50], b = [51, 100]。
接下來我們判斷數字是介于哪一個區間，這很簡單，只用問數字是不是50。如果數字小于50，那么區間b就不用考慮了。接下來我們繼續把a區間分成兩半，再重復這個步驟。
例如：
數字是60.區間為：a = [1,50], b = [51, 100]。
第一步，小強說50（也即是a區間的上限），小明說小了。這時小強就知道了數字肯定在b區間上。
第二步，分解b區間為： c=[51,75]，d=[76,100]。還是選擇c區間的上限75，小強告訴他大了。這就意味著數字肯定在c區間上。
繼續分解。。。
使用這個方法，7次嘗試即可得到正確答案，一個一個試則需要60次。
1. 50 -> 小了
2. 75 -> 大了
3. 62 -> 大了
4. 56 -> 小了
5. 59 -> 小了
6. 61 -> 大了
7. 60 -> 對了！
計算x的平方根，過程也類似。數字x的平方根介于0和x之間。也可以記做：(0,x]。如果數字x大于或等于1，可以記做：[1, x]。
分解區間，得到a=(0, x/2]，b=(x/2, x]。
如果數字x是9，區間是[1, 9]，分解后的區間為a=[1, 5]，b=(5, 9]，中間值m為(1+9)/2 = 5。
下一步，檢查m * m - x，是否大于期望的精度。在這里，我們檢查m * m 大于或小于等于x。如果大于，我們使用(0, x/2]區間繼續檢查，否則，使用(x/2, x]區間。
看一下實際步驟，初始化m=5, 期望準確值為0.1:
1. 計算m * m - x: 5 * 5 - 9 = 11
2. 檢查結果是否小于等于期望值：25 - 11 <= 0.1?
3. 顯然不滿足，繼續下一個區間：m * m是否大于9？是。接下來使用區間[1, 5]，測試值為(1+5)/2=3。
4. 計算m * m - x：３* 3 - 9 = 0
5. 查查是否滿足期望值：9 - 9 <= 0.1?
6. 搞定。
備注：你可能想知道括號是什么意思？區間有固定的格式（下限和上限）。不同的括號代表不同的區間邊界。圓括號表示邊界不在區間范圍內（即開區間），而方括號表示邊界在區間范圍內（閉區間）。如(0, a] 包含a而不包含0.在上面的例子中：區間 (0, a/2]包含a/2而不包含0；區間(a/2, a]表示所有大于a/2, 小于a的數。
在Playground上使用二分法
現在，是時候應用學到的理論了。我們來自己實現二分算法。創建一個新的playground文件，添加如下的代碼：
- func bisection(x: Double) -> Double {
- //1
- var lower = 1.0
- //2
- var upper = x
- //3
- var m = (lower + upper) / 2
- var epsilon = 1e-10
- //4
- while (fabs(m * m - x) > epsilon) {
- //5
- m = (lower + upper) / 2
- if m * m > x {
- upper = m
- } else {
- lower = m
- }
- }
- return m
- }
1. 設置區間下限為1
2. 設置區間上限為x
3. 找到中間值，并定義期望精確度
4. 檢查操作是否能滿足精確度
5. 如果不滿足，找到新的中間值，定義新的區間，繼續查找。
添加如下代碼來測試該函數：
- let bis = bisection(2.5)
在 m = (lower + upper) / 2這一行的右邊，可以看到代碼執行了35次，意味著找到結果需要35步。
#p#
馬上我們就能看到playground一個可愛功能帶來的好處：數值的完整歷史都可以查看。
二分法可以成功的算出實際結果的近似值。通過數值的歷史記錄圖，就可以看到數值算法是如何逼近正確的解。
按下option+cmd+enter打開輔助編輯器，點擊m = (lower + upper) / 2代碼行右邊的圓按鈕在輔助編輯器中添加歷史記錄。
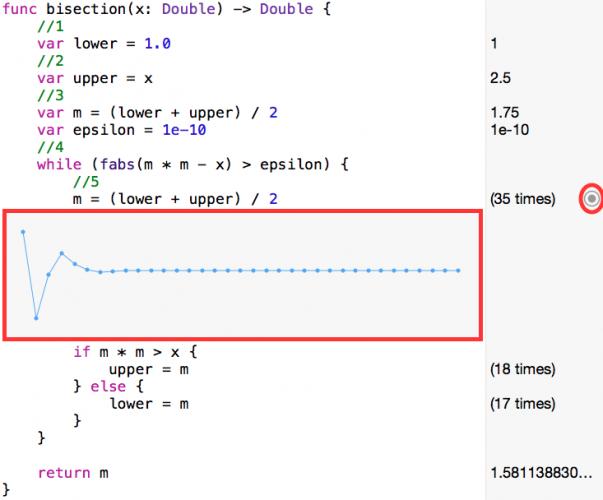
你會看到方法一點點的跳轉到正確結果上。
古典數學也搞的定
下一個算法需要追溯到古代，它起源于公元前1750年的古巴比倫，在公元100年前亞歷山大的希羅所著《度量論》（Metrica ）一書中有所描述。這就是為何它被稱作“希羅方法”。可以通過這個 鏈接 了解更多關于希羅的知識。
這個方法使用函數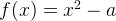
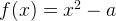，這里你想要計算a的平方根。如果你能找到函數曲線的“0值點（zero point）”，這個點上的函數值為0，那么求出x值就能得到a的平方根。
要完成這項工作，我們首先選擇任意x值作為起始值，計算該值對應點的tangent值（函數的切線），然后查看tangent線上的0點（即該直線和x軸的交點）。然后我們使用這個0點再次作為起始值，重復多次直到滿足精度。
因為每計算一次tangent值，都會更加逼近真正的0值，
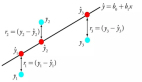
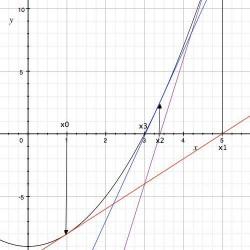
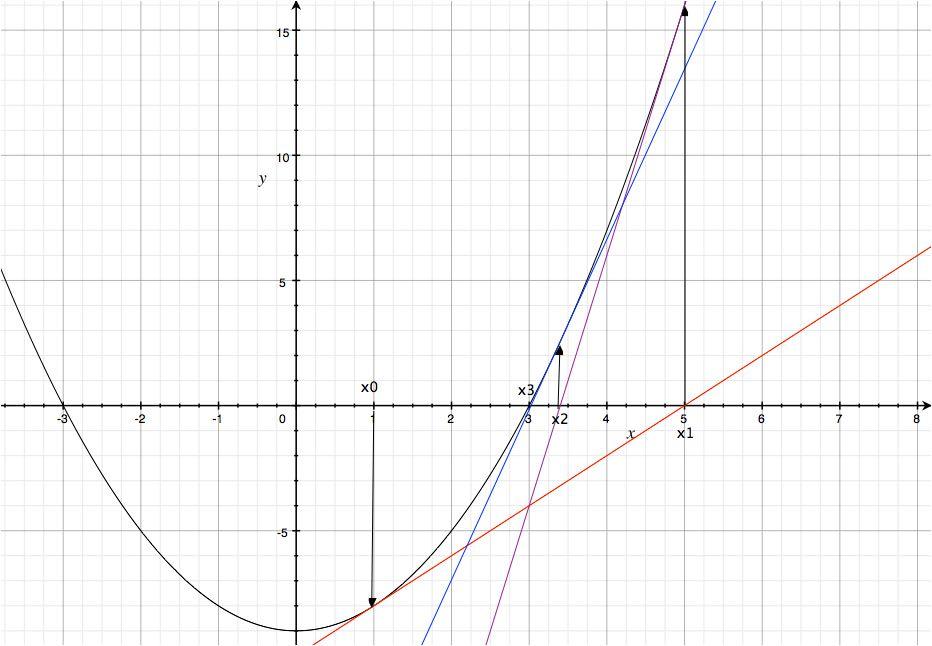
這個過程會逐漸逼近真正的結果。下圖展示了求解a=9時，a的平方根，且起始值為1.
起始點x0 = 1，生成一條紅色的tangent線，接著生成了x1點，又生成了紫色的線；又生成了x2點，連接了藍色的線，最終找到了正確答案。
當古典數學邂逅了Playground
我們有很多古巴比倫人沒有的好東西，比如：playground。在playground上添加如下代碼，并查看：
- func heron(x: Double) -> Double {
- //1
- var xOld = 0.0
- var xNew = (x + 1.0) / 2.0
- var epsilon = 1e-10
- //2
- while (fabs(xNew - xOld) > epsilon) {
- //3
- xOld = xNew
- xNew = (xOld + x / xOld) / 2
- }
- return xNew
- }
這段代碼做了什么？
1. 創建一個變量來存儲當前結果。xOld是上次計算的結果，而xNew是實際結果。
-
找到初始化xNew的方法是一個良好的起點
-
epsilon是期望的精確度
-
這個例子中，我們計算平方根精確度為小數點后10位。
2. 使用while循環查找是否達到期望的精確度。
3. 如果達不到精確度，設置xNew為xOld，繼續下一次迭代。
使用如下代碼驗證該函數的作用：
- let her = heron(2.5)
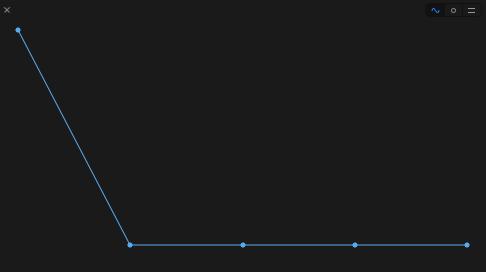
希羅方法只需要5次迭代即可找到正確結果。
在代碼行xNew = (xOld + x/xOld)/2右邊點擊圓角button，添加值歷史，就能看到第一次迭代就能找到一個不錯的近似值。
模擬諧振子運動
在這個章節中，我們來看看如何使用數值積分算法來模擬簡諧系統運動——一種基本的動態系統。
這個系統可以描述很多現象，比如鐘擺的擺動、彈簧的振動。特別說來，它可以描述某段時間內物體移動了一定偏移量的場景。
這個例子中，假定有一個有質量的物體連接在彈簧上。為了簡化問題，我們忽略掉阻力和重力。因此唯一的作用力就是彈簧的彈力，它將物體拉回到原來的位置。
在這樣的假定下，你只需要使用兩個力學定律來處理問題：
-
牛頓第二運動定律
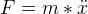, 它描述了物體上的作用力和加速度的關系。 -
胡克定律
，它描述了彈力和物體偏移量之間的比例關系。這里k是彈力系數而x是物體的偏移量。
簡振方程
因為彈力是物體上唯一的作用力，我們將上面的兩個方程式整理：
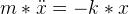
簡化后寫作：
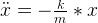
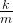也被記作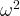
，也即是共振頻率的平方。
更精確的方程式如下：
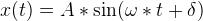
其中A是振幅，這里即是物體的偏移量，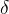
被稱為相位差。這兩個值初始化時都被設置為定值。
如果設置時間t=0，則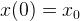
，且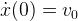
，你可以簡單的計算出振幅和相位差：
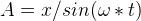
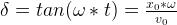
來看一個例子，我們有一個質量為2kg的物體連接在彈簧上，彈簧的彈力系數為k=196N/m。在初始時間t=0時，彈簧移動了0.1米。我們可以通過公式計算振幅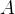
、相差
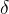和共振頻率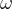
。
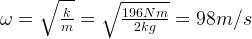
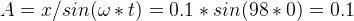
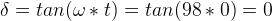
在Playground上實驗一下：
使用該公式計算任意時間點對應的值之前，我們需要添加一些代碼。
回到playground文件，在最后添加如下代碼：
- //1
- typealias Solver = (Double, Double, Double, Double, Double) -> Void
- //2
- struct HarmonicOscillator {
- var kSpring = 0.0
- var mass = 0.0
- var phase = 0.0
- var amplitude = 0.0
- var deltaT = 0.0
- init(kSpring: Double, mass: Double, phase: Double, amplitude: Double, deltaT: Double) {
- self.kSpring = kSpring
- self.mass = mass
- self.phase = phase
- self.amplitude = amplitude
- self.deltaT = deltaT
- }
- //3
- func solveUsingSolver(solver: Solver) {
- solver(kSpring, mass, phase, amplitude, deltaT)
- }
- }
這些代碼塊中做了什么？
1. 定義一個函數類型的的typealias，函數有5個Double類型的參數，返回為空。
2. 創建一個struct來定義諧振子。
3. 這個函數只是簡單的創建用來解振動問題的Clousure。（并無真實的計算代碼）
再來看一下精確方案
代碼如下：
- func solveExact(amplitude: Double, phase: Double, kSpring: Double, mass: Double, t: Double) {
- var x = 0.0
- //1
- let omega = sqrt(kSpring / mass)
- var i = 0.0
- while i < 100.0 {
- //2
- x = amplitude * sin(omega * i + phase)
- i += t
- }
- }
這個方法包含了所有解決運動方程需要的參數。
1. 計算共振頻率
2. 在while循環中計算物體當前的位置，i用作下次計算的自增變量。
添加如下測試代碼：
- let osci = HarmonicOscillator(kSpring: 0.5, mass: 10, phase: 10, amplitude: 50, deltaT: 0.1)
- osci.solveUsingSolver(solveExact)
這個方案中的方法有點奇怪：它有參數傳入，但不返回數據，也沒有顯示任何東西。
#p#
這樣做有什么好處？
使用這個函數的目的在于，在while循環中，可以算出振動過程中具體的動態值。在Playground中，可以觀察這些動態值的歷史記錄。
在x = amplitude * sin(omega * i + phase) 處添加值歷史記錄，我們就能看到運動的軌跡。
既然第一個精確算法已經驗證通過，下面我們看一下數值計算方案。
歐拉方法
歐拉方法是用來求數值積分的一種方法。該方法1768年再Leonhard Euler所著Institutiones Calculi Integralis《積分學原理》一書中首次提出。要查看該方法的詳情，請參考：http://en.wikipedia.org/wiki/Euler_method
歐拉方法的核心思想是通過使用折線逼近曲線。
具體方法是計算一個給定點的斜率，然后繪制一條同樣斜率的折線。在這條折線的末尾，繼續計算斜率，繪制另外一條線。正如你所見，該算法的精確度取決于折線的長度。
你想知道deltaT做了什么嗎？
該數值算法中需要使用一個步長，這對算法的精確度很重要。大步長導致低精確度，但是執行速度塊。反之，精確度會提高，速度會降低。
deltaT變量就代表了步長(step size)。我們初始化這個值為0.1， 意味著我們計算每0.1秒物體移動的位置。在歐拉算法中，意味著折線在x軸上的投影長度為0.1。
在編寫代碼前，你需要再看一下這個公式：
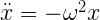
二階微分方程可以轉化為兩個一階微分方程。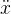
可以被寫為
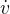和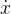
我們可以用差商來完成轉換：
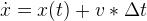
也會得到：
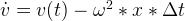
有了這些等式，我們可以直接實現歐拉方法。
在solveExact方法后添加代碼：
- func solveEuler(amplitude: Double, phase: Double, kSpring: Double, mass: Double, t: Double) {
- //1
- var x = amplitude * sin(phase)
- let omega = sqrt(kSpring / mass)
- var i = 0.0
- //2
- var v = amplitude * omega * cos(phase);
- var vold = v
- var xoldEuler = x
- while i < 100 {
- //3
- v -= omega * omega * x * t
- //4
- x += vold * t
- xoldEuler = x
- vold = v
- i+=t
- }
- }
代碼的內容：
1. 設置當前的位置，和omega的值。
2. 計算當前速度。
3. 在while循環中，通過一階函數計算出新的速度。
4. 使用速度計算新的位置，在結束處，使用步長t增加i的值。
現在，添加以下代碼測試：
- osci.solveUsingSolver(solveEuler)
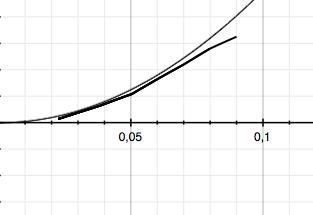
在xoldEuler = x位置添加值歷史，并查看。你會看到這個方法顯示一個振幅增加的正弦函數。因為歐拉方法并不是一個精確算法，而這里過大的步長0.1也導致了計算結果不精確。
以下是另外一個函數圖像，步長為0.01，這樣明顯更好。因此，使用歐拉方法時你要想到，步長越小，結果越好。但是使用折中的步長，執行起來更為簡單。
速度Verlet算法(Velocity Verlet)
最后討論的算法叫做速度Verlet。它和歐拉方法的思路一樣，但是計算新位置的方式有些許差異。
歐拉在計算新位置時，忽略實際的加速度，公式為：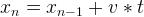
,而速度Verlet算法在計算時考慮到了加速度：
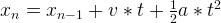。這再步長相等的時候，結果更優。
在solveEuler方法后添加新的代碼：
- func solveVerlet(amplitude: Double, phase: Double, kSpring: Double, mass: Double, t: Double) {
- //1
- var x = amplitude * sin(phase)
- var xoldVerlet = x
- let omega = sqrt(kSpring / mass)
- var v = amplitude * omega * cos(phase)
- var vold = v
- var i = 0.0
- while i < 100 {
- //2
- x = xoldVerlet + v * t + 0.5 * omega * omega * t * t
- v -= omega * omega * x * t
- xoldVerlet = x
- i+=t
- }
- }
代碼的內容：
1. 循環前的所有代碼和歐拉方法中的一樣。
2. 根據速度計算出新的位置，增加i的值。
在Playground中測試代碼:
- osci.solveUsingSolver(solveVerlet)
接下來做什么？
你可以通過 此鏈接 下載完整工程.
希望你在這場數值世界旅行中獲得樂趣。了解一些算法，即便只是一些古典數學的趣味歷史，都會對你帶來幫助。
