終于有人把卷積神經網絡(CNN)講明白了
傳統神經網絡層之間都采用全連接方式,如果采樣數據層數較多,且輸入又是高維數據,那么其參數數量可能將是一個天文數字。
比如訓練一張1000×1000像素的灰色圖片,輸入節點數就是1000×1000,如果隱藏層節點是100,那么輸入層到隱藏層間的權重矩陣就是1000000×100!如果還要增加隱藏層,進行反向傳播,那結果可想而知。不止如此,采用全連接方式還容易導致過擬合。
因此,為更有效地處理圖片、視頻、音頻、自然語言等數據信息,必須另辟蹊徑。經過多年不懈努力,人們終于找到了一些有效方法及工具。其中卷積神經網絡就是典型代表。
01 卷積網絡的一般架構
卷積神經網絡(Convolutional Neural Network,CNN)是一種前饋神經網絡,最早在1986年BP算法中提出。1989年LeCun將其運用到多層神經網絡中,但直到1998年LeCun提出LeNet-5模型,神經網絡的雛形才基本形成。
在接下來近十年的時間里,對卷積神經網絡的相關研究一直處于低谷,原因有兩個:一是研究人員意識到多層神經網絡在進行BP訓練時的計算量極大,以當時的硬件計算能力完全不可能實現;二是包括SVM在內的淺層機器學習算法也開始嶄露頭角。
2006年,Hinton一鳴驚人,在《科學》上發表名為Reducing the Dimensionality of Data with Neural Networks的文章,CNN再度覺醒,并取得長足發展。2012年,CNN在ImageNet大賽上奪冠。
2014年,谷歌研發出20層的VGG模型。同年,DeepFace、DeepID模型橫空出世,直接將LFW數據庫上的人臉識別、人臉認證的正確率提高到99.75%,超越人類平均水平。
卷積神經網絡由一個或多個卷積層和頂端的全連接層(對應經典的神經網絡)組成,同時也包括關聯權重和池化層(Pooling Layer)等。與其他深度學習架構相比,卷積神經網絡能夠在圖像和語音識別方面給出更好的結果。這一模型也可以使用反向傳播算法進行訓練。
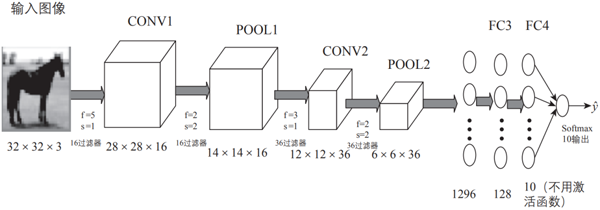
相比其他深度、前饋神經網絡,卷積神經網絡可以用更少的參數獲得更高的性能。圖3-1就是一個簡單的卷積神經網絡架構。
▲圖3-1 卷積神經網絡示意圖
如圖3-1所示,該架構包括卷積神經網絡的常用層,如卷積層、池化層、全連接層和輸出層;有時也會包括其他層,如正則化層、高級層等。接下來我們就各層的結構、原理等進行詳細說明。
圖3-1是用一個比較簡單的卷積神經網絡對手寫輸入數據進行分類的架構示意圖,由卷積層、池化層和全連接層疊加而成。下面我們先用代碼定義這個卷積神經網絡,然后介紹各部分的定義及實現原理。
02 增加通道的魅力
增加通道實際就是增加卷積核,它是整個卷積過程的核心。比較簡單的卷積核或過濾器有垂直邊緣過濾器(Vertical Filter)、水平邊緣過濾器(Horizontal Filter)、Sobel過濾器(Sobel Filter)等。
這些過濾器能夠檢測圖像的垂直邊緣、水平邊緣,增強圖片中心區域權重等。下面我們通過一些圖來簡單演示這些過濾器的具體作用。
1. 垂直邊緣檢測
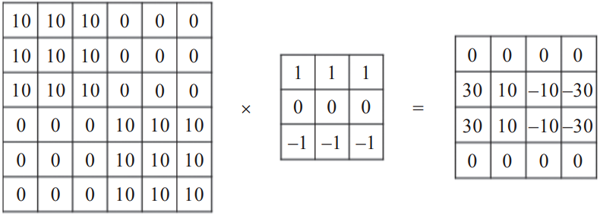
垂直邊緣過濾器是3×3矩陣(注意,過濾器一般是奇數階矩陣),特點是有值的是第1列和第3列,第2列為0,可用于檢測原數據的垂直邊緣,如圖3-2所示。
▲圖3-2 過濾器對垂直邊緣的檢測
2. 水平邊緣檢測
水平邊緣過濾器也是3×3矩陣,特點是有值的是第1行和第3行,第2行為0,可用于檢測原數據的水平邊緣,如圖3-3所示。
▲圖3-3 過濾器對水平邊緣的檢測
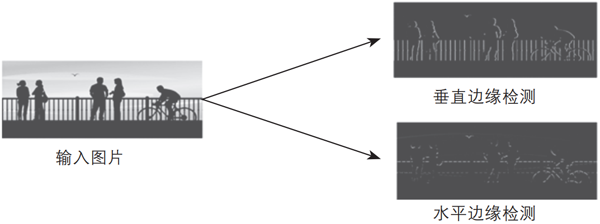
以上兩種過濾器對圖像水平邊緣檢測、垂直邊緣檢測的效果圖如圖3-4所示。
▲圖3-4 過濾器對圖像水平邊緣檢測、垂直邊緣檢測后的效果圖
上面介紹的兩種過濾器比較簡單,在深度學習中,過濾器除了需要檢測垂直邊緣、水平邊緣等,還需要檢測其他邊緣特征。
那么,如何確定過濾器呢?過濾器類似于標準神經網絡中的權重矩陣W,W需要通過梯度下降算法反復迭代求得,所以,在深度學習中,過濾器也需要通過模型訓練得到。卷積神經網絡計算出這些過濾器的數值,也就實現了對圖片所有邊緣特征的檢測。
03 加深網絡的動機
加深網絡的好處包括減少參數的數量,擴大感受野(Receptive Field,給神經元施加變化的某個局部空間區域)。
感受野是指卷積神經網絡每一層輸出的特征圖(Feature Map)上的像素點在輸入圖片上映射的區域大小。通俗點說,感受野是特征圖上每一個點對應輸入圖上的區域,如圖3-5所示。
▲圖3-5 增加網絡層擴大感受野示意圖
由圖3-5可以看出,經過幾個卷積層之后,一個特征所表示的信息量越來越多,一個s3表現了x1、x2、x3、x4、x5的信息。
此外,疊加層可進一步提高網絡的表現力。這是因為它向網絡添加了基于激活函數的“非線性”表現力,通過非線性函數的疊加,可以表現更加復雜的內容。
不同層提取圖像的特征是不一樣的,層數越高,表現的特征越復雜,如圖3-6所示。
▲圖3-6 不同層表現不同的特征
從圖3-6可以看出,前面的層提取的特征比較簡單,是一些顏色、邊緣特征。越往后,提取到的特征越復雜,是一些復雜的幾何形狀。這符合我們對卷積神經網絡的設計初衷,即通過多層卷積完成對圖像的逐層特征提取和抽象。
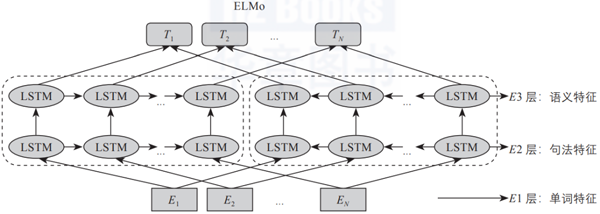
在ELMo預訓練模型中也會存在類似情況,如圖3-7所示,隨著層數的增加,其表示的內容越復雜、抽象。
▲圖3-7 ELMo模型
04 殘差連接
網絡層數增加了,根據導數的鏈式法則,就容易出現梯度消散或爆炸等問題。例如,如果各網絡層激活函數的導數都比較小,那么在多次連乘后梯度可能會越來越小,這就是常說的梯度消散。對于深層網絡來說,傳到淺層,梯度幾乎就沒了。
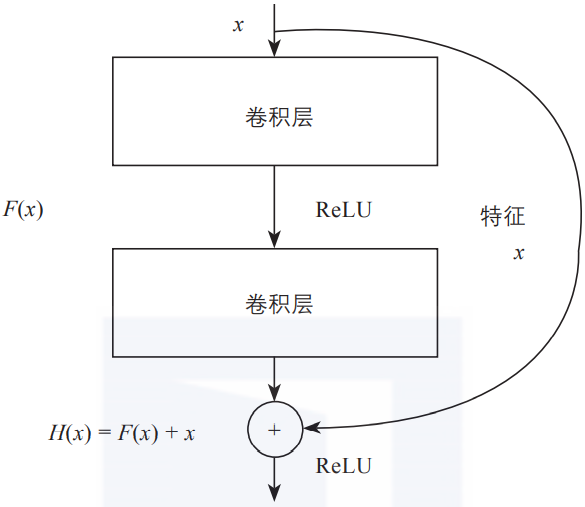
在解決這類問題時,除了采用合適的激活函數外,還有一個重要技巧,即使用殘差連接。圖3-8是殘差連接的簡單示意圖。
▲圖3-8 殘差連接示意圖
如圖3-8所示,圖中的每一個導數都加上了一個恒等項1,dh/dx = d(f + x)/dx = 1 + df/dx。此時就算原來的導數df/dx很小,誤差仍然能夠有效地反向傳播,這也是殘差連接的核心思想。
關于作者:吳茂貴,資深大數據和人工智能技術專家,在BI、數據挖掘與分析、數據倉庫、機器學習等領域工作超過20年。在基于Spark、TensorFlow、PyTorch、Keras等的機器學習和深度學習方面有大量的工程實踐實踐,對Embedding有深入研究。
王紅星,高級數據科學家,任職于博世(中國)投資有限公司蘇州分公司,負責BOSCH數據湖,數據分析與人工智能相關的產品與服務的設計和開發。在大數據、機器學習、人工智能方面有豐富的實踐經驗。
本文摘編自《深入淺出Embedding:原理解析與應用實踐》,經出版方授權發布。