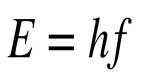作為量子力學(xué)的基礎(chǔ)方程之一，薛定諤方程一直廣受關(guān)注。去年，DeepMind 科學(xué)家開發(fā)一種新的神經(jīng)網(wǎng)絡(luò)來近似計算薛定諤方程，為深度學(xué)習(xí)在量子化學(xué)領(lǐng)域的發(fā)展奠定了基礎(chǔ)。今年九月份，柏林自由大學(xué)的幾位科學(xué)家提出了一種新的深度學(xué)習(xí)波函數(shù)擬設(shè)方法，它可以獲得電子薛定諤方程的近乎精確解。相關(guān)研究發(fā)表在 Nature Chemistry 上。

即使并非物理學(xué)界人士，我們也對薛定諤這個名字并不陌生，比如「薛定諤的貓」。著名物理學(xué)家埃爾溫 · 薛定諤是量子力學(xué)奠基人之一，他在 1926 年提出的薛定諤方程（Schrödinger equation）為量子力學(xué)奠定了堅實的基礎(chǔ)。薛定諤方程是描述物理系統(tǒng)的量子態(tài)怎樣隨時間演化的偏微分方程，是量子力學(xué)的基礎(chǔ)方程之一。

在經(jīng)典力學(xué)里，人們使用牛頓第二定律描述物體運(yùn)動。而在量子力學(xué)里，類似的運(yùn)動方程為薛定諤方程。薛定諤方程的解完備地描述物理系統(tǒng)里微觀尺寸粒子的量子行為，包括分子系統(tǒng)、原子系統(tǒng)、亞原子系統(tǒng)。微觀系統(tǒng)的狀態(tài)由波函數(shù)來描寫，薛定諤方程即是波函數(shù)的微分方程。若給定了初始條件和邊界的條件，就可由此方程解出波函數(shù)。另外，薛定諤方程的解還可完備地描述宏觀系統(tǒng)，可能乃至整個宇宙。

求解薛定諤方程可以為化學(xué)反應(yīng)提供線索。化學(xué)反應(yīng)的結(jié)果基本上與電子以及它們環(huán)繞原子和分子的方式有關(guān)。而控制事物反應(yīng)的能量以及電子在分子中的軌道的差異決定了化學(xué)物質(zhì)的形狀，也由此決定了其性質(zhì)。計算這一能量的方式就是求解薛定諤方程。換句話說，求解出薛定諤方程，就可以知道化學(xué)反應(yīng)的結(jié)果。

然而，這并非易事。此前，我們可以精確求解的原子只有氫原子——僅具備一個質(zhì)子和一個電子。

最近，來自柏林自由大學(xué)的科學(xué)家提出利用人工智能計算薛定諤方程的基態(tài)解，相關(guān)研究發(fā)表在 Nature Chemistry 上。

用 AI 求解薛定諤方程

量子化學(xué)旨在預(yù)測分子的化學(xué)和物理性質(zhì)，它僅利用分子在三維空間中的原子排列來完成。這可以減少對資源的需求，并加快實驗速度。理論上，這可以通過求解薛定諤方程來完成，但在實踐中這往往非常困難。目前，人們?nèi)詿o法高效求得任意分子的精確解。

最近，來自柏林自由大學(xué)的科學(xué)家提出一種深度學(xué)習(xí)方法，達(dá)到了前所未有的計算效率和準(zhǔn)確度權(quán)衡。

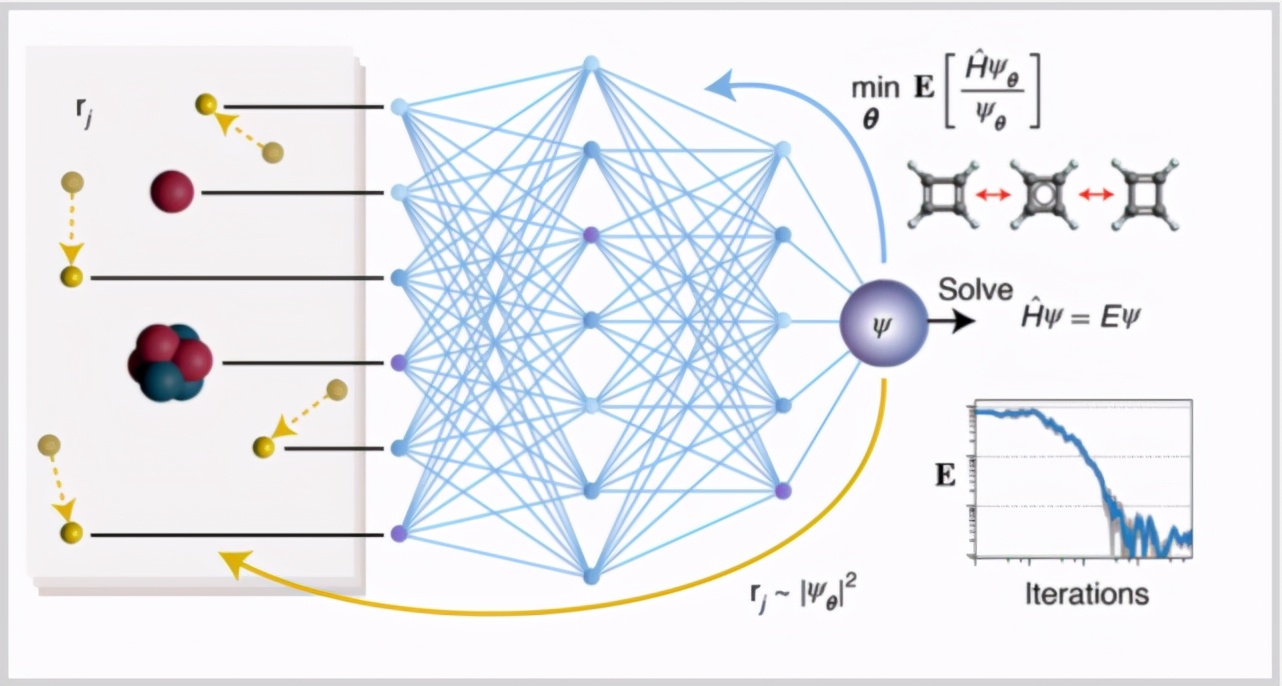
該研究作者之一 Frank Noé 教授表示：「我們認(rèn)為這一方法或?qū)O大地影響量子化學(xué)的未來。」

無需在準(zhǔn)確度和計算成本之間做出取舍

波函數(shù)是量子化學(xué)和薛定諤方程的關(guān)鍵所在，是一種描述分子內(nèi)電子行為的函數(shù)。它是一種高維實體，這使得捕獲編碼特定電子之間相互影響方式的頻譜變得極度困難。

量子化學(xué)領(lǐng)域中的許多方法不再只是嘗試以數(shù)學(xué)方式獲得特定分子的能量，但這需要近似值，限制了預(yù)測的質(zhì)量。還有一些利用大量簡單數(shù)學(xué)構(gòu)造塊表示波函數(shù)的方法，但這些方法過于復(fù)雜，難以針對較多原子計算波函數(shù)。

該研究一作 Jan Hermann 設(shè)計了新方法的關(guān)鍵特征，他表示：「避免在準(zhǔn)確度和計算成本之間進(jìn)行權(quán)衡是量子化學(xué)的最高成就。」

將物理屬性引入 AI 神經(jīng)網(wǎng)絡(luò)

Hermann 表示：「到目前為止，最流行的方法是極具成本效益的密度泛函理論。我們認(rèn)為我們提出的深度『Quantum Monte Carlo』方法至少可以達(dá)到同樣好的效果。該方法以可接受的計算成本提供了前所未有的準(zhǔn)確度。」

該研究設(shè)計了一個深度神經(jīng)網(wǎng)絡(luò)來表示電子的波函數(shù)，這是一種全新的方法。Noé 解釋說：「我們沒有使用用相對簡單的數(shù)學(xué)成分組成波函數(shù)的標(biāo)準(zhǔn)方法，而是設(shè)計了一種人工神經(jīng)網(wǎng)絡(luò)，它能夠?qū)W習(xí)電子圍繞原子核運(yùn)動的復(fù)雜模式。」

Hermann 表示：「電子波函數(shù)的獨(dú)特性在于反對稱性。在交換兩個電子時，波函數(shù)需要改變符號，我們必須將這種特性引入到神經(jīng)網(wǎng)絡(luò)架構(gòu)中才能使之奏效。」

受泡利不相容原理啟發(fā)，PauliNet 方法誕生

受到「泡利不相容原理」（Pauli exclusion principle）的啟發(fā)，研究者將他們的方法命名為「PauliNet」。它是一種深度學(xué)習(xí)波函數(shù)擬設(shè)，可以獲得電子薛定諤方程的近乎精確解。PauliNet 具有一個作為基線的內(nèi)置多參考哈特里－福克（Hartree–Fock）解，集成有效波函數(shù)的物理特性，并使用變分量子蒙特卡羅方法（variational quantum Monte Carlo, VMC）進(jìn)行訓(xùn)練。

PauliNet 擬設(shè)架構(gòu)的信息流如下圖所示：

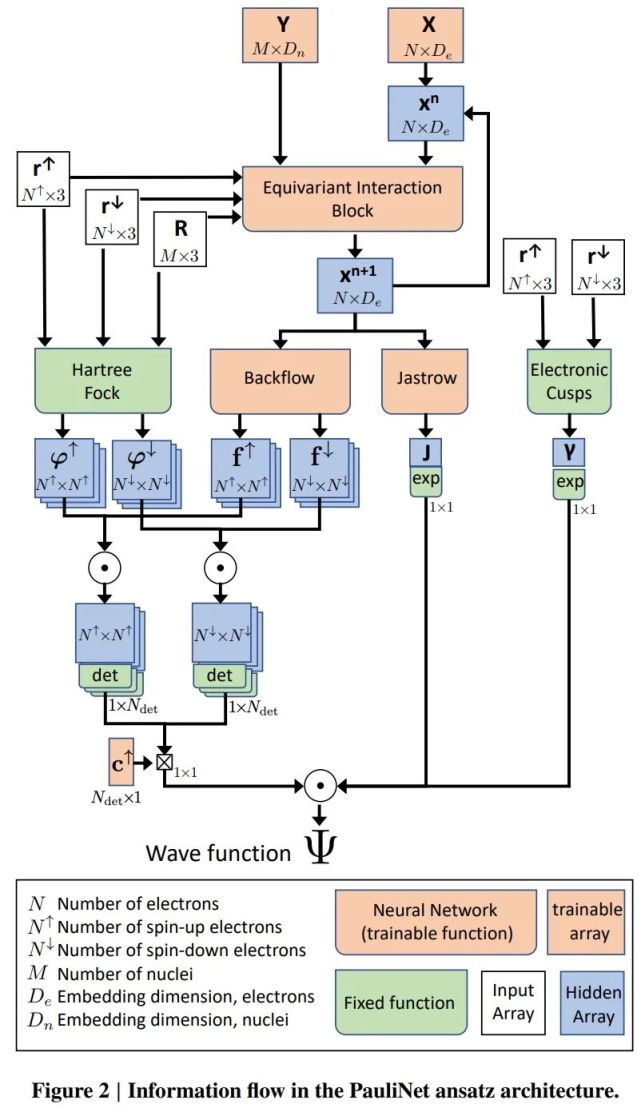
在實驗部分，研究者采用了用于 DeepWF（Han et al., 2019）的相同系統(tǒng)，具體為氫分子（H_2）、氫化鋰（LiH）、鈹（Be）以及硼（B）和線性氫鏈 H_10。研究者將 PauliNet 與 SD-VMC（singledeterminant variational, 標(biāo)準(zhǔn)單行列式變分蒙特卡羅）、SD-DMC（singledeterminant diffusion, 標(biāo)準(zhǔn)單行列式擴(kuò)散蒙特卡羅）和 DeepWF 進(jìn)行了比較。

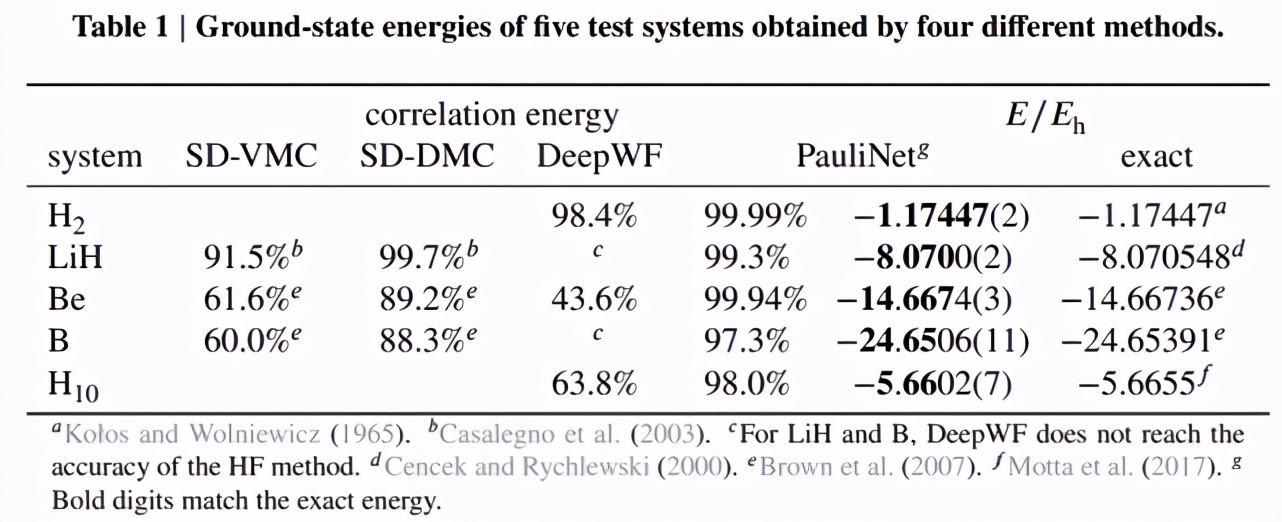
結(jié)果表明，PauliNet 的性能優(yōu)于這三種用于原子、雙原子分子和強(qiáng)相關(guān)氫鏈的 SOTA VMC 擬設(shè)方法，并且具有較高的計算效率。下表 1 為使用這四種不同方法時，H_2、LiH、Be、B 和 H_10 五種系統(tǒng)的基態(tài)能量對比：

求解薛定諤方程的潛在應(yīng)用

研究者預(yù)計，由于系統(tǒng)大小對實驗效果具有正面影響，該方法可能成為中型分子系統(tǒng)上高準(zhǔn)確度電子結(jié)構(gòu)計算的新主導(dǎo)方法。

當(dāng)然，在本研究提出的新方法能夠處理工業(yè)應(yīng)用之前，研究者還有很多需要克服的難題。研究者表示：「這是一項基礎(chǔ)性研究，但對于分子和材料科學(xué)中的古老問題而言卻是一種最新方法。我們很高興該方法創(chuàng)造了無限的可能性。」

求解薛定諤方程在量子化學(xué)領(lǐng)域具有廣泛的應(yīng)用。從計算機(jī)視覺到材料科學(xué)，求解薛定諤方程將會促成人類想象不到的商品發(fā)展。雖然這一革命性創(chuàng)新離落地應(yīng)用還有很長的一段路要走，但這一研究活躍在科學(xué)世界依然令人興奮。