本文經(jīng)AI新媒體量子位（公眾號ID:QbitAI）授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請聯(lián)系出處。

SVM？老分類算法了，輕松拿下。

然而，每一次老板讓你講解SVM，或每一次面試被問到SVM，卻總是結(jié)結(jié)巴巴漏洞百出。

「這些人怎么總能精準(zhǔn)發(fā)現(xiàn)我的盲點(diǎn)？」

簡直讓人懷疑自己掌握的是假SVM。

如果你有這樣的問題，那這篇SVM數(shù)學(xué)原理對你會(huì)有很大幫助，一起來看看吧。

SVM 由線性分類開始

理解SVM，咱們必須先弄清楚一個(gè)概念：線性分類器。

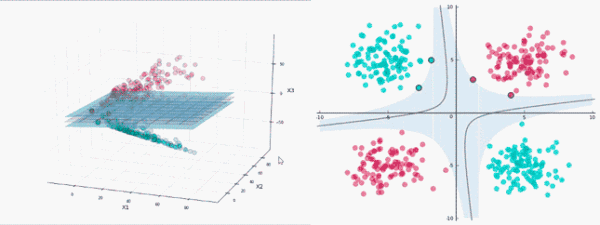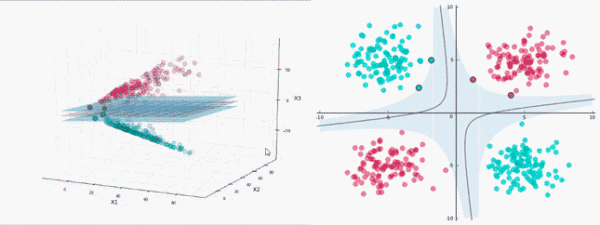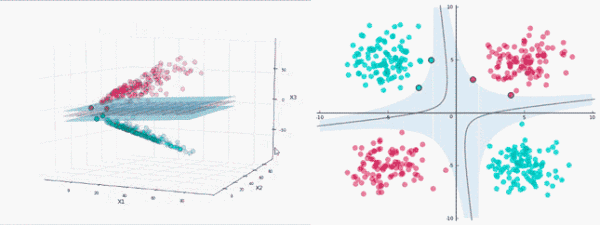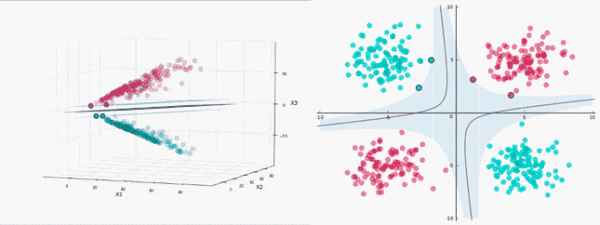
給定一些數(shù)據(jù)點(diǎn)，它們分別屬于兩個(gè)不同的類，現(xiàn)在要找到一個(gè)線性分類器把這些數(shù)據(jù)分成兩類。

如果用x表示數(shù)據(jù)點(diǎn)，用y表示類別（y可以取1或者-1，分別代表兩個(gè)不同的類），一個(gè)線性分類器的目標(biāo)是要在n維的數(shù)據(jù)空間中找到一個(gè)超平面（hyper plane），將x的數(shù)據(jù)點(diǎn)分成兩類，且超平面距離兩邊的數(shù)據(jù)的間隔最大。

這個(gè)超平面的方程可以表示為（ wT中的T代表轉(zhuǎn)置）:

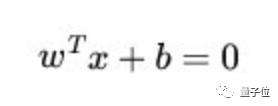
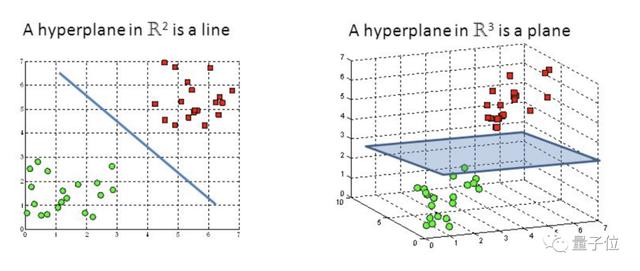
△2維坐標(biāo)系中，超平面是一條直線

當(dāng)f(x)等于0的時(shí)候，x便是位于超平面上的點(diǎn)，而f(x)大于0的點(diǎn)對應(yīng) y=1 的數(shù)據(jù)點(diǎn)，f(x)小于0的點(diǎn)對應(yīng)y=-1的點(diǎn)。

SVM 想要的就是找到各類樣本點(diǎn)到超平面的距離最遠(yuǎn)，也就是找到最大間隔超平面。任意超平面可以用下面這個(gè)線性方程來描述：

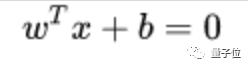
二維空間點(diǎn)（x，y）到直線Ax+By+C=0的距離公式是：

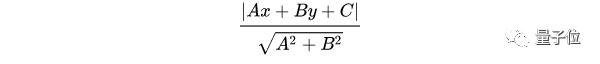
擴(kuò)展到n維空間后，點(diǎn)x=（x1，x2……xn）到直線wTx+b=0的距離為：

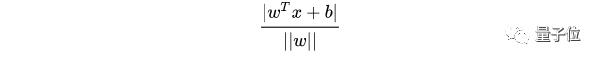
其中 :

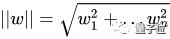
根據(jù)支持向量的定義，支持向量到超平面的距離為d，其他點(diǎn)到超平面的距離大于d。

于是有：

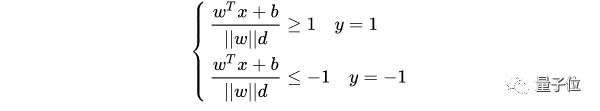
||w||d是正數(shù)，令它為 1（之所以令它等于 1，是為了方便推導(dǎo)和優(yōu)化，且這樣做對目標(biāo)函數(shù)的優(yōu)化沒有影響），于是：

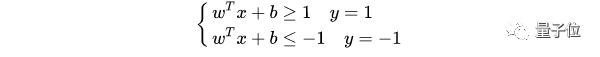
將兩個(gè)方程合并，有：

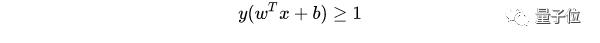
至此，就得到了最大間隔超平面的上下兩個(gè)超平面。

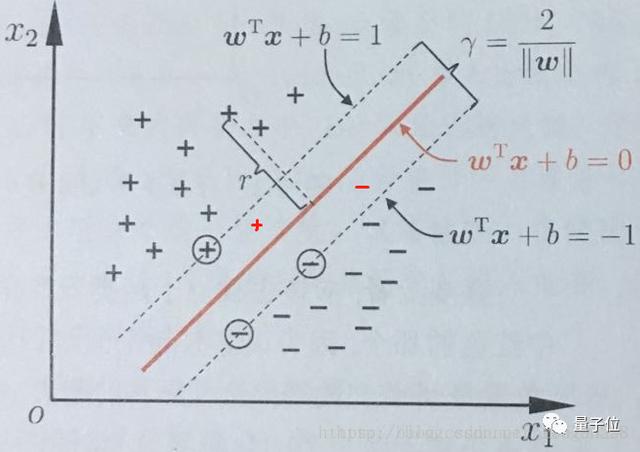
每個(gè)支持向量到超平面的距離可以寫為：

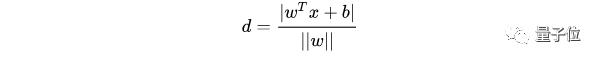
由 y(wTx+b)>1>0 可以得到 y(wTx+b)=|wTx+b|，所以可以將支持向量到超平面距離改寫為：

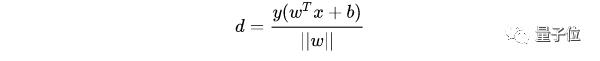
最大化這個(gè)距離：

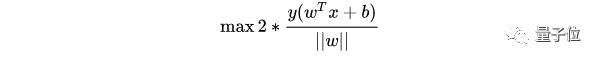
這里乘上 2 倍是為了后面推導(dǎo)方便，對目標(biāo)函數(shù)沒有影響。

帶入一個(gè)支持向量，可以得到：

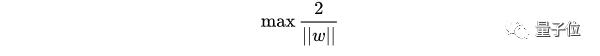
所以得到的最優(yōu)化問題是：

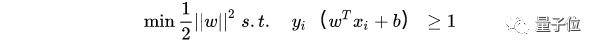
處理異常值

有時(shí)，對于某些點(diǎn)（x（i），y（i）），分類器可能會(huì)做出錯(cuò)誤操作。

盡管在開發(fā)實(shí)際使用的SVM模型時(shí)，會(huì)設(shè)計(jì)冗余，避免過擬合，但仍然需要想辦法將誤差控制在一個(gè)較小的范圍。

可以通過在模型中增加懲罰機(jī)制（用c表示）解決這個(gè)問題。

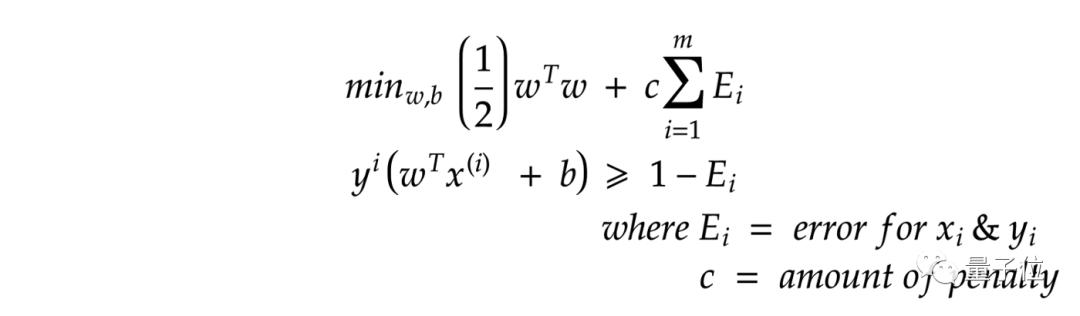
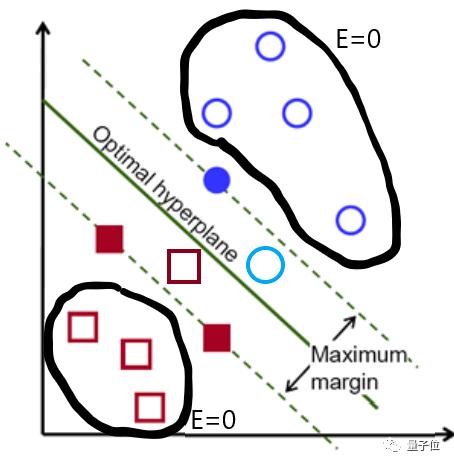
設(shè)SVM輸出結(jié)果為E，則上圖中出現(xiàn)的E=0則沒有懲罰。

若果c非常大，則模型分類更加精準(zhǔn)，但支持向量到超平面距離小，容易出現(xiàn)過擬合。

若c=1，則支持向量到超平面距離最大化，盡管會(huì)出現(xiàn)一些分類誤差，但這是一種較好的方案。

約束凸優(yōu)化問題

為了克服約束凸優(yōu)化問題，采用PEGASOS算法。

重新構(gòu)造一個(gè)約束獨(dú)立性方程：

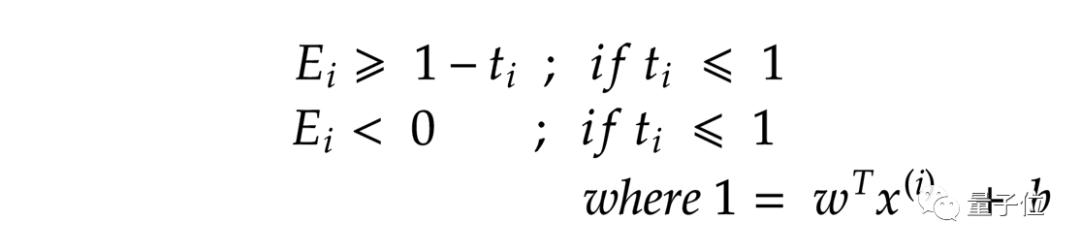
上式表示，如果點(diǎn)遠(yuǎn)離直線，則誤差將為零，否則誤差將為（1-t（i））。

我們需要最小化的是：

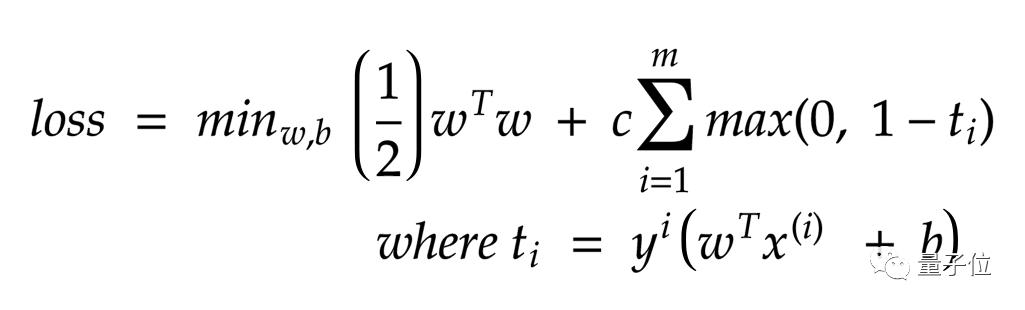
由于消除了約束，因此可以采用梯度下降來最大程度地減少損失。

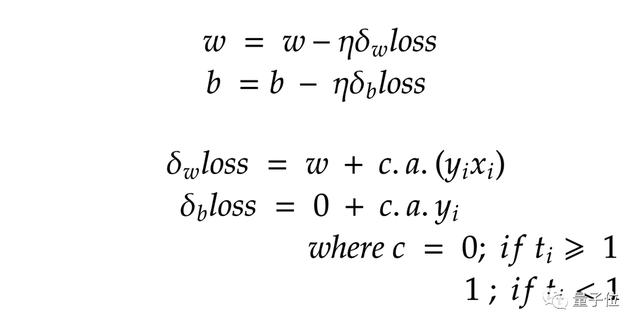
梯度下降算法計(jì)算損失：

在SVM上應(yīng)用梯度下降：

非線性分類

使用SVM對非線性數(shù)據(jù)進(jìn)行分類，需要將數(shù)據(jù)投影到更高的維度，即通過增加低維數(shù)據(jù)的特征向量將其轉(zhuǎn)換為高維數(shù)據(jù)。

增加數(shù)據(jù)特征向量需要消耗巨大的計(jì)算資源，這里采用核函數(shù)。

而這種思路最難的點(diǎn)，是為你自己的模型選擇一個(gè)合適的核函數(shù)。

這里推薦一種自動(dòng)調(diào)參方法GridSearch。

將多種核函數(shù)（線性、RBF、多項(xiàng)式、sigmoid等）等標(biāo)號，依次調(diào)用，找到一個(gè)最合適自己模型的。

定義一個(gè)變量params：

params = [{‘kernel’:[‘linear’, ‘rbf’, ‘poly’, ‘sigmoid’], ‘c’:[0.1, 0.2, 0.5, 1.0, 2.0, 5.0]} 

調(diào)用：

以上詳細(xì)介紹了SVM背后的數(shù)學(xué)原理，并提供了一些使用SVM模型時(shí)的問題解決辦法。

其中，使用代碼自動(dòng)選擇核函數(shù)的方法來自外國博主Daksh Trehan。

如果你對SVM的原理有更深刻的理解，或有其他實(shí)用的技巧，請留言分享給大家吧。