介紹

假設您已經建立了一個面部識別模型，并且現在使用驗證集來調整測試集上的實驗參數。 可悲的是，您的實驗得出的測試結果令人失望。

 

[[330663]]

我們如何知道針對此特定問題的優秀的補救方法是什么?

首先了解假設提升問題，然后看看是否可以從衍生自該算法的AdaBoost算法的結果中提取實用原理，從而解決該問題。

線性預測器

線性回歸

線性回歸建模解釋變量或自變量與標量響應或因變量之間的關系。

使用線性預測函數對關系進行建模。

 

 

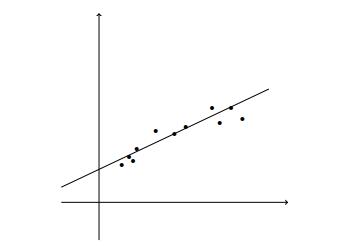
> Linear Regression

回歸的損失函數需要定義由于我們的預測與標簽或目標的真實結果之間的差異而應受到的懲罰。

均方誤差使用平方損失函數來最小化此差異。

 

 

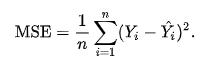
> Mean Squared Error

其中n是預測數，Y是被預測變量的觀測值，而Ŷ是預測值。

一些學習任務需要非線性預測器，例如多項式預測器。

 

 

 

 

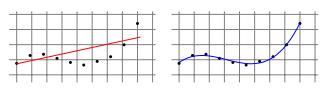
> Linear Regression for Polynomial Regression Tasks

通過使用最小二乘算法找到系數的優秀矢量，可以將這個問題簡化為線性回歸問題，該算法最小化了曲線上各點的偏移的平方和("殘差")。

邏輯回歸

在邏輯回歸中，我們學習對間隔[0，1]上存在的某個類別或事件的概率進行建模。

邏輯函數是一個S型函數，它接受任何實際輸入，并輸出一個介于0和1之間的值。

 

 

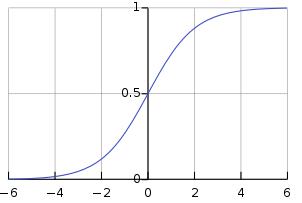
> Sigmoid function

如果此處的學習失敗，我們可以嘗試增強以解決偏差-偏差權衡問題。

假設提振問題

"一組弱學習者可以創造一個單一的強學習者嗎?" —邁克爾·科恩斯(Michael Kerns)和萊斯利·加布里埃爾·萊斯(Leslie Gabriel Valiant)

Boosting使用線性預測變量的泛化來解決以下問題：

偏差-方差權衡

讓我們定義一些術語：

• 近似誤差是我們先驗知識的誤差，或者是我們的算法以何種概率輸出最佳答案。
• 估計誤差是我們的算法將預測看不見數據的結果的誤差。

候選模型越復雜，近似誤差越小，但是估計誤差越大。

通過使學習者從可能具有較大近似誤差的簡單模型開始，發展為使近似誤差和估計誤差均最小的模型，Boosting使學習者可以控制此折衷。

學習的計算復雜性

提升可以提高弱勢學習者或簡單算法的準確性，而簡單算法的性能要比隨機猜測好一點。 這個想法是試圖將弱學習者轉變為強學習者，以便產生一個與難以學習和計算復雜的學習者相當的高效預測器。

自適應提升

AdaBoost(自適應增強)是一種基于理論假設增強問題的算法，該算法將假設的線性組合與檢測圖像中人臉的單個假設組成。

AdaBoost的偽代碼，

 

 

> AdaBoost pseudocode

對于指定的回合數，AdaBoost算法分配權重，該權重與每個假設的誤差成反比。 然后在假設正確的情況下更新此權重，這將獲得較低的概率權重，而與假設不正確的示例相反。 這是針對多個回合執行的，因此，在每個后續回合中，弱學習者會將注意力集中在有問題的樣本上。 然后，這會基于所有弱假設的加權總和產生一個"強分類器"。

其中T是訓練回合的數量，h是弱學習者的運行時間，AdaBoost算法的運行時間有效地為O(Th)。

AdaBoost用于人臉識別

讓我們回到我們的示例，在此示例中，我們要構建一個人臉識別模型，該模型采用24 x 24像素的圖像并使用該信息來確定圖像是否描繪了人臉。

我們將使用代表這四個基本假設的線性函數，

 

 

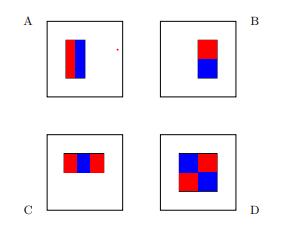
> Base hypotheses for face recognition

每個假設的功能形式包括：

• 軸對齊矩形R，最多24個軸對齊矩形
• A，B，C或D型

并將圖像映射到標量值。

為了計算我們的學習函數，我們計算位于紅色矩形內的像素的灰度值之和，然后從藍色矩形內的像素的灰度值之和中減去該值。

我們可以通過首先在每個圖像上計算函數的所有可能輸出，然后應用AdaBoost算法來實現弱學習者。 這導致強度在臉部區域中增長，這可能導致更好的預測。

模型選擇與驗證

我們已經到了最終解決方案可以選擇幾種模型的地步。

解決我們特定問題的優秀模型是什么?

我們可以將樣本劃分為訓練集和測試集，以便在近似誤差和估計誤差之間找到平衡。 在訓練模型時，我們將使用訓練集，并且將使用獨立測試集來驗證模型，以獲取經驗誤差。 這將使我們有直覺來了解我們是過度擬合，過于緊密地擬合我們的訓練樣本，還是欠擬合而不充分地擬合我們的訓練樣本。

 

 

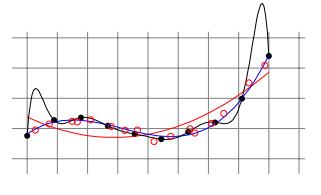
> Validation for model selection on polynomial regressors

近似誤差和估計誤差到底取決于什么?

首先定義一些術語：

• 讓我們的假設類別代表我們可以為機器學習算法選擇的所有可能假設的集合。
• 讓我們將分布定義為未知函數，該函數確定從樣本空間進行任何單獨觀察的真實概率。

我們的近似誤差取決于分布和假設類別。 增加假設類別或使用其他特征表示可能會為我們提供一些替代知識，這些知識可能會改善近似誤差。

我們的估計誤差取決于訓練樣本量。 為了改善估計誤差，我們必須有足夠數量的訓練樣本。 較大的假設類別通常會增加估計誤差，因為這會使找到良好的預測變量更加困難。 AdaBoost算法的結果是產生一個"強分類器"，該分類器基于所有弱假設的加權和，從本質上減少了假設類別。

結論

從線性回歸到自適應提升向我們展示了一個示例，說明如何解決學習成績差的問題是模棱兩可的。

模型選擇，驗證和學習曲線是我們可以用來幫助我們了解學習失敗的原因以便找到補救措施的工具。

很好地總結了以下原則，這些原則直接來自對機器學習的理解：從理論到算法：

1.如果學習涉及參數調整，請繪制模型選擇曲線以確保適當調整了參數。

 

 

 

 

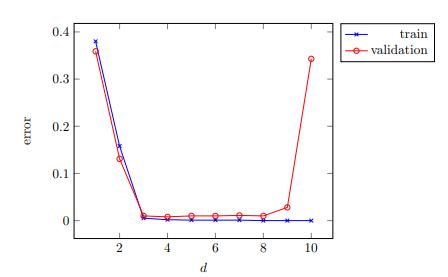
> Model-selection curve

2.如果訓練誤差過大，請考慮擴大假設類別，完全更改它，或更改數據的特征表示。

3.如果訓練誤差較小，則繪制學習曲線并嘗試從中推斷出問題是估計誤差還是近似誤差。

 

 

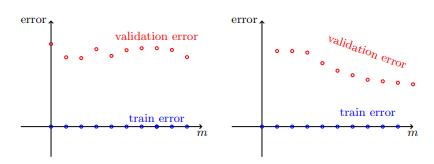
> Learning curves : estimation error vs approximation error

4.如果近似誤差似乎足夠小，請嘗試獲取更多數據。 如果這不可能，請考慮降低假設類別的復雜性。

5.如果近似誤差似乎也很大，請嘗試完全更改假設類別或數據的特征表示。