手把手教你用直方圖、餅圖和條形圖做數據分析(Python代碼)
對于定量數據,要想了解其分布形式是對稱的還是非對稱的、發現某些特大或特小的可疑值,可做出頻率分布表、繪制頻率分布直方圖、繪制莖葉圖進行直觀分析;對于定性數據,可用餅圖和條形圖直觀地顯示其分布情況。
01 定量數據的分布分析
對于定量變量而言,選擇“組數”和“組寬”是做頻率分布分析時最主要的問題,一般按照以下步驟進行:
- 第一步:求極差。
- 第二步:決定組距與組數。
- 第三步:決定分點。
- 第四步:列出頻率分布表。
- 第五步:繪制頻率分布直方圖。
遵循的主要原則如下:
- 各組之間必須是相互排斥的。
- 各組必須將所有的數據包含在內。
- 各組的組寬最好相等。
下面結合具體實例來運用分布分析對定量數據進行特征分析。
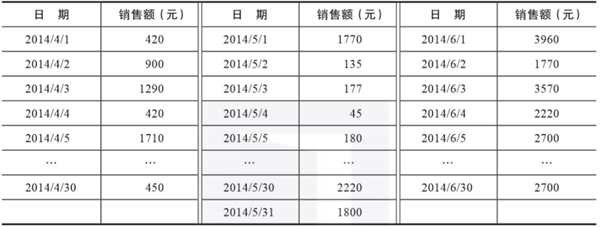
表3-2是菜品“撈起生魚片”在2014年第二個季度的銷售數據,繪制銷售量的頻率分布表、頻率分布圖,對該定量數據做出相應的分析。
▲表3-2 “撈起生魚片”的銷售情況
1. 求極差
極差=最大值-最小值=3960-45=3915
2. 分組
這里根據業務數據的含義,可取組距為500,則組數如下所示。
組數=極差/組距=3915/500=7.83≈8
3. 決定分點
分布區間如表3-3所示。
▲表3-3 分布區間
4. 繪制頻率分布直方表
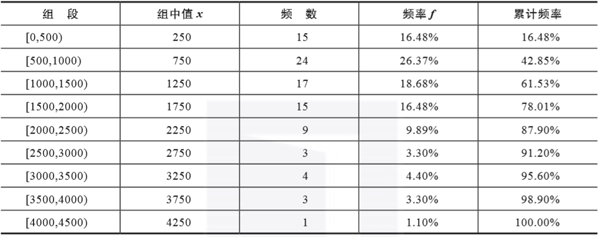
根據分組區間得到如表3-4所示的頻率分布表。
- 其中,第1列將數據所在的范圍分成若干組段,其中第1個組段要包括最小值,最后一個組段要包括最大值。習慣上將各組段設為左閉右開的半開區間,如第一個組段為[0,500)。
- 第2列組中值是各組段的代表值,由本組段的上限值和下限值相加除以2得到。
- 第3列和第4列分別為頻數和頻率。
- 第5列是累計頻率,是否需要計算該列數值視情況而定。
▲表3-4 頻率分布
5. 繪制頻率分布直方圖
若以2014年第二季度“撈起生魚片”這道菜每天的銷售額組段為橫軸,以各組段的頻率密度(頻率與組距之比)為縱軸,表3-4中的數據可繪制成頻率分布直方圖,如代碼清單3-3所示。
- 代碼清單3-3 “撈起生魚片”的季度銷售情況
- import pandas as pd
- import numpy as np
- catering_sale = '../data/catering_fish_congee.xls' # 餐飲數據
- data = pd.read_excel(catering_sale,names=['date','sale']) # 讀取數據,指定“日期”
- 列為索引
- bins = [0,500,1000,1500,2000,2500,3000,3500,4000]
- labels = ['[0,500)','[500,1000)','[1000,1500)','[1500,2000)',
- '[2000,2500)','[2500,3000)','[3000,3500)','[3500,4000)']
- data['sale分層'] = pd.cut(data.sale, bins, labelslabels=labels)
- aggResult = data.groupby(by=['sale分層'])['sale'].agg({'sale': np.size})
- pAggResult = round(aggResult/aggResult.sum(), 2, ) * 100
- import matplotlib.pyplot as plt
- plt.figure(figsize=(10,6)) # 設置圖框大小尺寸
- pAggResult['sale'].plot(kind='bar',width=0.8,fontsize=10) # 繪制頻率直方圖
- plt.rcParams['font.sans-serif'] = ['SimHei'] # 用來正常顯示中文標簽
- plt.title('季度銷售額頻率分布直方圖',fontsize=20)
- plt.show()
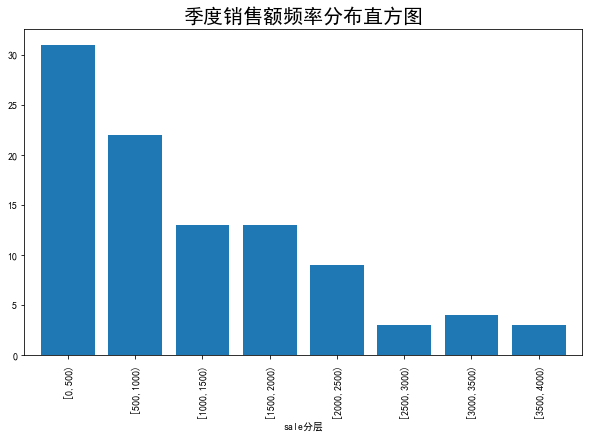
運行代碼清單3-3可得季度銷售額頻率分布直方圖,如圖3-3所示。
▲圖3-3 季度銷售額頻率分布直方圖
02 定性數據的分布分析
對于定性變量,常常根據變量的分類類型來分組,可以采用餅圖和條形圖來描述定性變量的分布,如代碼清單3-4所示。
- 代碼清單3-4 不同菜品在某段時間的銷售量分布情況
- import pandas as pd
- import matplotlib.pyplot as plt
- catering_dish_profit = '../data/catering_dish_profit.xls'# 餐飲數據
- data = pd.read_excel(catering_dish_profit) # 讀取數據,指定“日期”列
- 為索引
- # 繪制餅圖
- x = data['盈利']
- labels = data['菜品名']
- plt.figure(figsize=(8, 6)) # 設置畫布大小
- plt.pie(x,labelslabels=labels) # 繪制餅圖
- plt.rcParams['font.sans-serif'] = 'SimHei'
- plt.title('菜品銷售量分布(餅圖)') # 設置標題
- plt.axis('equal')
- plt.show()
- # 繪制條形圖
- x = data['菜品名']
- y = data['盈利']
- plt.figure(figsize=(8, 4)) # 設置畫布大小
- plt.bar(x,y)
- plt.rcParams['font.sans-serif'] = 'SimHei'
- plt.xlabel('菜品') # 設置x軸標題
- plt.ylabel('銷量') # 設置y軸標題
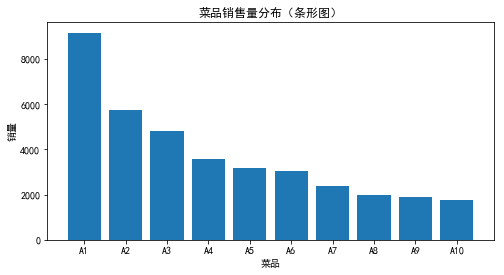
- plt.title('菜品銷售量分布(條形圖)')# 設置標題
- plt.show() # 展示圖片
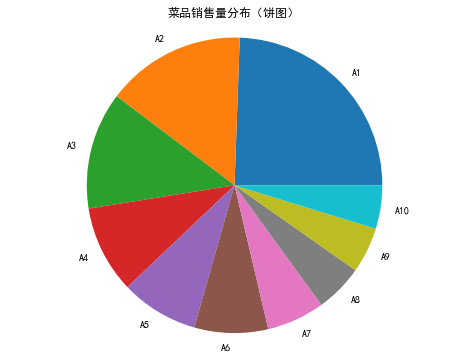
餅圖的每一個扇形部分代表每一類型的所占百分比或頻數,根據定性變量的類型數目將餅圖分成幾個部分,每一部分的大小與每一類型的頻數成正比;條形圖的高度代表每一類型的百分比或頻數,條形圖的寬度沒有意義。
運行代碼清單3-4可得不同菜品在某段時間的銷售量分布圖,如圖3-4和圖3-5所示。
▲圖3‑4 菜品銷售量分布(餅圖)
▲圖3‑5 菜品銷售量分布(條形圖)
關于作者:張良均,資深大數據挖掘與分析專家、模式識別專家、AI技術專家。有10余年大數據挖掘與分析經驗,擅長Python、R、Hadoop、Matlab等技術實現的數據挖掘與分析,對機器學習等AI技術驅動的數據分析也有深入研究。
本文摘編自《Python數據分析與挖掘實戰》(第2版),經出版方授權發布。