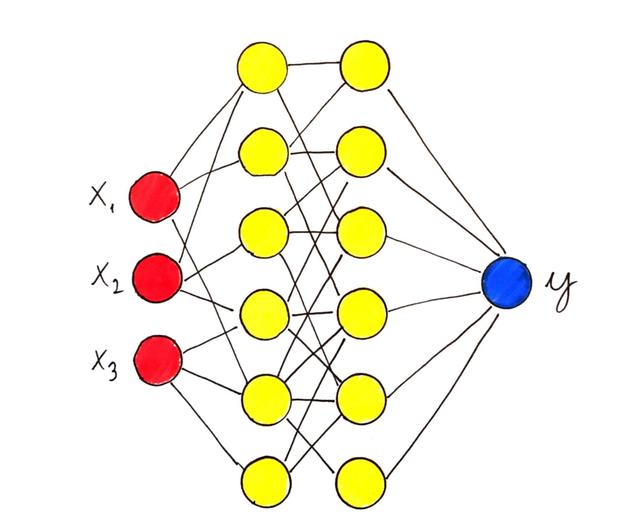
普適逼近定理

眾所周知，神經(jīng)網(wǎng)絡(luò)非常強(qiáng)大，可以將其用于幾乎任何統(tǒng)計學(xué)習(xí)問題，而且效果很好。 但是您是否考慮過為什么會這樣? 為什么在大多數(shù)情況下此方法比許多其他算法更強(qiáng)大?

與機(jī)器學(xué)習(xí)一樣，這有一個精確的數(shù)學(xué)原因。 簡而言之，神經(jīng)網(wǎng)絡(luò)模型描述的功能集非常大。 但是描述一組功能意味著什么? 一組功能如何大? 這些概念乍一看似乎很難理解，但是可以正確定義它們，從而闡明為什么某些算法比其他算法更好的原因。

機(jī)器學(xué)習(xí)作為函數(shù)逼近

讓我們以一個抽象的觀點來闡述什么是機(jī)器學(xué)習(xí)問題。 假設(shè)我們有數(shù)據(jù)集

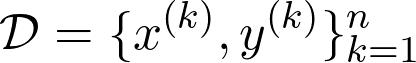
其中x⁽ᵏ⁾是數(shù)據(jù)點，y是與數(shù)據(jù)點相關(guān)的觀測值。 觀測值y⁽ᵏ⁾可以是實數(shù)，甚至可以是概率分布(在分類的情況下)。 任務(wù)只是找到一個函數(shù)f(x)，對于該函數(shù)f(x⁽ᵏ⁾)近似為y⁽ᵏ⁾。

為此，我們預(yù)先修復(fù)了參數(shù)化的功能系列，然后選擇最適合的參數(shù)配置。 例如，線性回歸使用函數(shù)族

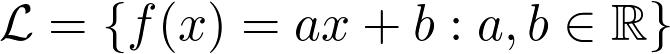
作為參數(shù)的函數(shù)族，以a和b為參數(shù)。

如果我們假設(shè)有一個真實的基礎(chǔ)函數(shù)g(x)描述了x⁽ᵏ⁾和y⁽ᵏ⁾之間的關(guān)系，則該問題可以表述為函數(shù)逼近問題。 這將我們帶入了美麗的近似理論技術(shù)領(lǐng)域。

近似理論入門

可能您一生中多次遇到指數(shù)函數(shù)。 它的定義是

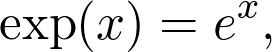
其中e是著名的歐拉數(shù)。 這是一個超越函數(shù)，基本上意味著您無法通過有限的多次加法和乘法來計算其值。 但是，當(dāng)您將其放入計算器時，您仍然會獲得價值。 該值僅是一個近似值，盡管對于我們的目的通常是足夠的。 實際上，我們有

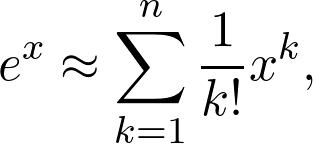
這是一個多項式，因此可以顯式計算其值。 n越大，近似值越接近真實值。

逼近理論的中心問題是為這些問題提供數(shù)學(xué)框架。 如果您有任何函數(shù)g(x)以及從計算方面更易于處理的函數(shù)族，那么您的目標(biāo)就是找到一個與g足夠接近的"簡單"函數(shù)。 本質(zhì)上，近似理論搜索三個核心問題的答案。

• 什么是"足夠接近"?
• 我可以(或應(yīng)該)使用哪個函數(shù)系列來近似?
• 從給定的近似函數(shù)族中，哪一個確切的函數(shù)最適合?

別擔(dān)心這些聽起來是否有點抽象，因為接下來我們將研究神經(jīng)網(wǎng)絡(luò)的特殊情況。

神經(jīng)網(wǎng)絡(luò)作為函數(shù)逼近器

因此，讓我們重申這個問題。 我們有一個函數(shù)g(x)，它描述數(shù)據(jù)和觀測值之間的關(guān)系。 這不是確切已知的，僅對于某些值

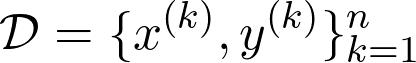
其中g(shù)(x⁽ᵏ⁾)=y⁽ᵏ⁾。 我們的工作是找到一個f(x)

• 從數(shù)據(jù)中概括知識
• 并且在計算上可行。

如果我們假設(shè)所有數(shù)據(jù)點都在子集X中，則

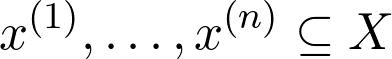
持有，我們想要一個數(shù)量最高準(zhǔn)則的函數(shù)

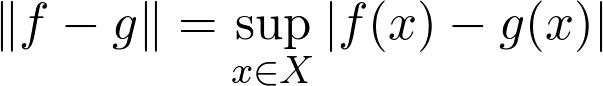
盡可能小。 您可以通過繪制這些函數(shù)，為圖形包圍的區(qū)域著色并計算沿y軸的最大擴(kuò)展區(qū)域來想象這個數(shù)量。

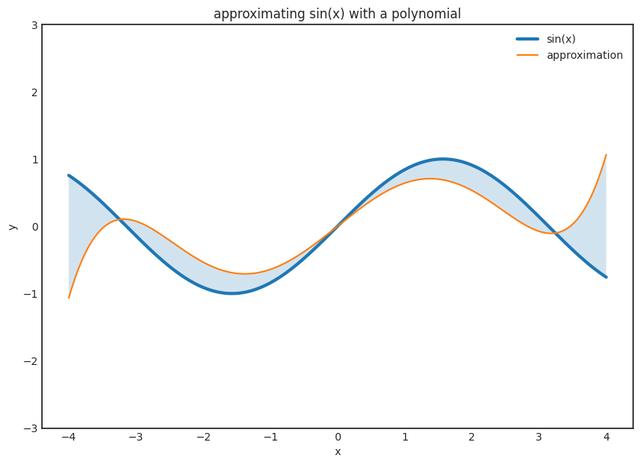
即使我們不能評估g(x)的任意值，我們也應(yīng)該始終在更廣泛的意義上接近它，而不是要求f(x)僅適合已知數(shù)據(jù)點xₖ。

因此，給出了問題。 問題是，我們應(yīng)該使用哪一組函數(shù)進(jìn)行近似?

具有單個隱藏層的神經(jīng)網(wǎng)絡(luò)

從數(shù)學(xué)上講，具有單個隱藏層的神經(jīng)網(wǎng)絡(luò)定義為

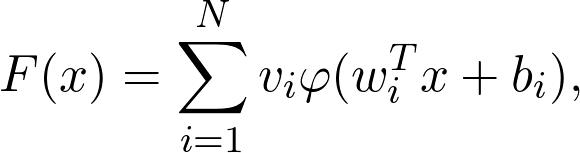
其中φ是非線性函數(shù)(稱為激活函數(shù))，例如S型函數(shù)

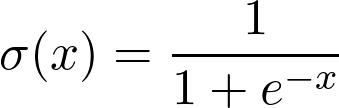
和

值x對應(yīng)于數(shù)據(jù)，而wᵢ，bᵢ和vᵢ是參數(shù)。 是功能家族

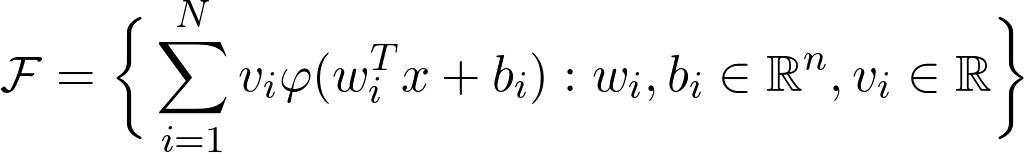
足以近似任何合理的功能? 答案是肯定的!

普適逼近定理

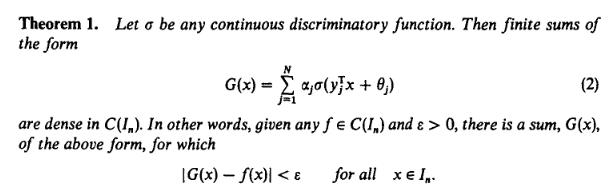
• > The universal approximation theorem in its full glory :) Source: Cybenko, G. (1989) "Approximations by superpositions of sigmoidal functions", Mathematics of Control, Signals, and Systems, 2(4), 303–314.

1989年的一個著名結(jié)果被稱為通用逼近定理，該結(jié)論指出，只要激活函數(shù)像S形函數(shù)且被逼近的函數(shù)是連續(xù)的，具有單個隱藏層的神經(jīng)網(wǎng)絡(luò)就可以根據(jù)需要精確地對其進(jìn)行逼近。 (或使用機(jī)器學(xué)習(xí)術(shù)語進(jìn)行學(xué)習(xí)。)

如果確切的定理似乎很困難，請不要擔(dān)心，我將詳細(xì)解釋整個過程。 (實際上，我故意跳過了稠密之類的概念，以使說明更清晰，盡管不夠精確。)

步驟1。 假設(shè)要學(xué)習(xí)的函數(shù)是g(x)，它是連續(xù)的。 讓我們固定一個小的ε并在函數(shù)周圍繪制一個ε寬的條紋。 ε越小，結(jié)果越好。

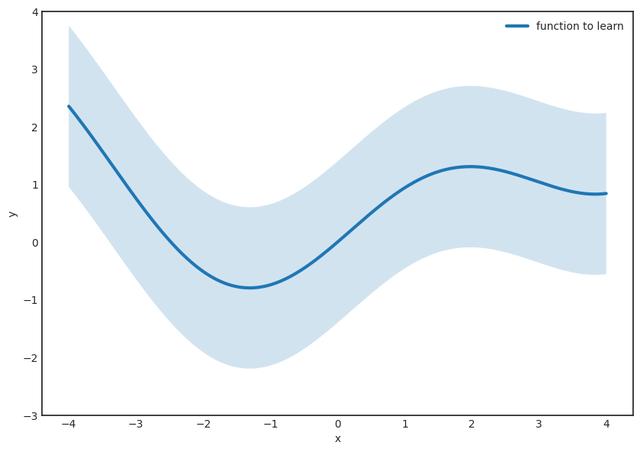
第二步。 (最困難的部分。)找到表格的功能

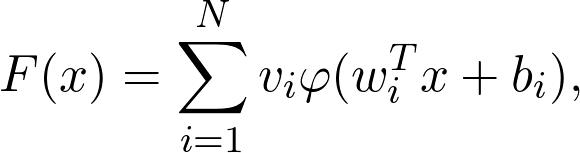
完全在條紋內(nèi) 該定理保證了這樣的F(x)的存在，因此這個函數(shù)族被稱為通用逼近器。 這是神經(jīng)網(wǎng)絡(luò)的真棒，賦予它們真正的力量。

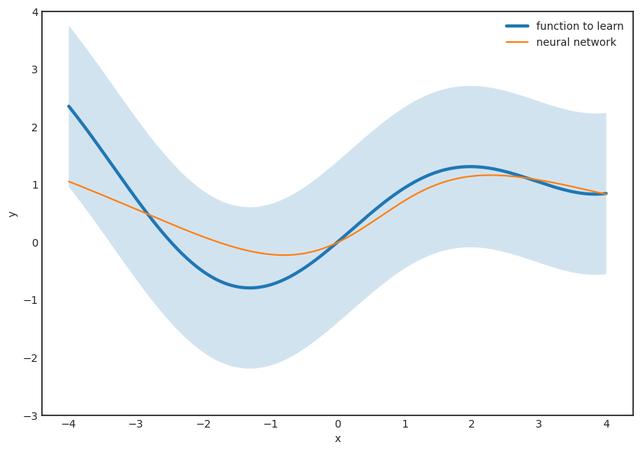
但是，有幾個警告。 例如，該定理沒有說出N，也就是隱藏層中神經(jīng)元的數(shù)量。 對于較小的ε，它可能非常大，從計算角度來看這是不利的。 我們希望盡快計算預(yù)測，而計算100億項之和絕對不好玩。

第二個問題是，即使該定理保證了一個良好的逼近函數(shù)的存在，也沒有告訴我們?nèi)绾握业剿?盡管這可能令人驚訝，但這在數(shù)學(xué)中是非常典型的。 我們有非常強(qiáng)大的工具來推斷某些對象的存在，而又不能顯式構(gòu)造它們。 (有一所稱為建構(gòu)主義的數(shù)學(xué)學(xué)校，它拒絕純粹的存在性證明，例如通用逼近定理的原始證明。但是，這個問題根深蒂固。如果不接受非構(gòu)造性證明，我們甚至無法談?wù)? 無限集上的函數(shù)。)

但是，最大的問題是，在實踐中，我們永遠(yuǎn)不會完全了解底層功能，而只會知道所觀察到的內(nèi)容：

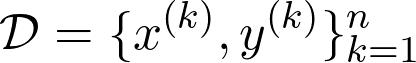
有無數(shù)種可能的配置可以很好地適合我們的數(shù)據(jù)。 它們中的大多數(shù)可怕地概括為新數(shù)據(jù)。 您肯定知道這種現(xiàn)象：這是可怕的過度擬合。

擁有權(quán)利的同時也被賦予了重大的責(zé)任

所以，這是東西。 如果您有N個觀測值，則可以找到一個非常適合您的觀測值的N-1階多項式。 這沒什么大不了的，您甚至可以使用Lagrange插值明確地寫下該多項式。 但是，它不會推廣到任何新數(shù)據(jù)，實際上會很糟糕。 下圖展示了當(dāng)我們嘗試將大多項式擬合到一個小的數(shù)據(jù)集時會發(fā)生什么。

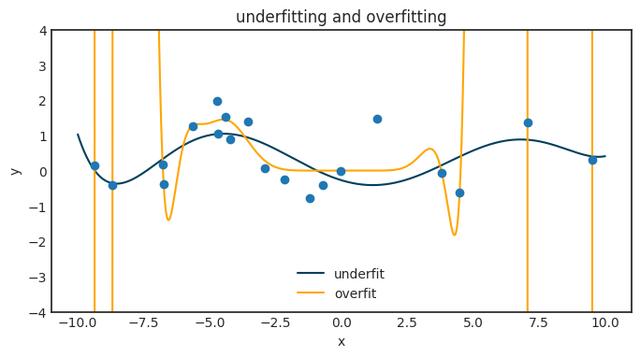
神經(jīng)網(wǎng)絡(luò)也有同樣的現(xiàn)象。 這是一個巨大的問題，而通用逼近定理給我們關(guān)于如何克服這一問題的絕對零提示。

通常，功能族的表現(xiàn)力越高，就越容易過度擬合。 擁有權(quán)利的同時也被賦予了重大的責(zé)任。 這稱為偏差方差折衷。 對于神經(jīng)網(wǎng)絡(luò)，從權(quán)重的L1正則化到下降層，有很多方法可以緩解這種情況。 但是，由于神經(jīng)網(wǎng)絡(luò)具有如此高的表現(xiàn)力，因此這個問題始終在后臺隱約可見，需要不斷關(guān)注。

超越萬能逼近定理

正如我已經(jīng)提到的，該定理沒有提供任何工具來為我們的神經(jīng)網(wǎng)絡(luò)找到參數(shù)配置。 從實際的角度來看，這幾乎與通用逼近性質(zhì)一樣重要。 幾十年來，神經(jīng)網(wǎng)絡(luò)一直不受歡迎，因為缺乏一種計算有效的方法來使它們適合數(shù)據(jù)。 有兩項重要的進(jìn)步，使它們的使用成為可能：反向傳播和通用GPU-s。 有了這兩個工具，訓(xùn)練龐大的神經(jīng)網(wǎng)絡(luò)變得輕而易舉。 您可以使用筆記本訓(xùn)練最先進(jìn)的模型，甚至不費(fèi)吹灰之力。 自從通用逼近定理以來，我們已經(jīng)走到現(xiàn)在!

通常，這是標(biāo)準(zhǔn)深度學(xué)習(xí)課程的起點。 由于其數(shù)學(xué)上的復(fù)雜性，因此未涵蓋神經(jīng)網(wǎng)絡(luò)的理論基礎(chǔ)。 但是，通用逼近定理(及其證明中使用的工具)對神經(jīng)網(wǎng)絡(luò)為何如此強(qiáng)大提供了非常深入的了解，甚至為工程新穎的體系結(jié)構(gòu)奠定了基礎(chǔ)。 畢竟，誰說過我們只能將S型和線性函數(shù)結(jié)合起來?