Google的面試題長啥樣?看完被吊打!
作為一名Google的工程師和面試官,今天是我第二次發文分享科技公司面試建議了。這里先聲明:本文僅代表我個人的觀察、意見和建議。請勿當作來自Google或Alphabet的官方建議或聲明。
下面這個問題,是我面試生涯中第一個問題;也是第一個被泄漏出來,以及第一個被禁掉的問題。我喜歡這個問題,因為它有以下優點:
問題很容易表述清楚,也容易理解。
這個問題有多個解。每個解都需要不同程度的算法和數據結構知識。而且,還需要一點點遠見。
每個解都可以簡單幾行代碼實現,非常適合有時間限制的面試。
如果你是學生,或者求職者,我希望你通過本文能夠了解到,面試問題一般會是怎么樣的。如果你也是面試官,我很樂意分享自己在面試中的風格和想法,如何更好地傳達信息、征求意見。
注意,我將使用Python寫代碼;我喜歡Python因為它易學,簡潔,而且有海量的標準庫。我遇到的很多面試者也很喜歡,盡管我們推行“不限定語言”的政策,我面試90%的人都用Python。而且,我用的Python 3因為,拜托,這都2018年了。
問題
把你的手機撥號頁想象成一個棋盤。棋子走只能走“L”形狀,橫著兩步,豎著一步;或者豎著兩步,橫著一步。

現在,假設你撥號只能像棋子一樣走“L”形狀。每走完一個“L”形撥一次號,起始位置也算撥號一次。問題:從某點開始,在N步內,你可以撥到多少不同的數字?
討論
每次面試,我基本都會分成兩個部分:首先我們找出算法方案,然后讓面試者在代碼中實現。我說“我們找出算法方案”,因為這個過程我不是沉默的獨裁者。在這樣高壓下,設計并實現一種算法,45分鐘時間并不算充足。

當聽完面試官的問題,你應該做什么?切記不要立刻就去寫代碼,而是在黑板上試著一步一步去分解問題。分解問題能夠幫助你尋找到規律,特例等等,逐漸在大腦中形成解決方案。比如,你現在從數字6開始走,能走2步,會有如下組合:
- 6–1–8
- 6–1–6
- 6–7–2
- 6–7–6
- 6–0–4
- 6–0–6
一共有6種組合。你可以試著用鉛筆在紙上畫,相信我,有時候動手去解決問題會發生意想不到的事,比你盯著在腦袋里想更神奇。
怎么樣?你腦海里有方案了嗎?
第0階:到達下一步
使用這個問題面試,最讓我驚訝的是,太多人都卡在了計算從某個特定點跳出時,一共有多少種可能,即鄰Neighbors。我的建議是:當你不確定時,先寫個占位符,然后請求面試官能否晚點實現這一部分。
這個問題的復雜性并不在Neighbors的計算;我在意的是你如何計算出總數。所有花費在計算Neighbors上的時間其實都是浪費。
我會接受“讓我們假設有一個函數能給出我Neighbors”。當然,我也可能會讓你后面有時間再去實現這一步,你只需要這樣寫,然后繼續。

而且,如果一個問題的復雜性不在這里,你也可以問我能不能先略過,一般我都是允許的。我倒是不介意面試者不知道問題的復雜性在哪里,尤其剛開始他們還沒有全面了解問題的時候。
至于Neighbors函數,因為數字永遠不變,你可以直接寫一個Map然后返回符合的值。

第1階:遞歸
聰明的你可能注意到了,這個問題可以通過枚舉出所有符合條件的數字,然后計算。這里可以使用遞歸產生這些值:
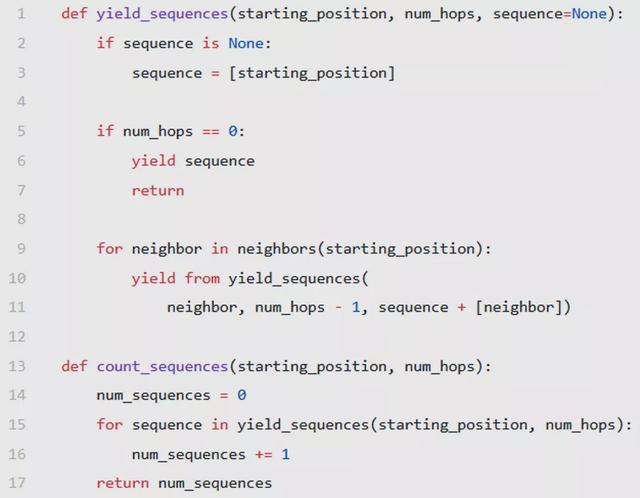
這個方法可以,而且是在面試中最普遍的方法。但是請注意,我們產生了這么多數字卻并沒有使用他們,我們計算完他們的個數后,就再也不去碰了。所以我建議大家遇到這種情況,盡量去想一下看有沒有更好的方案。
第2階:數不數數
怎么在不產生這些數字的情況下計算出個數?可以做到,但需要一點點機智。注意從特定點跳出N次能夠撥到的數字個數,等于從它所有臨近的點跳出N-1次能夠撥到的數字個數的總和。我們可以表達為這樣的遞歸關系:
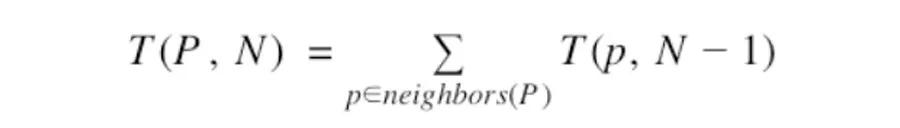
如果你這樣想,就會很直觀了,跳一次時:6有3個neighbors(1,7和0),當跳0次時每個數字本身算一次,因此每次你只能撥到3個數字。
怎么會產生這樣機智的想法?其實,如果你學了遞歸,并且在黑板上好好研究,這一點就會變得顯而易見。這樣你就能繼續去解決這個問題,實際上就這一點就有多種實現方法,下面這個便是面試中最常見的:

就是這樣,結合這個函數計算出neighbors 就可以了。這時候,你就可以捏捏肩膀休息下了,因為到這里,你已經刷掉很多人了。
接下來這個問題我經常問:這個方案的算法理論速度如何?在這個實現中,每次調用count_sequences()都會遞歸地調用count_sequences()至少2次,因為每個數字至少有2個neighbors。這樣會導致runtime成指數增長。
對于跳1次到20次這樣的次數還可以,但是到更大的數字,我們就要碰壁。500次可能就需要整個宇宙的熱量來完成運算。
第3階:記憶
那么,我們能做的更好么?使用上面的方法,并不能。我喜歡這個問題,也是因為他能一層一層帶出大家的智慧,找到更高效的方法。為了找到更好的方法,讓我們看下這個函數是怎么調用的,以count_sequences(6, 4)為例。注意這里用C作為函數名簡化。
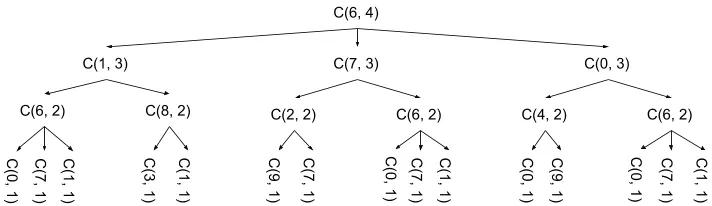
你可能注意到了,C(6, 2)運行了3次,每次都是同樣的運算并返回同樣的值。這里最關鍵的點在于這些重復的運算,每次你使用過他們的值之后,就沒有必要再次計算。
怎么解決這個問題?記憶。我們那些相同的函數調用和結果,而不是讓他們重復。這樣,在后面我們就可以直接給出之前的結果。實現方法如下:

第4階:動態設計
如果你再看看前面的遞歸關系,就會發現遞歸記憶的方案也有一點局限性:
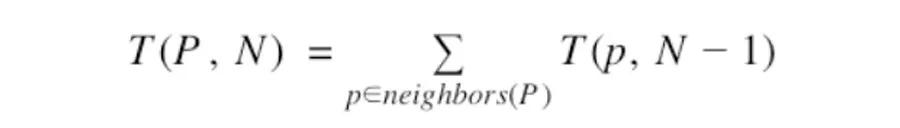
注意跳N次的結果僅僅取決于跳N-1次后調用的結果。同時,緩存中包含著每個次數的所有結果。我之所以說這是個小局限,因為確實不會造成真的問題,當跳的次數增長時,緩存也只是線性增長。但是,畢竟,這還是不夠高效。
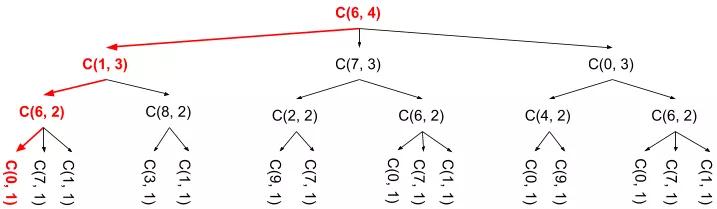

這個版本比前面遞歸版好在哪里?其實并沒有好很多,但是這個不是遞歸的,因此即使處理超大數據也很難崩潰。其次,它使用的是常量內存;最后,它仍舊是線性增長,即便處理200000次跳也只用不到20秒。
評估
到這里,基本就算完了。設計并實現一個線性時的、產量內存的方案,在面試中是非常好的結果。在我的面試中,如果有面試者寫出動態編程設計,我通常會給他一個極高的評價:excellent!
當評估算法和數據結構的時候,我經常會說:面試者對問題認識清晰,并且考慮到各方面的可能,當指出不足時他也能迅速改進并提高;最終,實現了一個不錯的解決方案。
當評估代碼的時候,我最理想的說法是:面試者迅速并精確地把想法轉化為了代碼;代碼結構嚴謹,容易閱讀。所有特殊情況都有概括,并且認真檢查測試了代碼,確保了沒有Bug。
總結
我知道,這個面試問題看上去似乎有點嚇人,尤其整個解釋下來非常繁瑣。但本文的目的和面試中完全不一樣。最后,一點面試相關的技巧,以及一些好的習慣,分享給大家:
- 一定要手動來,從最小的問題開始解決。
- 當你的程序在做無用的運算時,一定要注意去優化。減少不必要的運算能夠讓你的解決方案更加簡潔,說不定能因此發現更高效的方案。
- 了解你的遞歸函數。在實際生產中,遞歸常常很容易出問題,但它仍舊是非常強大的算法設計和策略。遞歸方案也總是有優化和提高的余地。
- 要常常去尋找記憶的機會。如果你的函數是目的性的,并且會多次調用相同的值,那么就試著去存儲起來。