測(cè)試分布式系統(tǒng)的線性一致性
最近看到一篇文章 ,寫得非常好,在征得作者 Anish 同意的情況下,決定將其翻譯成中文。但為了更好理解,一些地方并不會(huì)逐字翻譯,也會(huì)稍作調(diào)整。
正確實(shí)現(xiàn)一個(gè)分布式系統(tǒng)是非常有挑戰(zhàn)的一件事情,因?yàn)樾枰芎玫奶幚聿l(fā)和失敗這些問題。網(wǎng)絡(luò)包可能被延遲,重復(fù),亂序或者丟棄,機(jī)器可能在任何時(shí)候宕機(jī)。即使一些設(shè)計(jì)被論文證明是正確的,也仍然很難再實(shí)現(xiàn)中避免 bug。
除非我們使用形式方法,不然,即使我們假設(shè)實(shí)現(xiàn)是正確的,我們也需要去測(cè)試系統(tǒng)。測(cè)試分布式系統(tǒng)也是一件非常有挑戰(zhàn)的事情。并發(fā)和不確定性使得我們?cè)跍y(cè)試的時(shí)候非常難抓住 bug,尤其是在一些極端情況下面才會(huì)出現(xiàn)的 bug,譬如同時(shí)機(jī)器宕機(jī)或者極端網(wǎng)絡(luò)延遲。
正確性
在討論測(cè)試分布式系統(tǒng)的正確性之前,我們首先定義下什么是 “正確性”。即使對(duì)于一些簡(jiǎn)單的系統(tǒng),要完全的確定系統(tǒng)符合預(yù)期也是一件相當(dāng)復(fù)雜的事情。
考慮一個(gè)簡(jiǎn)單的 key-value 系統(tǒng),譬如 etcd,支持兩個(gè)操作:Put(key, value) 和 Get(key),首先,我們需要考慮它在順序情況下面的行為。
順序規(guī)范
通常對(duì)于一個(gè) key-value store,我們對(duì)于它在順序操作下面的行為都能有一個(gè)直觀的認(rèn)識(shí):Get 操作如果在 Put 的后面,那么一定能得到 Put 的結(jié)果。譬如,如果 Put("x", "y") ,那么后面的 Get("x") 就能得到 "y",如果得到了 "z",那么這就是不對(duì)的。
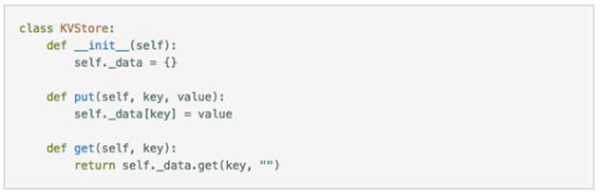
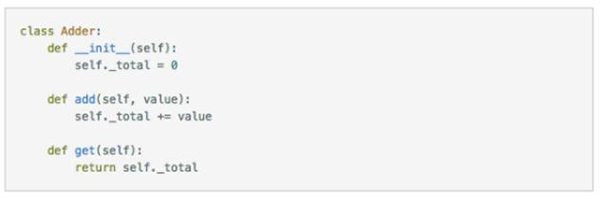
我們使用 Python 定義一個(gè)簡(jiǎn)單的 key-value store:
上面的代碼比較簡(jiǎn)單,但包含了足夠的信息,包括初始狀態(tài)是怎樣的,內(nèi)部狀態(tài)是如何被操作的結(jié)果改變的,從 key-value store 里面操作返回的結(jié)果是怎樣的。這里需要留意下 Get() 對(duì)于不存在的 key 的處理,會(huì)返回一個(gè) empty string。
線性一致性
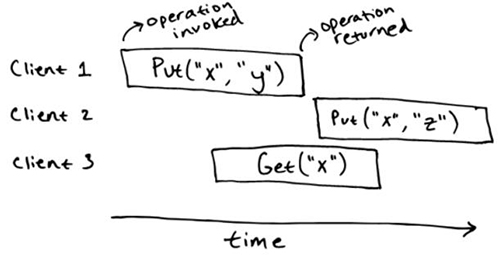
接下來,我們來考慮我們的 key-value store 在并發(fā)下面會(huì)有怎樣的行為。需要注意順序規(guī)范并沒有指明在并發(fā)操作下面會(huì)發(fā)生什么。譬如,順序規(guī)范并沒有說 key-value store 在下面這個(gè)場(chǎng)景下可以允許的操作。
我們并不能立刻知道 Get("x") 這個(gè)操作會(huì)允許返回怎樣的結(jié)果。直覺上,我們可以說 Get("x")是跟 Put("x", "y") 和 Put("x", "z") 一起執(zhí)行的,所以它能可能返回一個(gè)值,甚至也可能返回 ""。 如果有另一個(gè) Get("x") 的操作在更后面執(zhí)行,我們可以說這個(gè)一定能返回 "z",因?yàn)樗?**一次寫入的值,而且那個(gè)時(shí)候并沒有其他的并發(fā)寫入。
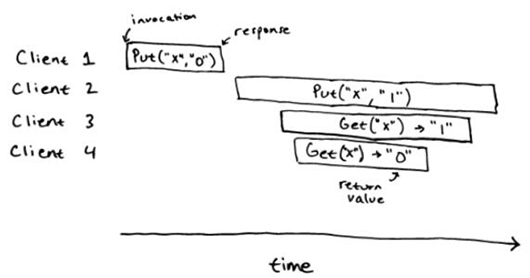
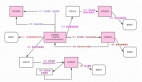
對(duì)于一個(gè)基于順序規(guī)范的并發(fā)操作來說,我們會(huì)用一個(gè)一致性模型,也就是線性一致性來說明它的正確性。在一個(gè)線性一致性的系統(tǒng)里面,任何操作都可能在調(diào)用或者返回之間原子和瞬間執(zhí)行。除了線性一致性,還有一些其他一致性的模型,但多數(shù)分布式系統(tǒng)都提供了線性一致性的操作:線性一致性是一個(gè)強(qiáng)的一致性模型,并且基于線性一致性系統(tǒng),很容易去構(gòu)建其他的系統(tǒng)。考慮到如下對(duì) key-value store 操作的歷史例子:
這個(gè)歷史是一個(gè)線性的。在下面圖片的藍(lán)色地方,我們現(xiàn)實(shí)的標(biāo)明了線性一致的點(diǎn)。這個(gè)順序歷史 Put("x", "0"), Get("x") -> "0", Put("x", "1"), Get("x") -> "1",對(duì)于順序規(guī)范來說就是一個(gè)正確的歷史。
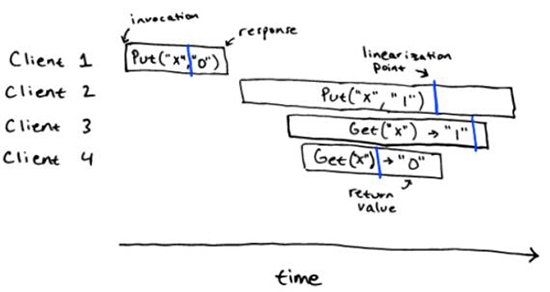
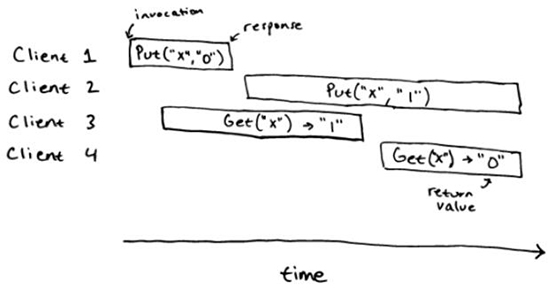
對(duì)應(yīng)的,下面的歷史就不是線性一致的。
對(duì)于順序規(guī)范來說,這個(gè)歷史并不是線性一致的:我們并不能在這個(gè)歷史的操作里面指定出線性一致的點(diǎn)。我們可以畫出 client 1,2 和 3 的,但我們并不能畫出 client 4 的,因?yàn)檫@明顯是一個(gè)過期的值。類似的,我們可以畫出 client 1,2 和 4 的,那么 client 2 的操作一定會(huì)在 4 的操作開始的后面,但這樣我們就不能處理 client 3,它只可能合法的返回 "" 或者 "0"。
測(cè)試
有了一個(gè)正確性的定義,我們就可以考慮如何去測(cè)試分布式系統(tǒng)了。通常的做法就是對(duì)于正確的操作,不停的進(jìn)行隨機(jī)的錯(cuò)誤注入,類似機(jī)器宕機(jī),網(wǎng)絡(luò)隔離等。我們甚至能模擬整個(gè)網(wǎng)絡(luò),這樣我們就能做長(zhǎng)時(shí)間的網(wǎng)絡(luò)延遲等。因?yàn)闇y(cè)試時(shí)隨機(jī)的,我們需要跑很多次從而確定一個(gè)系統(tǒng)的實(shí)現(xiàn)是正確的。
專門測(cè)試
我們實(shí)際如何做正確操作的測(cè)試呢?在最簡(jiǎn)單的軟件里面,我們可以使用輸入輸出測(cè)試,譬如 assert(expected_output == f(input)),我們也可以在分布式系統(tǒng)上面使用一個(gè)類似的方法,譬如,對(duì)于 key-value store,當(dāng)多個(gè) client 開始執(zhí)行操作的時(shí)候,我們可以有如下的測(cè)試:
如果測(cè)試掛掉了,那么這個(gè)系統(tǒng)一定不是線性一致性的,當(dāng)然,這個(gè)測(cè)試并不是很完備,因?yàn)橛锌赡懿皇蔷€性一致的系統(tǒng)也可能通過這個(gè)測(cè)試。
線性一致性
一個(gè)更好的辦法就是并發(fā)的客戶端完全跑隨機(jī)的操作。譬如,循環(huán)的去調(diào)用 kvstore.put(rand(), rand()) 和 kvstore.get(rand()),有可能會(huì)只用很少的 key 去增大沖突的概率。但在這種情況下,我們?nèi)绾味x什么是正確的操作呢?在上面的簡(jiǎn)單的測(cè)試?yán)锩妫驗(yàn)槊總€(gè) client 都操作的是一個(gè)獨(dú)立的 key,所以我們可以非常明確的知道輸出結(jié)果。
但是 clients 并發(fā)的操作同一堆 keys,事情就變得復(fù)雜了。我們并不能預(yù)知每個(gè)操作的返回值因?yàn)檫@并沒樣一個(gè)唯一的答案。但我們可以用另一個(gè)辦法:我們可以記錄整個(gè)操作的歷史,然后去驗(yàn)證這個(gè)操作歷史是線性一致的。
線性一致性驗(yàn)證
一個(gè)線性一致性驗(yàn)證器會(huì)使用一個(gè)順序規(guī)范和一個(gè)并發(fā)操作的歷史,然后執(zhí)行一個(gè)判定程序去檢查這個(gè)歷史在規(guī)范下面是否線性一致。
NP 完備
但不幸的是,線性一致性驗(yàn)證是 NP 完備的。這個(gè)證明非常簡(jiǎn)單:我們能說明線性一致性驗(yàn)證是 NP 問題,并且也能展示一個(gè) NP 困難問題能被簡(jiǎn)化成線性一致性驗(yàn)證。明顯的,線性一致性驗(yàn)證是 NP 問題,譬如,所有操作的線性一致性點(diǎn),根據(jù)相關(guān)的順序規(guī)范,我們可以在多項(xiàng)式時(shí)間里驗(yàn)證。
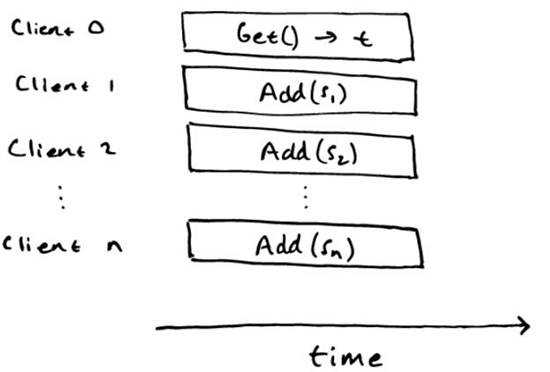
為了說明線性一致性驗(yàn)證是 NP 困難的,我們可以將子集合問題簡(jiǎn)化成線性一致性驗(yàn)證。對(duì)于子集合問題,我們給出非負(fù)數(shù)的集合 S={s1,s2,…,sn} 和目標(biāo)結(jié)果 t,然后我們必須確定是否存在一個(gè)子集 S 的合等于 t。我們可以將這個(gè)問題簡(jiǎn)化成如下的線性一致性驗(yàn)證。考慮順序規(guī)范:
以及歷史:
只有在子集合問題的答案是 “yes” 的時(shí)候,歷史才是線性的。如果歷史是線性的,那么我們認(rèn)為對(duì)于任何的 Add(s_i) 操作,在 Get() 操作之前都有線性一致性點(diǎn),這個(gè)就對(duì)應(yīng)了在子集里面 Si,它的合是 t。如果這個(gè)集合里面有一個(gè)子集的合是 t,我們就能構(gòu)造一個(gè)線性化,它有在 Get 操作發(fā)生之前,對(duì)應(yīng)子集 Si 的 Add(s_i) 的操作,也有在 Get() 操作之后其余的操作。
PS:這個(gè)章節(jié)我大概知道啥意思,但沒找到更好的表述來翻譯,也就湊合著了。后面再看 paper 來深入了解吧。
實(shí)現(xiàn)
即使線性一致性驗(yàn)證是 NP 完全的,在實(shí)際中,它仍然能在一些小的歷史上面很好的工作。線性一致性驗(yàn)證器的實(shí)現(xiàn)會(huì)用一個(gè)可執(zhí)行的規(guī)范,加上一個(gè)歷史,執(zhí)行一個(gè)搜索過程去構(gòu)造一個(gè)線性化,并使用一些技巧來限制減少搜索的空間。
在 Jepsen 里面,有一個(gè)一致性驗(yàn)證工具 Knossos,但不幸的是,在測(cè)試一些分布式 key-value store 的時(shí)候,Knossos 并不能很好的工作,它可能只能適用于一些少的并發(fā) clients,以及只有幾百的事件的歷史。但在一些測(cè)試?yán)锩妫泻芏嗟? clients,以及會(huì)生成更多的歷史事件。為了解決 Knossos 的問題,作者開發(fā)了 Procupine,一個(gè)用 Go 寫的更快的線性一致性驗(yàn)證工具。Porcupine 使用一個(gè)用 Go 開發(fā)的執(zhí)行規(guī)范去驗(yàn)證歷史是否是線性的。根據(jù)實(shí)際測(cè)試的情況,Porcupine 比 Knossos 快很多倍。
效果
在測(cè)試分布式系統(tǒng)的線性一致性的時(shí)候,使用錯(cuò)誤注入是一個(gè)很有效的手段。
作為對(duì)比,在使用專門的測(cè)試用 Porcupine 測(cè)試 key-value store 的時(shí)候,作者使用了這兩種方式。作者在實(shí)現(xiàn)它自己的 key-value store 的時(shí)候引入不同的設(shè)計(jì)錯(cuò)誤,譬如在修改之后會(huì)出現(xiàn)過期讀,來看這些測(cè)試是否會(huì)掛掉。專門測(cè)試會(huì)捕捉到很多 bugs,但并沒有能力去捕捉到更多的狡猾的 bugs。相對(duì)而言,作者現(xiàn)在還沒找到一個(gè)正確性的 bug 是線性一致性測(cè)試不能抓住的。
- 形式方法能夠保證一個(gè)分布式系統(tǒng)的正確性。例如,UM PLSE 研究小組最近使用 Coq proof assistnt 來驗(yàn)證了 Raft 一致性協(xié)議。但不幸的的是,驗(yàn)證需要特定的知識(shí),另外驗(yàn)證實(shí)際的系統(tǒng)需要做大量的工作。沒準(zhǔn)有一天,驗(yàn)證能被用在實(shí)際系統(tǒng)上面,但現(xiàn)在,主要還是測(cè)試,而不是驗(yàn)證。
- 理論上,所有的生產(chǎn)系統(tǒng)都會(huì)有一個(gè)形式規(guī)范,而且一些系統(tǒng)也已經(jīng)有了,譬如 Raft 就有一個(gè)用 TLA+ 寫的形式規(guī)范。但不幸的是,大部分的系統(tǒng)是沒有的。
【本文是51CTO專欄作者“PingCAP”的原創(chuàng)文章,轉(zhuǎn)載請(qǐng)聯(lián)系作者本人獲取授權(quán)】