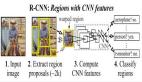
深度神經(jīng)網(wǎng)絡的數(shù)學基礎,對你來說會不會太難?
深度前饋網(wǎng)絡
我們從統(tǒng)計學出發(fā),先很自然地定義一個函數(shù) f,而數(shù)據(jù)樣本由⟨Xi,f(Xi)⟩給出,其中 Xi 為典型的高維向量,f(Xi) 可取值為 {0,1} 或一個實數(shù)。我們的目標是找到一個最接近于描述給定數(shù)據(jù)的函數(shù) f∗(不過擬合的情況下),因此其才能進行精準的預測。
在深度學習之中,總體上來說就是參數(shù)統(tǒng)計的一個子集,即有一族函數(shù) f(X;θ),其中 X 為輸入數(shù)據(jù),θ為參數(shù)(典型的高階矩陣)。而目標則是尋找一組最優(yōu)參數(shù)θ∗,使得 f(X;θ∗) 最合適于描述給定的數(shù)據(jù)。
在前饋神經(jīng)網(wǎng)絡中,θ就是神經(jīng)網(wǎng)絡,而該網(wǎng)絡由 d 個函數(shù)組成:
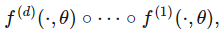
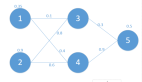
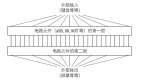
大部分神經(jīng)網(wǎng)絡都是高維的,因此其也可以通過以下結(jié)構(gòu)圖表達:
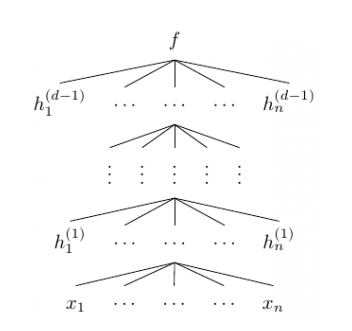
其中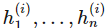 是向量值函數(shù) f(i) 的分量,也即第 i 層神經(jīng)網(wǎng)絡的分量,每一個
是向量值函數(shù) f(i) 的分量,也即第 i 層神經(jīng)網(wǎng)絡的分量,每一個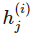 是
是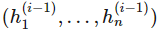 的函數(shù)。在上面的結(jié)構(gòu)圖中,每一層函數(shù) f(i) 的分量數(shù)也稱為層級 i 的寬度,層級間的寬度可能是不一樣的。我們稱神經(jīng)網(wǎng)絡的層級數(shù) d 為網(wǎng)絡的深度。重要的是,第 d 層的神經(jīng)網(wǎng)絡和前面的網(wǎng)絡是不一樣的,其為輸出層,在上面的結(jié)構(gòu)圖中,輸出層的寬度為 1,即 f=f(d) 為一個標量值。通常統(tǒng)計學家最喜歡的是線性函數(shù),但如果我們規(guī)定神經(jīng)網(wǎng)絡中的函數(shù) f(i) 為一個線性函數(shù),那么總體的組合函數(shù) f 也只能是一個線性函數(shù),也樣就完全不能擬合高維復雜數(shù)據(jù)。因此我們通常激活函數(shù)使用的是非線性函數(shù)。
的函數(shù)。在上面的結(jié)構(gòu)圖中,每一層函數(shù) f(i) 的分量數(shù)也稱為層級 i 的寬度,層級間的寬度可能是不一樣的。我們稱神經(jīng)網(wǎng)絡的層級數(shù) d 為網(wǎng)絡的深度。重要的是,第 d 層的神經(jīng)網(wǎng)絡和前面的網(wǎng)絡是不一樣的,其為輸出層,在上面的結(jié)構(gòu)圖中,輸出層的寬度為 1,即 f=f(d) 為一個標量值。通常統(tǒng)計學家最喜歡的是線性函數(shù),但如果我們規(guī)定神經(jīng)網(wǎng)絡中的函數(shù) f(i) 為一個線性函數(shù),那么總體的組合函數(shù) f 也只能是一個線性函數(shù),也樣就完全不能擬合高維復雜數(shù)據(jù)。因此我們通常激活函數(shù)使用的是非線性函數(shù)。
最常用的激活函數(shù)來自神經(jīng)科學模型的啟發(fā),即每一個細胞接收到多種信號,但神經(jīng)突觸基于輸入只能選擇激活或不激活一個特定的電位。因為輸入可以表征為 。
。
對于一些非線性函數(shù) g,由樣本激勵的函數(shù)可以定義為: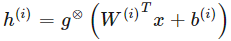
其中 g⊗ 定義了以線性函數(shù)為自變量的一個非線性函數(shù)。
通常我們希望函數(shù) g 為非線性函數(shù),并且還需要它能很方便地求導。因此我們一般使用 ReLU(線性整流單元)函數(shù) g(z)=max(0,z)。其它類型的激活函數(shù) g 還包括 logistic 函數(shù):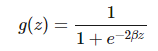 和雙曲正切函數(shù):
和雙曲正切函數(shù):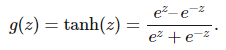 。
。
這兩種激活函數(shù)相對 ReLU 的優(yōu)點,即它們都是有界函數(shù)。
正如前面所說的,最后的輸出層和前面的層級都不一樣。首先它通常是標量值,其次它通常會有一些統(tǒng)計學解釋: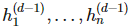 。
。
通常可以看作經(jīng)典統(tǒng)計學模型的參數(shù),且 d-1 層的輸出構(gòu)成了輸出層激活函數(shù)的輸入。輸出層激活函數(shù)可以使用線性函數(shù)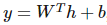 。
。
該線性函數(shù)將輸出作為高斯分布的條件均值。其它也可以使用 σ(wTh+b),其中σ代表 sigmoid 函數(shù),即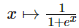
該 sigmoid 函數(shù)將輸出視為 P(y)為 exp(yz) 的伯努利試驗,其中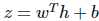 更廣義的 soft-max 函數(shù)可以給定為:
更廣義的 soft-max 函數(shù)可以給定為:
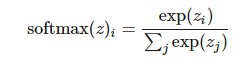
其中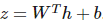 。
。
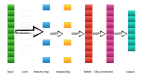
現(xiàn)在,z 的分量和可能的輸出值相對應,softmax(z)i 代表輸出值 i 的概率。例如輸入圖像到神經(jīng)網(wǎng)絡,而輸出(softmax(z)1,softmax(z)2,softmax(z)1)則可以解釋為不同類別(如貓、狗、狼)的概率。
卷積網(wǎng)絡
卷積網(wǎng)絡是一種帶有線性算符的神經(jīng)網(wǎng)絡,即采用一些隱藏的幾何矩陣作為局部卷積算符。例如,第 k 層神經(jīng)網(wǎng)絡可以用 m*m 階矩陣表達:
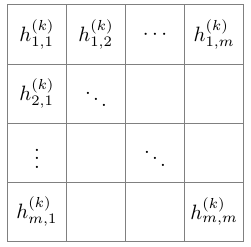
我們定義 k+1 層的函數(shù)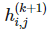 可以由 2*2 矩陣在前一層神經(jīng)網(wǎng)絡執(zhí)行卷積而得出,然后再應用非線性函數(shù) g:
可以由 2*2 矩陣在前一層神經(jīng)網(wǎng)絡執(zhí)行卷積而得出,然后再應用非線性函數(shù) g:
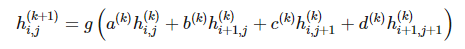 。
。
參數(shù) a(k)、b(k)、c(k) 和 d(k) 只取決于不同層級濾波器的設定,而不取決于特定的元素 i,j。雖然該約束條件在廣義定義下并不必要,但在一些如機器視覺之類的應用上還是很合理的。除了有利于參數(shù)的共享,這種類型的網(wǎng)絡因為函數(shù) h 的定義而自然呈現(xiàn)出一種稀疏的優(yōu)良特征。
卷積神經(jīng)網(wǎng)絡中的另一個通用的部分是池化操作。在執(zhí)行完卷積并在矩陣索引函數(shù) 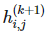 上應用了 g 之后,我們可以用周圍函數(shù)的均值或最大值替代當前的函數(shù)。即設定:
上應用了 g 之后,我們可以用周圍函數(shù)的均值或最大值替代當前的函數(shù)。即設定:
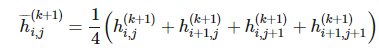
這一技術(shù)同時可以應用到降維操作中。
模型和優(yōu)化
下面我們需要了解如何求得神經(jīng)網(wǎng)絡參數(shù),即到底我們該采取什么樣的 θ 和怎么樣評估θ。對此,我們通常使用概率建模的方法。即神經(jīng)網(wǎng)絡的參數(shù)θ決定了一個概率分布 P(θ),而我們希望求得 θ 而使條件概率 Pθ(y|x) 達到極大值。即等價于極小化函數(shù):
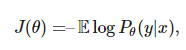
其中可以用期望取代對數(shù)似然函數(shù)。例如,如果我們將 y 擬合為一個高斯分布,其均值為 f(x;θ),且?guī)в袉挝粎f(xié)方差矩陣。然后我們就能最小化平均誤差:
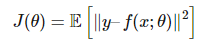
那么現(xiàn)在我們該怎樣最優(yōu)化損失函數(shù) J 以取得最優(yōu)秀的性能。首先我們要知道最優(yōu)化的困難主要有四個方面:
- 過高的數(shù)據(jù)和特征維度
- 數(shù)據(jù)集太大
- 損失函數(shù) J 是非凸函數(shù)
- 參數(shù)的數(shù)量太多(過擬合)
面對這些挑戰(zhàn),自然的方案是采用梯度下降。而對于我們的深度神經(jīng)網(wǎng)絡,比較好的方法是采用基于鏈式求導法則的反向傳播方法,該方法動態(tài)規(guī)劃地求偏導數(shù)以降誤差反向傳播以更新權(quán)重。
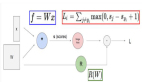
另外還有一個十分重要的技術(shù),即正則化。正則化能解決模型過擬合的問題,即通常我們對每一個特征采取一個罰項而防止模型過擬合。卷積神經(jīng)網(wǎng)絡通過參數(shù)共享提供了一個方案以解決過擬合問題。而正則化提供了另一個解決方案,我們不再最優(yōu)化 J(θ),而是最優(yōu)化 J(θ)=J(θ)+Ω(θ)。
其中Ω是「復雜度度量」。本質(zhì)上Ω對「復雜特征」或「巨量參數(shù)」引入了罰項。一些Ω正則項可以使用 L2 或 L1,也可以使用為凸函數(shù)的 L0。在深度學習中,還有其他一些方法解決過擬合問題。其一是數(shù)據(jù)增強,即利用現(xiàn)有的數(shù)據(jù)生成更多的數(shù)據(jù)。例如給定一張相片,我們可以對這張相片進行剪裁、變形和旋轉(zhuǎn)等操作生成更多的數(shù)據(jù)。另外就是噪聲,即對數(shù)據(jù)或參數(shù)添加一些噪聲而生成新的數(shù)據(jù)。
生成模型:深度玻爾茲曼機
深度學習應用了許多概率模型。我們第一個描述的是一種圖模型。圖模型是一種用加權(quán)的圖表示概率分布的模型,每條邊用概率度量結(jié)點間的相關(guān)性或因果性。因為這種深度網(wǎng)絡是在每條邊加權(quán)了概率的圖,所以我們很自然地表達為圖模型。深度玻爾茲曼機是一種聯(lián)合分布用指數(shù)函數(shù)表達的圖模型:
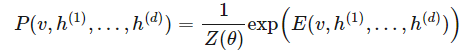
其中配置的能量 E 由以下表達式給出:
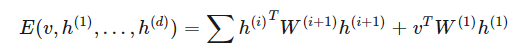
一般來說,中間層級為實數(shù)值向量,而頂部和底部層級為離散值或?qū)崝?shù)值。
波爾茲曼機的圖模型是典型的二分圖,對應于每一層的頂點只連接直接在其頂部和底部的層級。
這種馬爾可夫性質(zhì)意味著在 h1 條件下,v 分量的分布是和 h2,…,hd 還有 v 的其他分量相互獨立的。如果 v 是離散的:
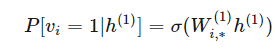
其他條件概率也是相同的道理。
不幸的是,我們并不知道如何在圖模型中抽樣或優(yōu)化,這也就極大地限制了玻爾茲曼機在深度學習中的應用。
深度信念網(wǎng)絡
深度信念網(wǎng)絡在計算上更為簡潔,盡管它的定義比較復雜。這些「混合」的網(wǎng)絡在本質(zhì)上是一個具有 d 層的有向圖模型,但是它的前兩層是無向的:P(h(d−1),h(d)) 定義為
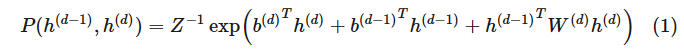
對于其它層,
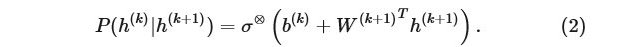
注意到這里與之前的方向相反。但是,該隱變量滿足以下條件:如果
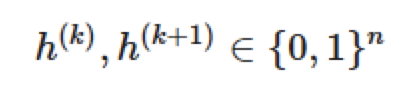
由公式(1)定義,則它們也滿足公式(2)。
我們知道怎樣通過上面的公式直接對基于其它條件層的底層進行抽樣;但是要進行推斷,我們還需要給定輸入下輸出的條件分布。
最后,我們強調(diào),盡管深度玻爾茲曼機的第 k 層取決于 k+1 層和 k-1 層,在深度信念網(wǎng)絡,如果我們只條件基于 k+1 層,我們可以準確地生成第 k 層(不需要條件基于其它層)。
課程計劃
在本課程中,我們主要的討論主題為:
- 深度的表現(xiàn)力
- 計算問題
- 簡單可分析的生成模型
第一個主題強調(diào)神經(jīng)網(wǎng)絡的表現(xiàn)力:可以被網(wǎng)絡近似的函數(shù)類型有哪些?我們計劃討論的論文有:
- Cybenko 的「迭加激活函數(shù)的近似」(89)。
- Hornik 的「多層前饋網(wǎng)絡的近似能力」(91)。
- Telgarsky 的「深度向前網(wǎng)絡的表征優(yōu)勢」(15)。
- Safran 和 Shamir 的「Relu 網(wǎng)絡的深度分離」(16)。
- Cohen、Or 和 Shashua 的「關(guān)于深度學習的表現(xiàn)力:張量分析」(15)。
前兩篇論文(我們將在后面的課程中詳細闡述)證明了「你可以僅用單一層表達任何事物」的思想。但是,后面幾篇論文表明此單一層必須非常寬,我們將在后面?zhèn)让嬲故具@種論點。
關(guān)于第二個主題,我們在本課程中討論的關(guān)于復雜度結(jié)果的內(nèi)容可能包括:
- Livni、Shalev Schwartz 和 Shamir 的「關(guān)于訓練神經(jīng)網(wǎng)絡的計算效率」(14)。
- Danieli 和 Shalev-Schwartz 的「學習 DNF 的復雜度理論限制」(16)。
- Shamir 的「特定分布的學習神經(jīng)網(wǎng)絡復雜度」(16)。
在算法方面:
- Janzamin、Sedghi 和 Anandkumar 的「使用張量方法有效訓練神經(jīng)網(wǎng)絡」(16)。
- Hardt、Recht 和 Singer 的「訓練更快,泛化更佳」(16)。
- 最后,我們將閱讀的關(guān)于生成模型的論文將包括:
- Arora 等人(2014)的「學習一些深度表征的可證明約束」。
- Mossel(2016)的「深度學習和生成層次模型」。
今天我們將開始研究關(guān)于第一個主題的前兩篇論文:Cybenko 和 Hornik 的論文。
Cybenko 和 Hornik 的理論
在 1989 年的論文中,Cybenko 證明了以下結(jié)論:
[Cybenko (89)] 令 σ 為一個連續(xù)函數(shù),且極限 limt→–∞σ(t)=0 和 limt→+∞σ(t)=1。(例如,σ 可以為激活函數(shù)且 σ(t)=1/(1+e−t))然后,f(x)=∑αjσ(wTjx+bj) 形式的函數(shù)族在 Cn([0,1]) 中是稠密的。
其中,Cn([0,1])=C([0,1]n) 是從 [0,1]n 到 [0,1] 的連續(xù)函數(shù)空間,它有 d(f,g)=sup|f(x)−g(x)|。
Hornik 證明了下面的 Cybenko 的衍生結(jié)論:
[Hornik (91)] 考慮上面定理定義的函數(shù)族,但是 σ 沒有條件限制。
如果 σ 有界且非連續(xù),那么函數(shù)族在 Lp(μ) 空間是稠密的,其中 μ 是任意在 Rk 上的有限測度。
如果 σ 是條件連續(xù)的,那么函數(shù)族在 C(X) 空間是稠密的,其中 C(X) 是所有在 X 上的連續(xù)函數(shù)的空間,X⊂Rk 是滿足有限開覆蓋的集合(compact set)。
如果附加 σ∈Cm(Rk),則函數(shù)族在 Cm(Rk) 空間和 C^{m,p}(μ)是稠密的,對于任意有限 μ 滿足有限開覆蓋條件。
如果附加 σ 至 m 階導數(shù)有界,那么對于任意在 Rk 上的有限測度 μ,函數(shù)族在 C^{m,p}(μ) 是稠密的。
在上面的理論中,Lp(μ) 空間是滿足 ∫|f|pdμ<∞ 的函數(shù) f 的空間,有 d(f,g)=(∫|f−g|pdμ)1/p。在開始證明之前,我們需要快速回顧函數(shù)分析知識。
Hahn-Banach 擴展定理
如果 V 是具有線性子空間 U 和 z∈V∖U¯ 的標準向量空間,那么會出現(xiàn)連續(xù)的線性映射 L:V→K(L(x) = 0),與 L(z) = 1(對于所有 x∈U),和 ‖L‖≤d(U,z)。
為什么此定理有用?Cybenko 和 Hornik 的結(jié)果是使用 Hahn-Banach 擴展定理反證法證明的。我們考慮由 {Σαjσ(wTjx + bj)} 給出的子空間 U,并且我們假設反證 U¯ 不是整個函數(shù)空間。我們得出結(jié)論,在我們的函數(shù)空間上存在一個連續(xù)的線性映射 L,其在 U¯ 上限制為 0,但不是恒為零。換句話說,它足以表明在 U 上為零的任何連續(xù)線性映射 L 必須是零映射,即證明了我們想要的結(jié)果。
現(xiàn)在,函數(shù)分析中的經(jīng)典結(jié)果表明,Lp(μ) 上的連續(xù)線性函數(shù) L 可以表示為
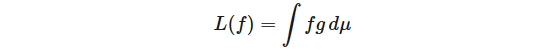
對于 g∈Lq(μ),其中 1/p + 1/q = 1。連續(xù)線性函數(shù) L 在 C(X) 上可以表示為
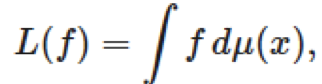
其中 μ 是 X 上的有限符號測度。
我們可以在其它空間找到與 Cybenko 和 Hornik 定理中考慮的類似的線性函數(shù)表達式。
在一般證明之前,考慮函數(shù)空間是 Lp(μ) 和 σ(x) = 1(x≥0)的(容易)的例子。如何證明,如果定理所定義的集合中的所有 f 都滿足 L(f) = 0,則與 L 相關(guān)聯(lián)的函數(shù) g∈Lq(μ) 必須恒為零?通過轉(zhuǎn)換,我們從 σ 獲得任何間隔的指標,即,可以表明對于任何 a < b,∫bagdμ= 0。由于 μ 有限(σ 有限性滿足條件),所以 g 必須為零。使用這個例子,我們現(xiàn)在考慮 Cybenko 定理的一般情況。我們想表明
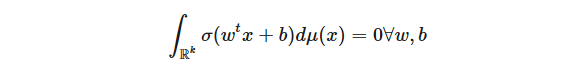
意味著 μ= 0。首先,我們使用以下傅里葉分析技巧將維度減小到 1:將測度 μa 定義為
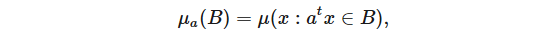
我們觀察到
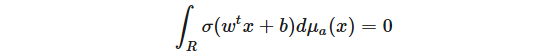
此外,如果我們可以表明,對于任意 a,μa ≡ 0,那么 μ≡0(「一個測度由它的所有投影定義」),即
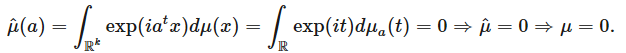 (注意,這里使用了 μ 的有限性)。將維度減少到 1 后,我們使用另一個非常有用的技巧(也使用 μ 的有限性)——卷積技巧。通過將 μ 與小高斯核進行卷積,我們得到一個具有密度的測度,即 Lebesgue 測度。我們現(xiàn)在進行剩下的證明。通過卷積技巧,我們有
(注意,這里使用了 μ 的有限性)。將維度減少到 1 后,我們使用另一個非常有用的技巧(也使用 μ 的有限性)——卷積技巧。通過將 μ 與小高斯核進行卷積,我們得到一個具有密度的測度,即 Lebesgue 測度。我們現(xiàn)在進行剩下的證明。通過卷積技巧,我們有
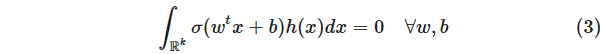
并希望證明密度 h = 0。改變變量,我們重寫條件(3)為
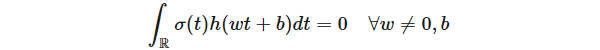
為了證明 h = 0,我們使用以下抽象傅里葉分析的工具。令 I 是所有 h(wt+b) 的擴展線性空間的閉集合。由于 I 函數(shù)的不變性,所以在卷積下是不變的;在抽象傅立葉分析中,I 是對于卷積的一個理想狀態(tài)。令 Z(I) 表示所有函數(shù)在 I 上 vanish 的傅里葉變換 ω 的全部集合;那么 Z(I) 為 R 或 {0} 集,因為如果 g(t) 處于理想狀態(tài),則對于 w≠0,g(tw) 也是處于理想狀態(tài)。如果 Z(I) = R,則在理想狀態(tài)所有函數(shù)為常數(shù) 0,即證。否則,Z(I) = {0},則通過傅里葉分析,I 為所有 f^ = 0 的函數(shù)集合;即所有非常數(shù)函數(shù)。但是如果 σ 與所有非常數(shù)函數(shù)正交,σ = 0。我們得出結(jié)論:Z(I) = R,即 h = 0,完成證明。
原文鏈接:http://elmos.scripts.mit.edu/mathofdeeplearning/2017/03/09/mathematics-of-deep-learning-lecture-1/