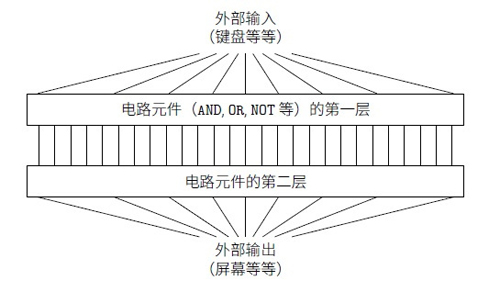
假設(shè)你是一名工程師，接到一項(xiàng)從頭開始設(shè)計(jì)計(jì)算機(jī)的任務(wù)。某天，你在工作室工作，設(shè)計(jì)邏輯電路，構(gòu)建AND門，OR門等等時(shí)，老板帶著壞消息進(jìn)來(lái)：客戶剛剛添加了一個(gè)奇特的設(shè)計(jì)需求：整個(gè)計(jì)算機(jī)的線路的深度必須只有兩層：

你驚呆了，跟老板說(shuō)道：“這貨瘋掉了吧！”

老板說(shuō)：“我也認(rèn)為他們瘋了，但是客戶的需求比天大，我們要滿足它。”

實(shí)際上，在某種程度上看，他們的客戶并沒(méi)有太瘋狂。假設(shè)你可以使用某種特殊的邏輯門，它讓你對(duì)任意多的輸入做AND運(yùn)算。同樣也能使用多輸入的NAND門——可以對(duì)多個(gè)輸入做AND運(yùn)算并取負(fù)的門。有了這類特殊的門，構(gòu)建出來(lái)的兩層深度的電路可以計(jì)算任何函數(shù)。

但是僅僅因?yàn)槟臣率抢碚撋峡赡艿模⒉淮磉@是一個(gè)好的想法。在實(shí)踐中，在解決線路設(shè)計(jì)問(wèn)題（或者大多數(shù)的其他算法問(wèn)題）時(shí)，我們通常考慮如何解決子問(wèn)題，然后逐步地集成這些子問(wèn)題的解。換句話說(shuō)，我們通過(guò)多層的抽象來(lái)獲得最終的解答。

例如，假設(shè)我們來(lái)設(shè)計(jì)一個(gè)邏輯線路來(lái)做兩個(gè)數(shù)的乘法。我們希望在已經(jīng)有了計(jì)算兩個(gè)數(shù)加法的子線路基礎(chǔ)上創(chuàng)建這個(gè)邏輯線路。計(jì)算兩個(gè)數(shù)和的子線路也是構(gòu)建在用于兩個(gè)比特相加的子子線路上的。粗略地講我們的線路看起來(lái)像這個(gè)樣子：

最終的線路包含至少三層線路的基本部分。實(shí)際上，這個(gè)線路很可能會(huì)超過(guò)三層，因?yàn)槲覀兛梢詫⒆尤蝿?wù)分解成比上述更小的單元。但是基本思想就是這樣。

因此深度線路讓這樣的設(shè)計(jì)過(guò)程變得更加簡(jiǎn)單。但是這對(duì)于設(shè)計(jì)本身幫助并不大。其實(shí)，數(shù)學(xué)證明對(duì)于某些函數(shù)設(shè)計(jì)的?常淺的線路可能需要指數(shù)級(jí)的線路單元來(lái)計(jì)算。例如，在1980 年代早期的一系列著名的論文已經(jīng)給出了計(jì)算比特的集合的奇偶性通過(guò)淺的線路來(lái)計(jì)算需要指數(shù)級(jí)的門。另一當(dāng)面，如果你使?更深的線路，那么可以使用規(guī)模很小的線路來(lái)計(jì)算奇偶性：僅僅需要計(jì)算比特的對(duì)的奇偶性，然后使用這些結(jié)果來(lái)計(jì)算比特對(duì)的對(duì)的奇偶性，以此類推，構(gòu)建出總共的奇偶性。深度線路這樣就能從本質(zhì)上獲得超過(guò)淺線路的更強(qiáng)的能力。

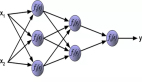
幾乎我們遇到的所有的網(wǎng)絡(luò)就只包括一層隱藏神經(jīng)元（另外還有輸入輸出層）：

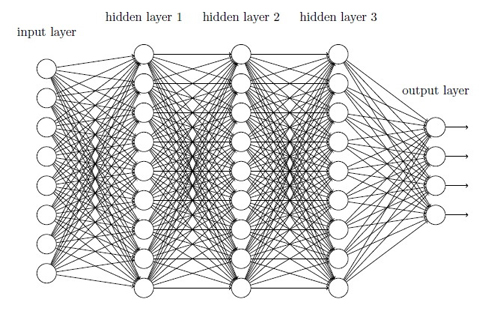
這些簡(jiǎn)單的網(wǎng)絡(luò)已經(jīng)非常有用了：在前面的章節(jié)中，我們使用這樣的網(wǎng)絡(luò)可以進(jìn)行準(zhǔn)確率高達(dá)98% 的手寫數(shù)字的識(shí)別！而且，憑直覺(jué)地看，我們期望擁有更多隱藏層的神經(jīng)網(wǎng)絡(luò)能夠變的更加強(qiáng)大：

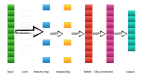
這樣的網(wǎng)絡(luò)可以使用中間層構(gòu)建出多層的抽象，正如我們?cè)诓紶柧€路中做的那樣。例如，如果我們?cè)谶M(jìn)行視覺(jué)模式識(shí)別，那么在***層的神經(jīng)元可能學(xué)會(huì)識(shí)別邊，在第二層的神經(jīng)元可以在邊的基礎(chǔ)上學(xué)會(huì)識(shí)別出更加復(fù)雜的形狀，例如三?形或者矩形。第三層將能夠識(shí)別更加復(fù)雜的形狀。以此類推。這些多層的抽象看起來(lái)能夠賦予深度網(wǎng)絡(luò)一種學(xué)習(xí)解決復(fù)雜模式識(shí)別問(wèn)題的能力。然后，正如線路的示例中看到的那樣，存在著理論上的研究結(jié)果告訴我們深度網(wǎng)絡(luò)在本質(zhì)上比淺層網(wǎng)絡(luò)更加強(qiáng)大。