論文鏈接：https://arxiv.org/abs/1706.10207

摘要：本篇論文旨在介紹關(guān)于將最優(yōu)化方法應用于機器學習的關(guān)鍵模型、算法、以及一些開放性問題。這篇論文是寫給有一定知識儲備的讀者，尤其是那些熟悉基礎優(yōu)化算法但是不了解機器學習的讀者。首先，我們推導出一個監(jiān)督學習問題的公式，并說明它是如何基于上下文和基本假設產(chǎn)生各種優(yōu)化問題。然后，我們討論這些優(yōu)化問題的一些顯著特征，重點討論 logistic 回歸和深層神經(jīng)網(wǎng)絡訓練的案例。本文的后半部分重點介紹幾種優(yōu)化算法，首先是凸 logistic 回歸，然后討論一階方法，包括了隨機梯度法（SGD）、方差縮減隨機方法（variance reducing stochastic method）和二階方法的使用。最后，我們將討論如何將這些方法應用于深層神經(jīng)網(wǎng)絡的訓練，并著重描述這些模型的復雜非凸結(jié)構(gòu)所帶來的困難。

1 引言

在過去二十年里，機器學習這一迷人的算法領(lǐng)域幾乎以史無前例的速度崛起。機器學習以統(tǒng)計學和計算機科學為基礎，以數(shù)學優(yōu)化方法為核心。事實上，近來優(yōu)化方法研究領(lǐng)域中的許多最新理論和實際進展都受到了機器學習和其它數(shù)據(jù)驅(qū)動的學科的影響。然而即使有這些聯(lián)系，統(tǒng)計學、計算機科學和致力于機器學習相關(guān)問題的優(yōu)化方法研究之間仍存在許多障礙。因此本文試圖概述機器學習學習算法而打破這種障礙。

本篇論文的目的是給出與機器學習領(lǐng)域相關(guān)的一些關(guān)鍵問題和研究問題的概述。考慮到涉及運籌學領(lǐng)域的知識，我們假設讀者熟悉基本的優(yōu)化方法理論，但是仍將引入在廣義機器學習領(lǐng)域使用的相關(guān)術(shù)語和概念，希望借此促進運籌學專家和其它貢獻領(lǐng)域的人員之間的溝通。為了實現(xiàn)這一目的，我們在詞匯表 1 中列出了本論文將介紹和使用的最重要的術(shù)語。

1.1 闡明動機
1.2 學習問題和優(yōu)化問題
1.3 學習邊界、過擬合和正則化

2 解決Logistic回歸問題的優(yōu)化方法（淺層模型的優(yōu)化方法）

當 L 和 r 是關(guān)于 w 的任意凸函數(shù)時，可以運用在本節(jié)中討論的方法來解決問題（11）：

這一類中包含很多機器學習模型，包括支持向量機、Lasso（Least Absolute Shrinkage and Selection Operator）、稀疏逆協(xié)方差選擇等。有關(guān)這些模型的詳細信息請參見 [86] 和其中的參考文獻。為了每一步都能具體（展現(xiàn)出來），此處我們指定以二分類的正則化logistic回歸為例（進行講解）。為了簡化例子中的符號，我們作不失一般性的假設，令。（此處省去了偏置項 b0），這一省略操作可以通過在輸入向量上增加一維恒為 1 的特征值來彌補）。當 w 和 x 都是 d 維時就可以令其為特定的凸優(yōu)化問題。

值得一提的是，對于此類問題，正則化項必不可少。想一想為什么說它必不可少，假設對于所有的 i ∈{1,...,n}，有參數(shù)向量 w，滿足 yi(wT*xi) > 0 以及（存在）無界射線 {θw : θ > 0}。那問題就很明朗了，在這個例子中，當 θ →∞時，

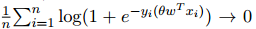
也就是說函數(shù)（式 12）無法取最小值。另一方面，通過增加（強制）正則化函數(shù) r，可以保證問題（12）將具有最優(yōu)解。

對于正則化函數(shù) r，我們將會參考常用選擇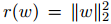和 r(w) = ||w||1。不過為了簡單起見，我們通常會選擇前者，因為它使得公式 12 對于每一個因子是連續(xù)可微的。相反，r(w) = ||w||1 會導致非平滑問題，為此，（實現(xiàn)）函數(shù)最小化就需要更復雜的算法。

2.1 一階方法

我們首先討論用一階方法求解問題（12），這里的」一階」僅僅指對函數(shù) F 中的參數(shù)進行一階偏導的數(shù)學技巧。

2.1.1 梯度下降法

從概念上講，最小化光滑凸目標的最簡單的方法是梯度下降法，具體分析參見 [ 62 ]。在這種方法中，從初始化估計值 w0 開始，通過下述公式迭代地更新權(quán)重估計值。

其中 αk > 0 是一個步長參數(shù)。步長序列 {αk} 的選擇直接決定此算法的性能。在優(yōu)化研究領(lǐng)域，人們普遍認為，在每次迭代中采用線性搜索來確定 {αk }，可以為解決各種類型的問題找到一個性能優(yōu)越的算法。然而，對于機器學習應用程序來說，這種運算成本高昂，因為每次函數(shù) F 的計算都需要傳遞整個數(shù)據(jù)集，如果 n 過大，很可能帶來高昂的（訓練）成本。

好在當每個αk 都設置為一個正的常數(shù)α且它是一個足夠小的固定值時，從理論上分析，該算法的收斂性仍可以得到保證。（固定的步長常數(shù)在機器學習領(lǐng)域叫做學習率。但即使不是常數(shù)，也有人把αK 或整個序列 {αK } 叫做學習率）。該算法的收斂速度取決于函數(shù) f 是強凸函數(shù)還是弱凸函數(shù)。

用于解決 L1 范數(shù)正則化的logistic回歸問題的梯度下降和加速梯度下降拓展算法分別被稱作 ISTA 和 FISTA。我們觀察到，在這種情況下，即使λ> 0，目標函數(shù)也不會是強凸函數(shù)。只有目標函數(shù)為凸時 [5]，ISTA 和 FISTA 具有與其對應的平滑函數(shù)相同的次線性收斂速度。

梯度下降在 ML 訓練過程中的一個重要特性就是計算出每次迭代中求解函數(shù) F 的梯度的運算成本。在 ML 的訓練過程中，單個梯度計算的成本通常是 O（ND），這個確實可以看到，例如，在正則化項為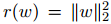的情況中，函數(shù) F 關(guān)于每一個特定的 w 的梯度是

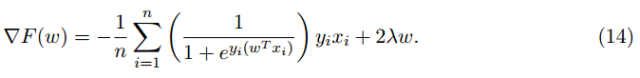
2.1.2 隨機梯度法

隨機梯度法由于其用于最小化隨機目標函數(shù)而在運籌學領(lǐng)域廣為人知，同時也是 ML 社區(qū)中的一種特征優(yōu)化算法。該算法最初由 Robbins 和 Monro [ 67 ] 在解決隨機方程組問題時提出，值得注意的是，它可以用于最小化具有良好收斂性的隨機目標，而且每次迭代的計算復雜度僅為 O（d）而不是 O（nd）（梯度下降中的計算復雜度）。

在每一次迭代中，隨機梯度法都會計算梯度 F（Wk）的無偏估計 GK。該估計可以以及低的代價計算得到；例如，對于公式（12），某次迭代的隨機梯度可被求解為

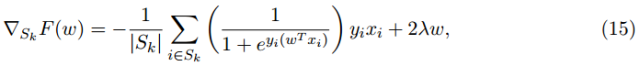
其中 Sk 被稱作小批量，它的所有元素都是從總數(shù)據(jù)集 {1,...,n} 中按均勻分布選出來的。接下來的運算類似于梯度下降：

毫無疑問，該算法的關(guān)鍵在于選擇步長序列 {αk}。不同于梯度下降，固定的步長（即學習率）不能保證算法會收斂到強凸函數(shù) F 的最小值，而只保證收斂到最小值的鄰域。

SGD 的收斂速度比梯度下降慢。尤其當函數(shù) F 是強凸函數(shù)時，該算法只保證當 k ≥ O(1/ε) 時可以得到預期精度的解（即滿足 E[F(wk)]-F(w) ≤ ε的解），而當函數(shù) F 僅僅是凸函數(shù)時，只有在 k ≥ O(1/ε^2) [11] 時才能保證得出上述解。

另一方面，正如前文提及的，如果 Sk 的大小由一個常數(shù)限定（獨立于 n 或 k 的常數(shù)），那么 SGD 的每次的迭代成本都比梯度下降法小 0（n）倍。

然而，在實際運用中，標準的 SGD 并不一定是解決機器學習中優(yōu)化問題的最有效方法。事實上，機器學習和優(yōu)化算法領(lǐng)域在開發(fā)改進或替代 SGD 方面進行了大量的積極研究。在隨后的兩部分中，我們將討論兩類方法：方差縮減法和二階方法。但是在這兩類方法以外，還有多種方法。例如，加有動量的 SGD 就是一個實踐中被發(fā)現(xiàn)的性能好于好于標準 SGD 的拓展版 SGD。見下圖算法 1

2.1.3 方差縮減法（Variance reducing method）

考慮到問題（11），人們發(fā)現(xiàn)通過利用目標 F 的結(jié)構(gòu)作為 n 個函數(shù)的有限和再加上簡單的凸函數(shù)項，可以改善 SGD 方法。目前已經(jīng)研究出幾種方法，如 SAG [74]，SAGA [22]，SDCA [76] 和 SVRG [44]。

為了方便引用，我們把 SVRG 叫做算法 2。該算法在每個外部迭代中執(zhí)行一次完整的梯度計算，然后沿著隨機方向再迭代 L 步，這是整個梯度的隨機修正過程。內(nèi)環(huán)步長 L（inner loop size）必須滿足一定的條件以保證收斂 [ 44 ]。

SVRG，全稱為隨機方差減小梯度，其名稱源自于該算法可以被視為 SGD 的方差減小變體（尤其是有限和最小化/finite-sum minimization）。

研究員通過結(jié)合 SVRG 和 SAGA 的一些思想，提出一個新的方法，叫做 SARAH。僅是內(nèi)層迭代步長不同于 SVRG，SARAH 的公式如下

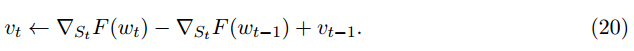
該變化導致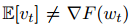 ，使得 SARAH 中的步長不基于無偏梯度估計。不過，相對于 SVRG，它獲得了改進的收斂特性。

表 2 ： 最小化強凸函數(shù)的一階方法計算復雜度

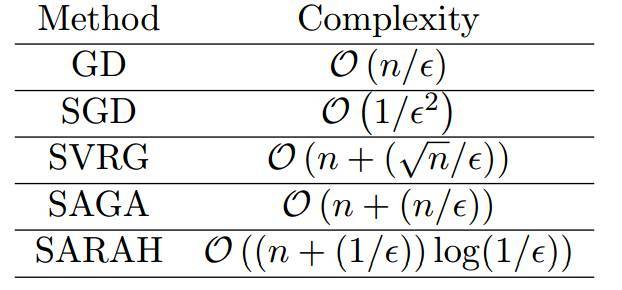
表 3 ： 最小化一般凸函數(shù)的一階方法計算復雜度

2.2 二階方法和擬牛頓法

受確定性優(yōu)化研究領(lǐng)域幾十年研究成果的激勵，ML 優(yōu)化中最活躍的研究領(lǐng)域之一就是關(guān)于如何使用二階導數(shù)（即曲率）信息來加速訓練。

不幸的是，當 n 或 d 很大時，在機器學習應用程序中，海塞矩陣（Hessian matrix）的計算和存儲變得非常昂貴。

另一類基于形如（21）模型的算法是擬牛頓方法：

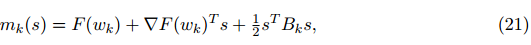
有趣的是，這些方法沒有計算出顯式二階導數(shù)，而是通過在每次迭代中應用低秩更新構(gòu)造完全由一階導數(shù)的海塞近似矩陣。例如，讓我們簡要介紹最流行的擬牛頓算法，全稱為 Broyden-Fletcher-Goldfarb-Shanno（BFGS）方法。在這種方法中，我們首先可以看到（21）的最小值為、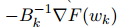進一步發(fā)現(xiàn)它實際上可以方便地計算出逆 Hessian 近似。由于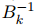隨著步長 sk = w_k+1 − wk 和位移 yk = ∇F(wk+1) − ∇F(wk) 的移動，有人選擇 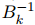以最小化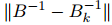以滿足割線方程 sk = (B^-1)yk。使用精心挑選的規(guī)范表達，這個問題的解析式可以顯示的寫成

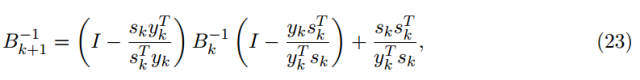
其中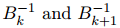之間的差異可以僅表示為二階矩陣。

為方便引用，完整的經(jīng)典 BFGS 算法被稱為算法 3。

即使采用二階信息，隨機優(yōu)化方法（無差異減少）也無法達到比次線性更快的收斂速度。不過，使用二階信息是一個不錯的想法，因為如果海塞近似矩陣收斂于海塞矩陣的真實解，則可以減少收斂速度中的常數(shù)，同時還可以減少病態(tài)（ill-conditioning）的影響。

不幸的是，盡管已經(jīng)觀察到了實際的效率提升，但在理論上還沒有一個真正的二階方法，可以實現(xiàn)這樣的提升。到目前為止，只要海塞（近似）矩陣保持良好特性，大多數(shù)實際的方法只能保證實現(xiàn) SGD 的收斂（速率）特性。例如，如果序列 {Bk}（不一定由 BFGS 更新生成）對所有 k 滿足：

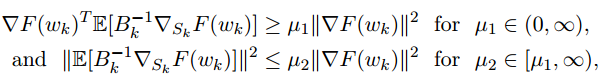
此時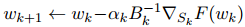具有與 SGD 相同的收斂速度屬性。我們就 可以合理地假設這些限定適用于上述討論的方法，這些假設有適當?shù)谋Ｕ稀Ｈ欢跀M牛頓方法的背景下應該小心，其中隨機梯度估計可能與海塞近似相關(guān)。

3 深度學習

沿著這些方向進行的主要進展包括深層神經(jīng)網(wǎng)絡（DNN）的運用。機器學習的一個相應的分支稱為深度學習（或分層學習），它代表了一類試圖通過使用包含連續(xù)線性和非線性變換的多層次深層圖來構(gòu)造數(shù)據(jù)中高層次抽象的算法 [6, 51, 73, 37, 38, 23]。近年來科學家們已經(jīng)研究了各種神經(jīng)網(wǎng)絡類型，包括全連接神經(jīng)網(wǎng)絡（FNN）[84,28]，卷積神經(jīng)網(wǎng)絡（CNN）[50] 和循環(huán)神經(jīng)網(wǎng)絡（RNN）[41,57,52]。對于我們來說，將主要關(guān)注前兩類神經(jīng)網(wǎng)絡，同時留意其它網(wǎng)絡。

3.1 問題公式化
3.2 隨機梯度下降法

我們引用以下內(nèi)容來強調(diào)將優(yōu)化算法應用于訓練 DNN 的令人困惑的反應。首先，例如在 [11] 中，有一個結(jié)論表明，通過應用 SGD 來最小化非凸目標函數(shù)（一直從輸入×輸出空間繪制），可以保證預期梯度風險將消失，至少在一個子序列上是這樣，即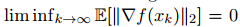：。這一結(jié)論令人欣慰，這表明 SGD 可以實現(xiàn)與其他最先進的基于梯度的優(yōu)化算法類似的收斂保證。然而，盡管文獻中的種種保證是有局限性的; 畢竟，盡管許多基于梯度的優(yōu)化算法確保目標函數(shù)單調(diào)減少，但 SG 并不以這種方式計算。因此，如果一個子序列收斂到一個固定點，那么我們怎么能確定該點不是鞍點，或者是有誤差局部最小值，亦或是一些目標值比初始點差的最大值？事實上，我們并不能肯定。也就是說，SGD 方法通常擅長找到局部極小值，而不是全局最小值。另一方面，SGD 往往會在固定值附近減緩收斂速度，這可能會阻礙它在深度神經(jīng)網(wǎng)絡中發(fā)展。

一般來說，對于非凸問題，SGD 的收斂速度記錄在 [29,30]，但是它們非常有限，特別是它們不適用于§1.3 中的討論。因此，我們不能以同樣的方式爭論 SGD 是機器學習中非凸優(yōu)化問題的最佳方法。此外，下式

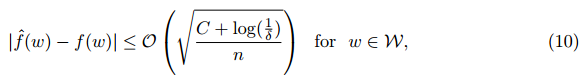
中的學習界限是沒有用的，因為對于許多 DNN 和 CNN，由神經(jīng)網(wǎng)絡產(chǎn)生的分類的復雜度 C 比訓練樣本數(shù) n 大得多。事實上，在 [90] 中，經(jīng)驗表明，只有這些集合中的數(shù)據(jù)隨機擾動，神經(jīng)網(wǎng)絡才能輕易地超過典型的數(shù)據(jù)集類型。

3.3 海塞-自由優(yōu)化方法（Hessian-free method）

有研究者發(fā)現(xiàn)我們可以修改 DNN 的反向傳播算法來計算這樣的海塞-矢量乘積，因為它們可以被看作是方向?qū)?shù) [65]。計算這種乘積的復雜度只是比計算梯度多一個常數(shù)因子。所得到的類的方法通常被稱為海塞-自由優(yōu)化方法，因為當訪問和使用 Hessian 信息時，沒有顯式地存儲 Hessian 矩陣。

由于目標函數(shù)的非凸性，在 DNN 的情況中出現(xiàn)了其它的問題，真正的海塞矩陣可能不是正定矩陣。一般來說，在確定性優(yōu)化中，處理這個問題的兩種可能的方法是修改海森矩陣和運用置信域（trust region）方法。這兩種方法都在訓練 DNN 的情況中探討過，例如，在 [54,55] 中，提出了一種高斯牛頓法，其在（11）中函數(shù) F 的 Hessian 的公式中的第一項近似于 Hessian 矩陣（省略了正則化項）

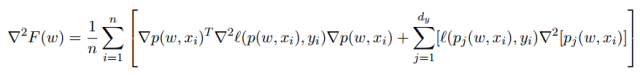
其中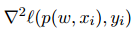是關(guān)于第一個參數(shù)的損失函數(shù) l(·, ·) 的海塞矩陣，∇p(w, xi) 是 dy-維函數(shù) p(w, x) 對于權(quán)重 w 的雅可比式，∇^2 [pj (w, xi)] for all j ∈ {1, . . . , dy} 是關(guān)于 w 的按元素運算的海塞矩陣。

3.4 子采樣海森方法（Subsampled Hessian method）

最近，在一系列論文（3, 15, 34）中，研究員們利用一個很一般的隨機模型框架，對凸區(qū)域和非凸情形下的置信域、線搜索和自適應三次正則化方法進行了分析。在這項工作中，它表明，只要梯度和 Hessian 估計是足夠準確的一些正概率，使用隨機不精確梯度和 Hessian 信息的標準優(yōu)化方法就可以保留其收斂速度。

在機器學習和采樣 Hessian 和梯度的情況下，結(jié)果只要求| SK |必須選擇足夠大的相對于該算法采取的步驟的長度。例如，在 [ 3, 34 ]，| SK |大小與置信域半徑的關(guān)系。需要注意的是，對于采樣的海塞矩陣，其對樣本集的大小要求比采樣的梯度要高得多，因此支持使用精確梯度的海塞估計的思想催生了強大的算法，它擁有強大理論支撐和良好的實踐高效性。