更細致的排序算法總結
| 排序算法 | 平均時間復雜度 |
|---|---|
| 冒泡排序 | O(n2) |
| 選擇排序 | O(n2) |
| 插入排序 | O(n2) |
| 希爾排序 | O(n1.5) |
| 快速排序 | O(N*logN) |
| 歸并排序 | O(N*logN) |
| 堆排序 | O(N*logN) |
| 基數排序 | O(d(n+r)) |
一. 冒泡排序(BubbleSort)
-
基本思想:兩個數比較大小,較大的數下沉,較小的數冒起來。
-
過程:
- 比較相鄰的兩個數據,如果第二個數小,就交換位置。
- 從后向前兩兩比較,一直到比較最前兩個數據。最終最小數被交換到起始的位置,這樣***個最小數的位置就排好了。
- 繼續重復上述過程,依次將第2.3...n-1個最小數排好位置。
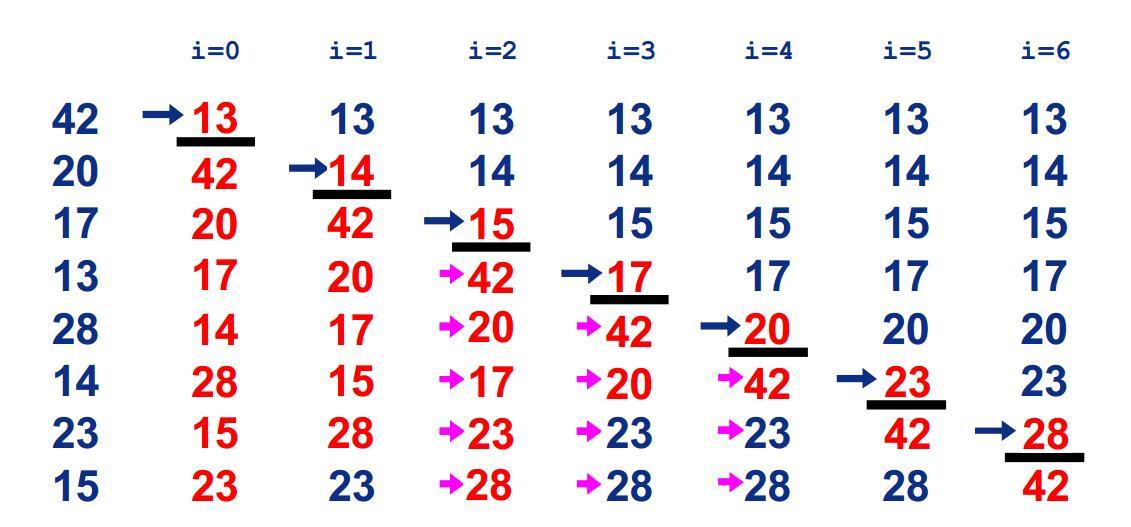 冒泡排序
冒泡排序
-
平均時間復雜度:O(n2)
-
java代碼實現:
- public static void BubbleSort(int [] arr){
- int temp;//臨時變量
- for(int i=0; i<arr.length-1; i++){ //表示趟數,一共arr.length-1次。
- for(int j=arr.length-1; j>i; j--){
- if(arr[j] < arr[j-1]){
- temp = arr[j];
- arr[j] = arr[j-1];
- arr[j-1] = temp;
- }
- }
- }
- }
-
優化:
-
針對問題:
數據的順序排好之后,冒泡算法仍然會繼續進行下一輪的比較,直到arr.length-1次,后面的比較沒有意義的。 -
方案:
設置標志位flag,如果發生了交換flag設置為true;如果沒有交換就設置為false。
這樣當一輪比較結束后如果flag仍為false,即:這一輪沒有發生交換,說明數據的順序已經排好,沒有必要繼續進行下去。- public static void BubbleSort1(int [] arr){
- int temp;//臨時變量
- boolean flag;//是否交換的標志
- for(int i=0; i<arr.length-1; i++){ //表示趟數,一共arr.length-1次。
- flag = false;
- for(int j=arr.length-1; j>i; j--){
- if(arr[j] < arr[j-1]){
- temp = arr[j];
- arr[j] = arr[j-1];
- arr[j-1] = temp;
- flag = true;
- }
- }
- if(!flag) break;
- }
- }
-
二. 選擇排序(SelctionSort)
-
基本思想:
在長度為N的無序數組中,***次遍歷n-1個數,找到最小的數值與***個元素交換;
第二次遍歷n-2個數,找到最小的數值與第二個元素交換;
。。。
第n-1次遍歷,找到最小的數值與第n-1個元素交換,排序完成。 -
過程:
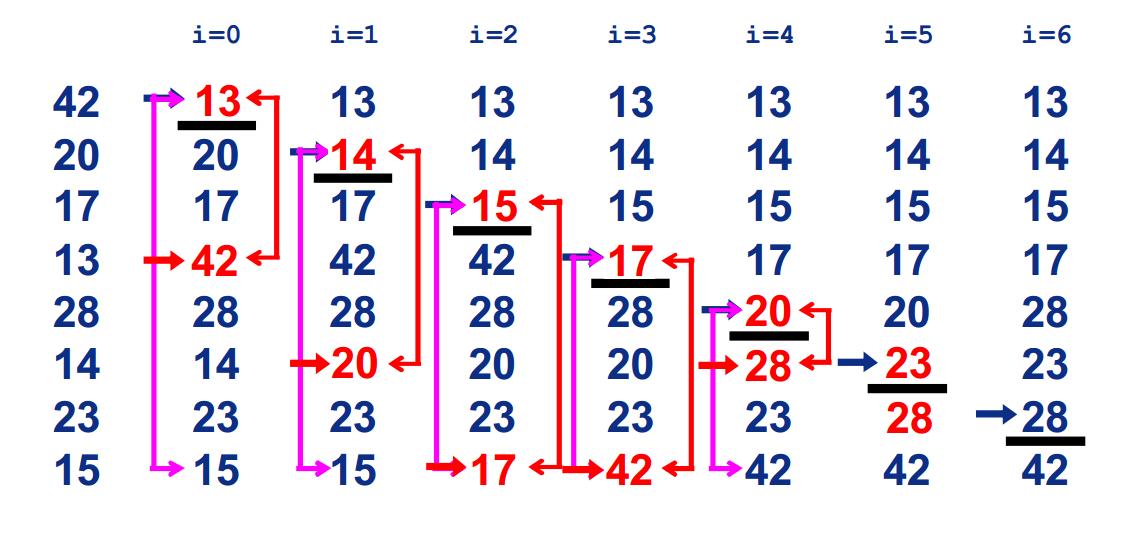 選擇排序
選擇排序 -
平均時間復雜度:O(n2)
-
java代碼實現:
- public static void select_sort(int array[],int lenth){
- for(int i=0;i<lenth-1;i++){
- int minIndex = i;
- for(int j=i+1;j<lenth;j++){
- if(array[j]<array[minIndex]){
- minIndex = j;
- }
- }
- if(minIndex != i){
- int temp = array[i];
- array[i] = array[minIndex];
- array[minIndex] = temp;
- }
- }
- }
三. 插入排序(Insertion Sort)
-
基本思想:
在要排序的一組數中,假定前n-1個數已經排好序,現在將第n個數插到前面的有序數列中,使得這n個數也是排好順序的。如此反復循環,直到全部排好順序。 -
過程:
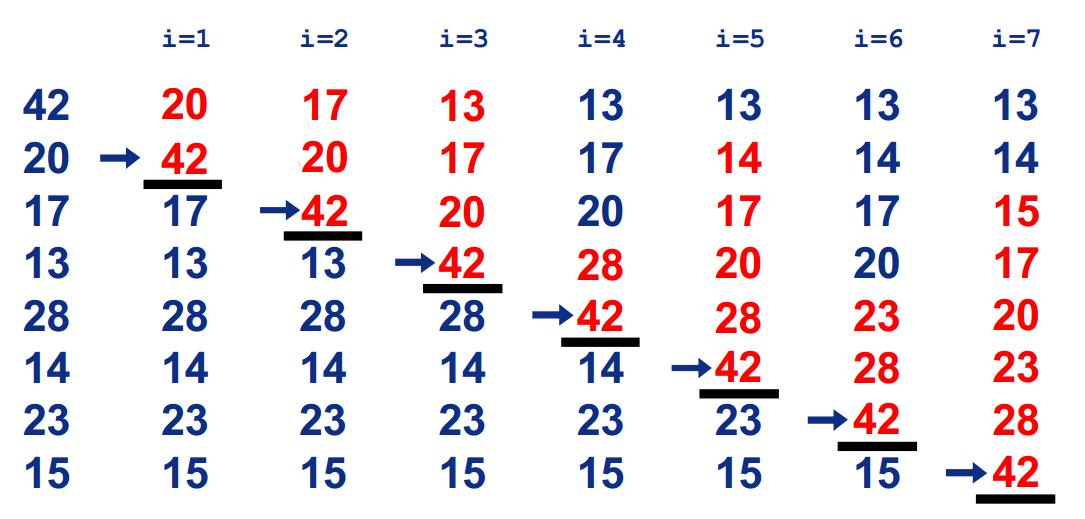 插入排序
插入排序 相同的場景
相同的場景 -
平均時間復雜度:O(n2)
-
java代碼實現:
- public static void insert_sort(int array[],int lenth){
- int temp;
- for(int i=0;i<lenth-1;i++){
- for(int j=i+1;j>0;j--){
- if(array[j] < array[j-1]){
- temp = array[j-1];
- array[j-1] = array[j];
- array[j] = temp;
- }else{ //不需要交換
- break;
- }
- }
- }
- }
四. 希爾排序(Shell Sort)
-
前言:
數據序列1: 13-17-20-42-28 利用插入排序,13-17-20-28-42. Number of swap:1;
數據序列2: 13-17-20-42-14 利用插入排序,13-14-17-20-42. Number of swap:3;
如果數據序列基本有序,使用插入排序會更加高效。 -
基本思想:
在要排序的一組數中,根據某一增量分為若干子序列,并對子序列分別進行插入排序。
然后逐漸將增量減小,并重復上述過程。直至增量為1,此時數據序列基本有序,***進行插入排序。 -
過程:
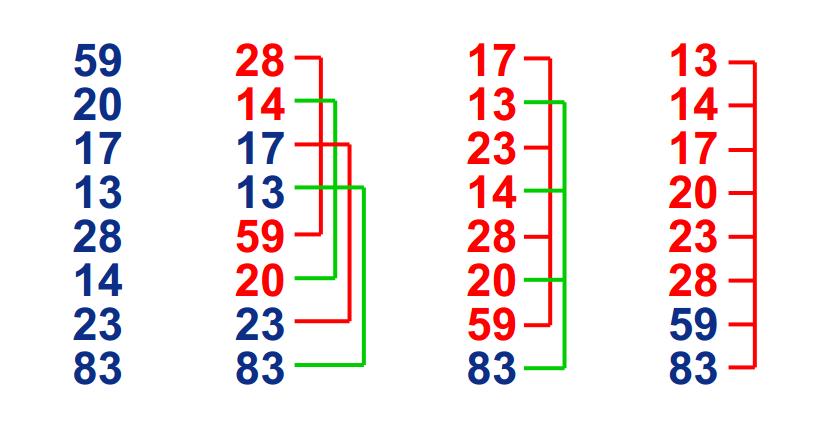 希爾排序
希爾排序 -
平均時間復雜度:
-
java代碼實現:
- public static void shell_sort(int array[],int lenth){
- int temp = 0;
- int incre = lenth;
- while(true){
- incre = incre/2;
- for(int k = 0;k<incre;k++){ //根據增量分為若干子序列
- for(int i=k+incre;i<lenth;i+=incre){
- for(int j=i;j>k;j-=incre){
- if(array[j]<array[j-incre]){
- temp = array[j-incre];
- array[j-incre] = array[j];
- array[j] = temp;
- }else{
- break;
- }
- }
- }
- }
- if(incre == 1){
- break;
- }
- }
- }
五. 快速排序(Quicksort)
-
基本思想:(分治)
- 先從數列中取出一個數作為key值;
- 將比這個數小的數全部放在它的左邊,大于或等于它的數全部放在它的右邊;
- 對左右兩個小數列重復第二步,直至各區間只有1個數。
-
輔助理解:挖坑填數
- 初始時 i = 0; j = 9; key=72
由于已經將a[0]中的數保存到key中,可以理解成在數組a[0]上挖了個坑,可以將其它數據填充到這來。
從j開始向前找一個比key小的數。當j=8,符合條件,a[0] = a[8] ; i++ ; 將a[8]挖出再填到上一個坑a[0]中。
這樣一個坑a[0]就被搞定了,但又形成了一個新坑a[8],這怎么辦了?簡單,再找數字來填a[8]這個坑。
這次從i開始向后找一個大于key的數,當i=3,符合條件,a[8] = a[3] ; j-- ;將a[3]挖出再填到上一個坑中。數組:72 - 6 - 57 - 88 - 60 - 42 - 83 - 73 - 48 - 85 0 1 2 3 4 5 6 7 8 9
- 此時 i = 3; j = 7; key=72
再重復上面的步驟,先從后向前找,再從前向后找。
從j開始向前找,當j=5,符合條件,將a[5]挖出填到上一個坑中,a[3] = a[5]; i++;
從i開始向后找,當i=5時,由于i==j退出。
此時,i = j = 5,而a[5]剛好又是上次挖的坑,因此將key填入a[5]。數組:48 - 6 - 57 - 88 - 60 - 42 - 83 - 73 - 88 - 85 0 1 2 3 4 5 6 7 8 9
- 可以看出a[5]前面的數字都小于它,a[5]后面的數字都大于它。因此再對a[0…4]和a[6…9]這二個子區間重復上述步驟就可以了。
數組:48 - 6 - 57 - 42 - 60 - 72 - 83 - 73 - 88 - 85 0 1 2 3 4 5 6 7 8 9
- 初始時 i = 0; j = 9; key=72
-
平均時間復雜度:O(N*logN)
-
代碼實現:
- public static void quickSort(int a[],int l,int r){
- if(l>=r)
- return;
- int i = l; int j = r; int key = a[l];//選擇***個數為key
- while(i<j){
- while(i<j && a[j]>=key)//從右向左找***個小于key的值
- j--;
- if(i<j){
- a[i] = a[j];
- i++;
- }
- while(i<j && a[i]<key)//從左向右找***個大于key的值
- i++;
- if(i<j){
- a[j] = a[i];
- j--;
- }
- }
- //i == j
- a[i] = key;
- quickSort(a, l, i-1);//遞歸調用
- quickSort(a, i+1, r);//遞歸調用
- }
key值的選取可以有多種形式,例如中間數或者隨機數,分別會對算法的復雜度產生不同的影響。
六. 歸并排序(Merge Sort)
-
基本思想:參考
歸并排序是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法的一個非常典型的應用。
首先考慮下如何將2個有序數列合并。這個非常簡單,只要從比較2個數列的***個數,誰小就先取誰,取了后就在對應數列中刪除這個數。然后再進行比較,如果有數列為空,那直接將另一個數列的數據依次取出即可。- //將有序數組a[]和b[]合并到c[]中
- void MemeryArray(int a[], int n, int b[], int m, int c[])
- {
- int i, j, k;
- i = j = k = 0;
- while (i < n && j < m)
- {
- if (a[i] < b[j])
- c[k++] = a[i++];
- else
- c[k++] = b[j++];
- }
- while (i < n)
- c[k++] = a[i++];
- while (j < m)
- c[k++] = b[j++];
- }
解決了上面的合并有序數列問題,再來看歸并排序,其的基本思路就是將數組分成2組A,B,如果這2組組內的數據都是有序的,那么就可以很方便的將這2組數據進行排序。如何讓這2組組內數據有序了?
可以將A,B組各自再分成2組。依次類推,當分出來的小組只有1個數據時,可以認為這個小組組內已經達到了有序,然后再合并相鄰的2個小組就可以了。這樣通過先遞歸的分解數列,再合并數列就完成了歸并排序。 - 過程:
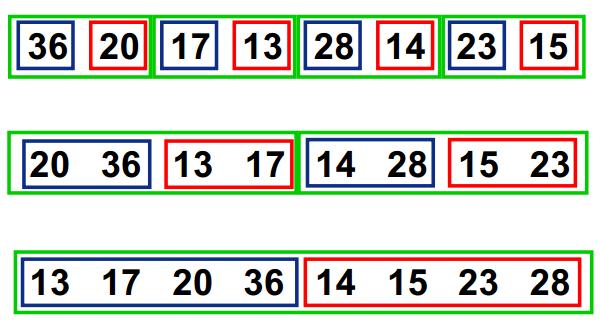 歸并排序
歸并排序 -
平均時間復雜度:O(NlogN)
歸并排序的效率是比較高的,設數列長為N,將數列分開成小數列一共要logN步,每步都是一個合并有序數列的過程,時間復雜度可以記為O(N),故一共為O(N*logN)。 -
代碼實現:
- public static void merge_sort(int a[],int first,int last,int temp[]){
- if(first < last){
- int middle = (first + last)/2;
- merge_sort(a,first,middle,temp);//左半部分排好序
- merge_sort(a,middle+1,last,temp);//右半部分排好序
- mergeArray(a,first,middle,last,temp); //合并左右部分
- }
- }
- //合并 :將兩個序列a[first-middle],a[middle+1-end]合并
- public static void mergeArray(int a[],int first,int middle,int end,int temp[]){
- int i = first;
- int m = middle;
- int j = middle+1;
- int n = end;
- int k = 0;
- while(i<=m && j<=n){
- if(a[i] <= a[j]){
- temp[k] = a[i];
- k++;
- i++;
- }else{
- temp[k] = a[j];
- k++;
- j++;
- }
- }
- while(i<=m){
- temp[k] = a[i];
- k++;
- i++;
- }
- while(j<=n){
- temp[k] = a[j];
- k++;
- j++;
- }
- for(int ii=0;ii<k;ii++){
- a[first + ii] = temp[ii];
- }
- }
七. 堆排序(HeapSort)
- 基本思想:
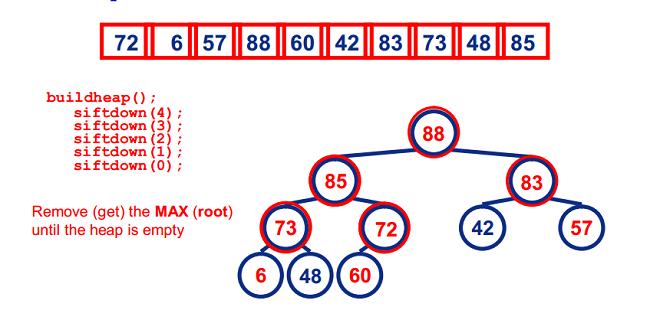
- 圖示: (88,85,83,73,72,60,57,48,42,6)
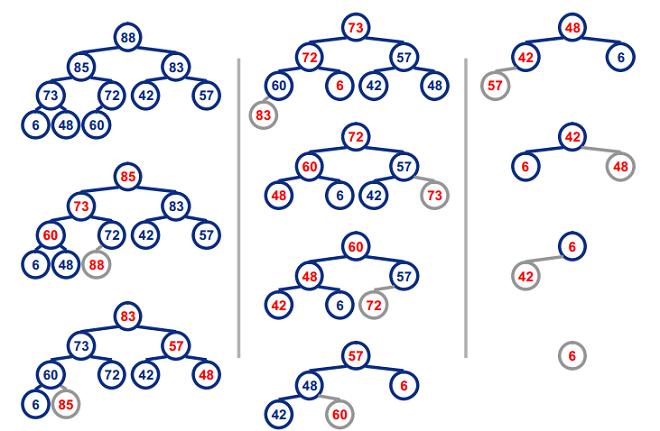 Heap Sort
Heap Sort -
平均時間復雜度:O(NlogN)
由于每次重新恢復堆的時間復雜度為O(logN),共N - 1次重新恢復堆操作,再加上前面建立堆時N / 2次向下調整,每次調整時間復雜度也為O(logN)。二次操作時間相加還是O(N * logN)。 -
java代碼實現:
- //構建最小堆
- public static void MakeMinHeap(int a[], int n){
- for(int i=(n-1)/2 ; i>=0 ; i--){
- MinHeapFixdown(a,i,n);
- }
- }
- //從i節點開始調整,n為節點總數 從0開始計算 i節點的子節點為 2*i+1, 2*i+2
- public static void MinHeapFixdown(int a[],int i,int n){
- int j = 2*i+1; //子節點
- int temp = 0;
- while(j<n){
- //在左右子節點中尋找最小的
- if(j+1<n && a[j+1]<a[j]){
- j++;
- }
- if(a[i] <= a[j])
- break;
- //較大節點下移
- temp = a[i];
- a[i] = a[j];
- a[j] = temp;
- i = j;
- j = 2*i+1;
- }
- }
- public static void MinHeap_Sort(int a[],int n){
- int temp = 0;
- MakeMinHeap(a,n);
- for(int i=n-1;i>0;i--){
- temp = a[0];
- a[0] = a[i];
- a[i] = temp;
- MinHeapFixdown(a,0,i);
- }
- }
八. 基數排序(RadixSort)
BinSort
-
基本思想:
BinSort想法非常簡單,首先創建數組A[MaxValue];然后將每個數放到相應的位置上(例如17放在下標17的數組位置);***遍歷數組,即為排序后的結果。 -
圖示:
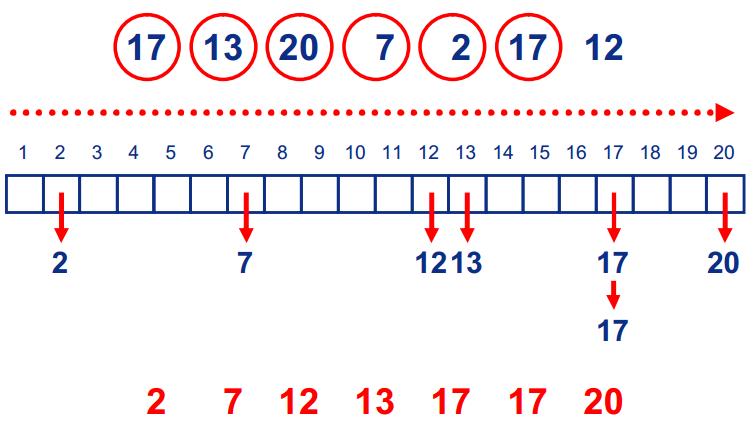 BinSort
BinSort - 問題:
當序列中存在較大值時,BinSort 的排序方法會浪費大量的空間開銷。
RadixSort
-
基本思想:
基數排序是在BinSort的基礎上,通過基數的限制來減少空間的開銷。 -
過程:
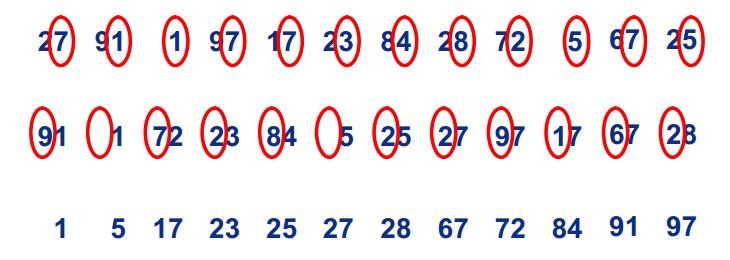 過程1
過程1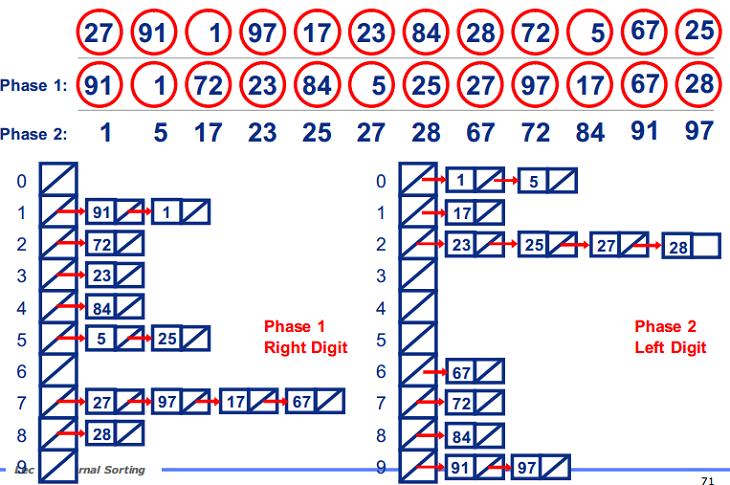 過程2
過程2
(1)首先確定基數為10,數組的長度也就是10.每個數34都會在這10個數中尋找自己的位置。
(2)不同于BinSort會直接將數34放在數組的下標34處,基數排序是將34分開為3和4,***輪排序根據最末位放在數組的下標4處,第二輪排序根據倒數第二位放在數組的下標3處,然后遍歷數組即可。 -
java代碼實現:
- public static void RadixSort(int A[],int temp[],int n,int k,int r,int cnt[]){
- //A:原數組
- //temp:臨時數組
- //n:序列的數字個數
- //k:***的位數2
- //r:基數10
- //cnt:存儲bin[i]的個數
- for(int i=0 , rtok=1; i<k ; i++ ,rtok = rtok*r){
- //初始化
- for(int j=0;j<r;j++){
- cnt[j] = 0;
- }
- //計算每個箱子的數字個數
- for(int j=0;j<n;j++){
- cnt[(A[j]/rtok)%r]++;
- }
- //cnt[j]的個數修改為前j個箱子一共有幾個數字
- for(int j=1;j<r;j++){
- cnt[j] = cnt[j-1] + cnt[j];
- }
- for(int j = n-1;j>=0;j--){ //重點理解
- cnt[(A[j]/rtok)%r]--;
- temp[cnt[(A[j]/rtok)%r]] = A[j];
- }
- for(int j=0;j<n;j++){
- A[j] = temp[j];
- }
- }
- }





























