?強化學習（RL）智能體（Agent）常常很難在現實世界中廣泛部署：初始化差異影響大，樣本效率低下，情境之外難以泛化。

研究發現問題的關鍵是違反了數據獨立同分布 (iid) 的假設，而 iid 是大多數機器學習的基礎。

強化學習（特別是具身）智能體的經驗不可避免是連續的，且跨時間點相關，這也是筆者強調的RL的非馬爾可夫性 。

昨日，Nature機器智能，發文“最大擴散強化學習（MaxDiff RL）”解決了此問題。

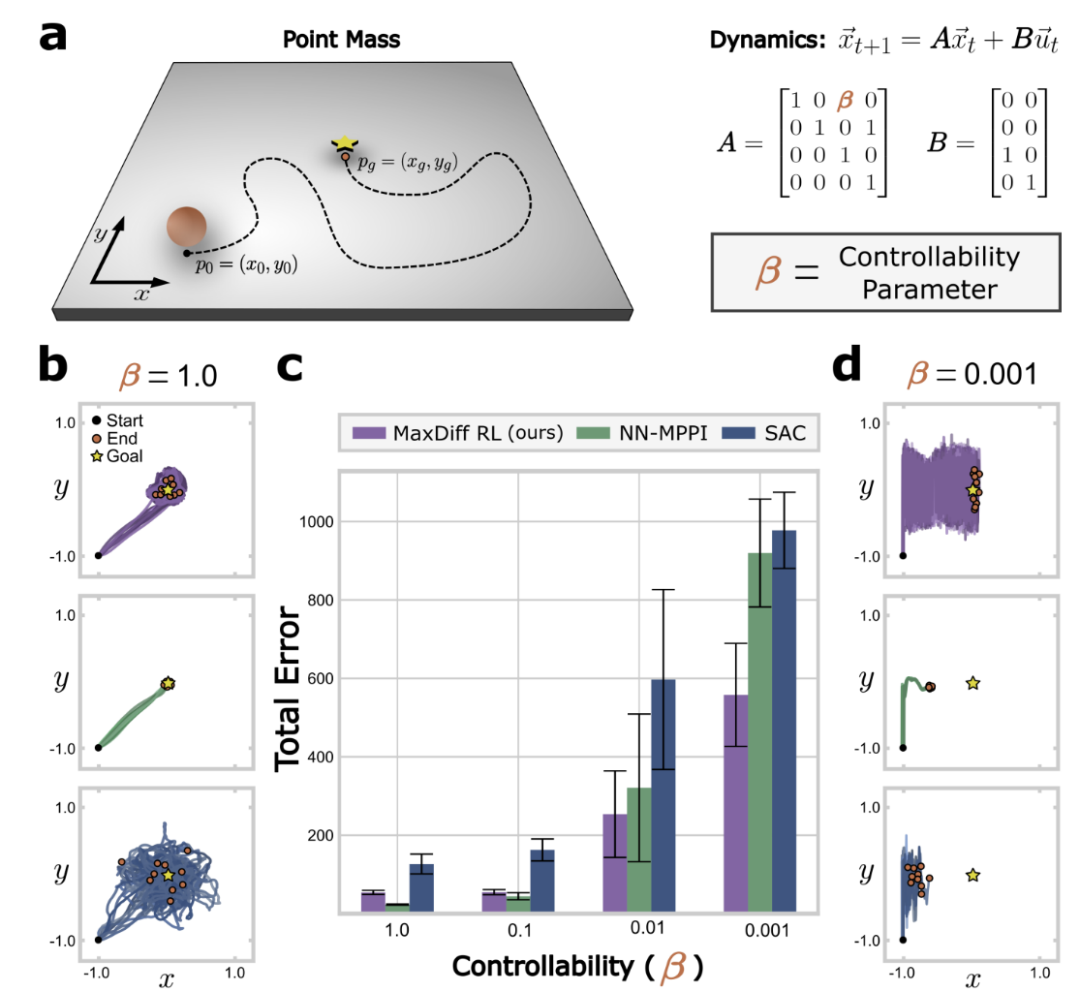
圖1：時間相關性破壞了強化學習的SOTA技術，對于大多數系統，可控屬性決定了狀態轉換之間的時間相關性。

強化學習領域的大多數方法都假設隨機行為會產生有效的探索，最大熵強化學習（MaxEnt RL）這樣的高級技術，也隱含這一假設。

不同于從固定的均勻分布或高斯分布中采樣，最大熵強化學習最大化學習到的路徑分布（即策略）的熵，以期確保足夠的隨機性來改善探索。

而實際是否可行，取決于智能體的可控屬性，與其引發的時間相關性。狀態轉換之間的時間相關性可能會阻礙有效探索，嚴重影響深度強化學習智能體的性能。 

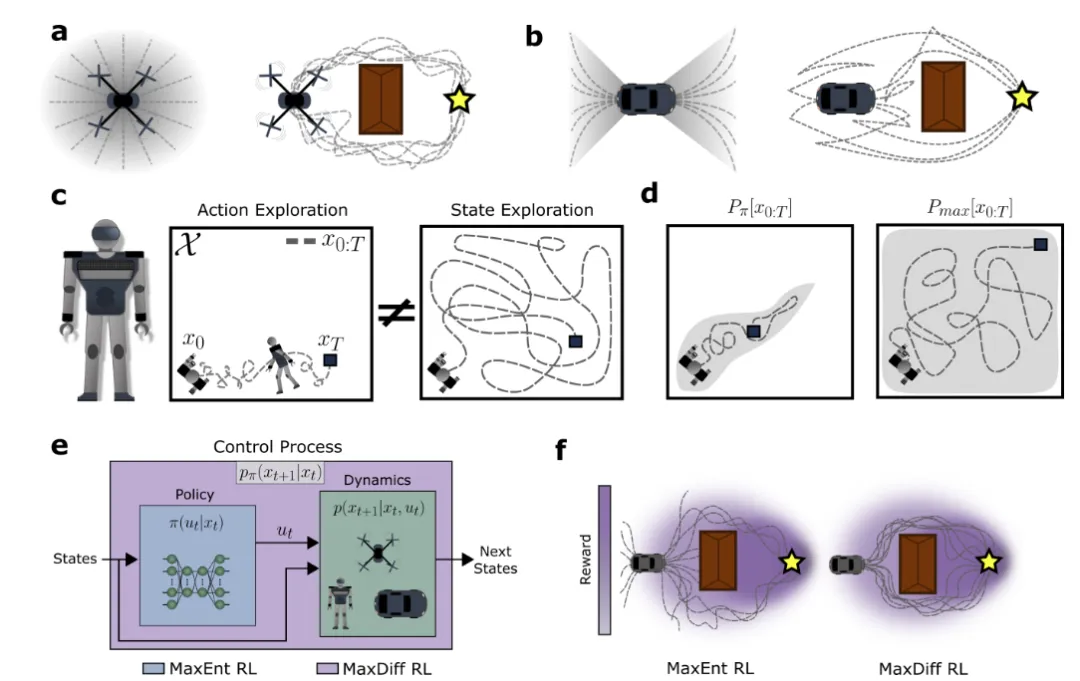
圖2：最大擴散RL緩解了時間相關性以實現有效的探索。a、b，具有不同平面可控屬性的系統。c，行動隨機化是否導致有效的狀態探索取決于基礎狀態轉移動力學的屬性。

論文從最大熵原理的統計力學中汲取靈感，該原理是最大口徑變分優化，在連續性或時間關聯約束下，優化目標是找到軌跡分布Pmax[x(t)]， 優化一個熵函數S[P[x(t)]]。

幸運的是，這個受限變分優化問題對于最大熵路徑分布具有解析解，其中Z是一個歸一化常數：

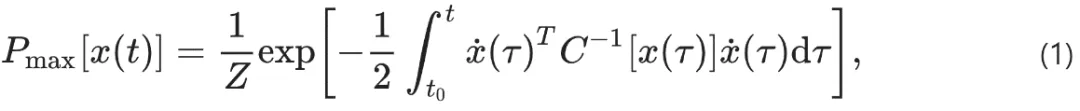
滿足遍歷性對最終智能體的性質具有深遠的影響。遍歷性是動力系統的一個正式屬性，保證了單個軌跡的統計量在漸近情況下等同于大量軌跡的統計量。

盡管強化學習智能體時間相關性使得iid采樣不可行，遍歷性強化學習智能體的全局統計量與iid采樣的統計量卻無法區分。

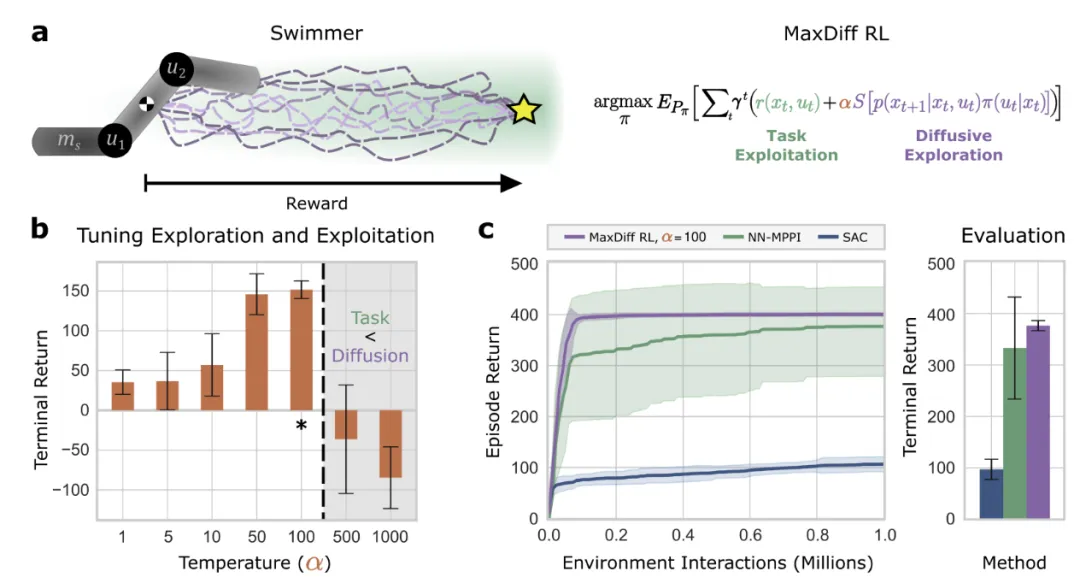
圖3：最大擴散RL智能體對隨機種子和初始化具有魯棒性。

最大擴散強化學習核心是找到一個能夠滿足最大擴散路徑統計的策略（policy）,一個policy 意味著一個軌跡分布。

找到滿足最大擴散的軌跡分布的policy，是一個優化問題：最小化“agent現在的軌跡分布與 最大擴散軌跡分布“之間的KL距離。

此KL距離可被寫成等效的隨機最優控制問題，目標是找到一種policy，最大化“智能體在環境中累計獎勵的數學期望”。α>0是超參，用于平衡擴散探索和獎勵。

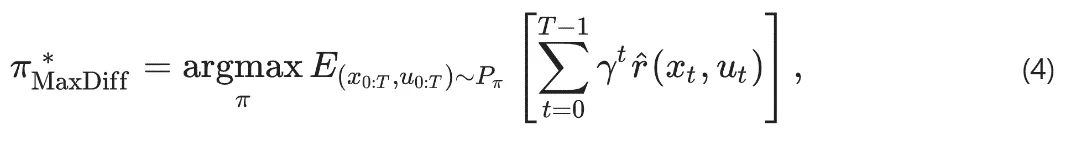
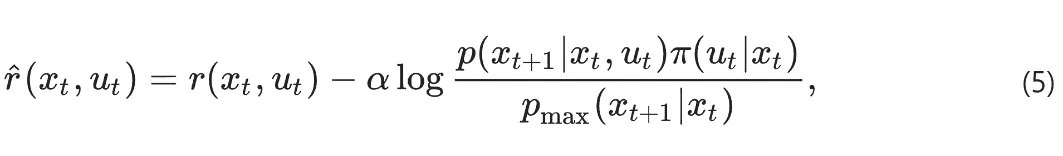
智能體路徑熵的局部估計則可以從觀察中學習到：

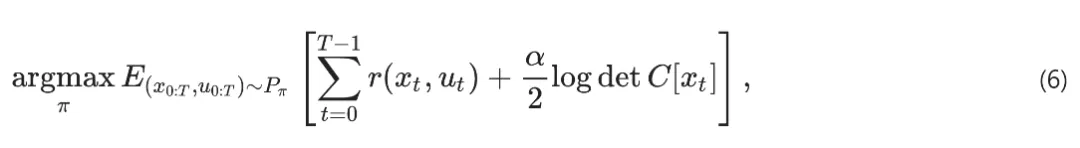
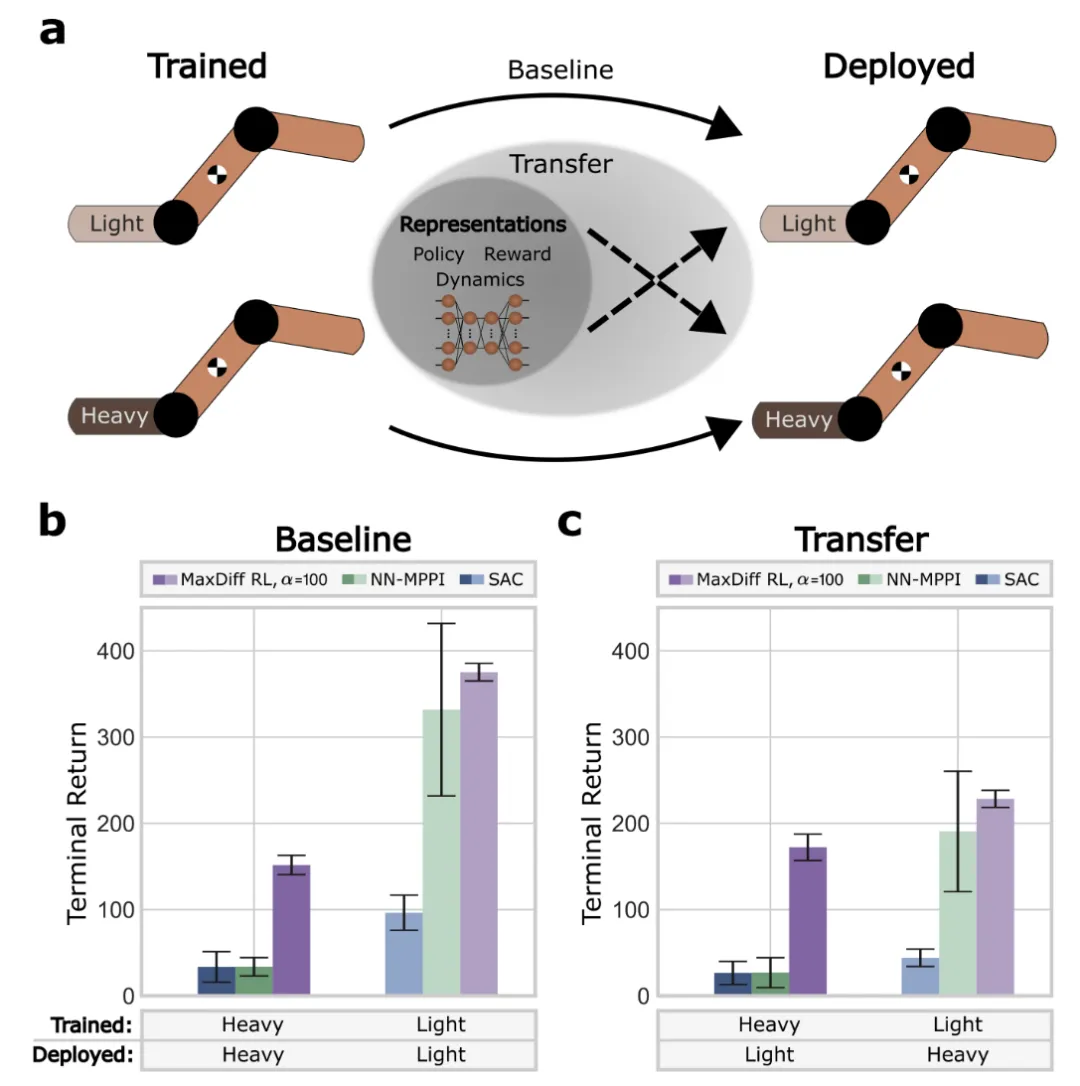
圖4：訓練系統的具身性確定了部署系統的性能。

MaxDiffRL 同時考慮策略和智能體-環境動力學的時間相關性的一般形式，若不考慮時間相關性，就褪化成MaxEntropy，即MaxEnt是MaxDiff的特例。

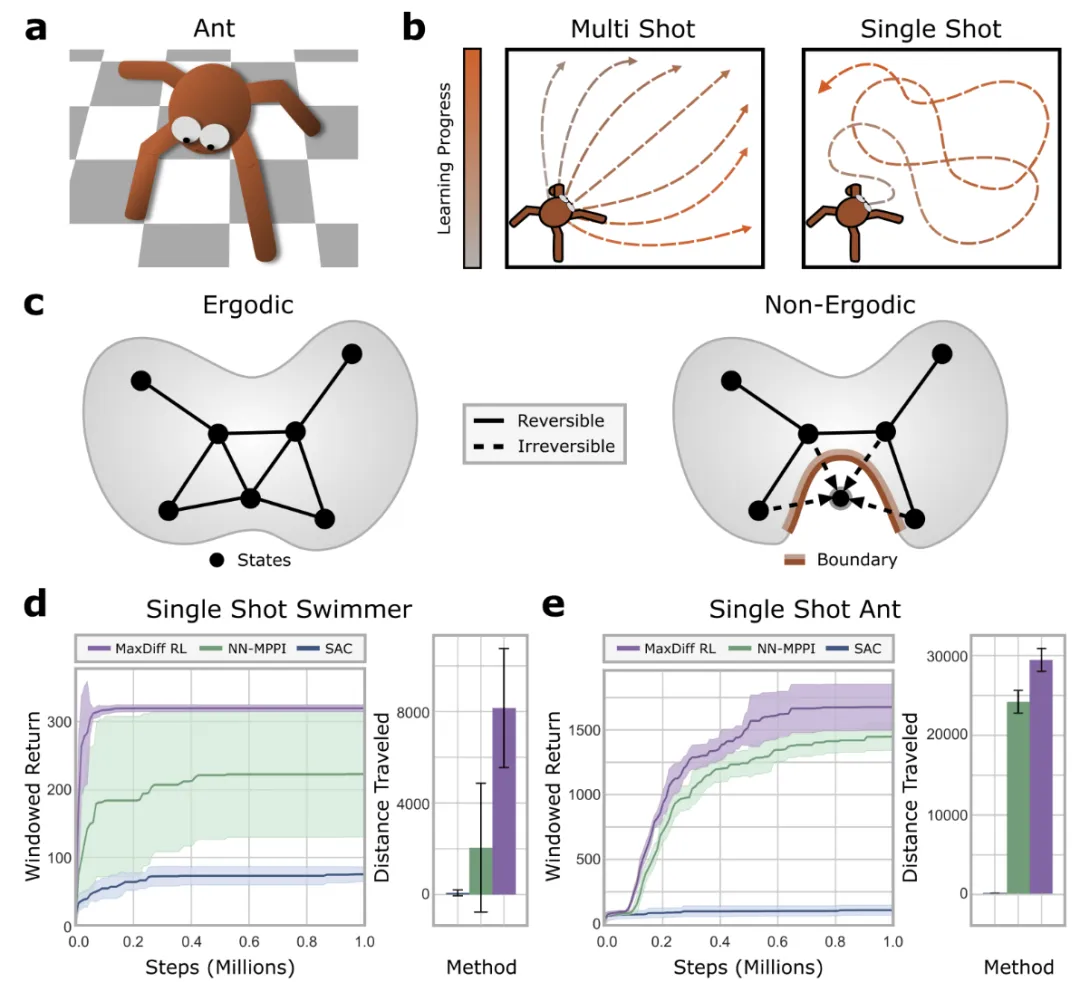
圖5：最大擴散RL智能體能夠進行單次學習。

驗證表明，MaxDiffRL方法針對初始化具有魯棒性，實現了高效單樣本學習，情境之外也易于泛化。

流行的基準測試中，MaxDiffRL也穩健地超越了SOTA。為強化學習智能體（如運動機器人和自動駕駛汽車）的更透明更可靠的決策奠定了基礎。

SORA 學習到物理原理，看起來也可以以某種方式借鑒MaxDiffRL  類似的方法，以更好的處理時空碎片狀態空間時間相關性，更好把控其動態性。

本文轉載自 ??清熙??，作者： 王慶法