“ 向量，人工智能技術的基礎結構。”

了解過人工智能技術的人應該都聽說過向量，向量可以說是人工智能的數據基礎。

那么什么是向量，為什么選擇向量呢？

什么是向量？

向量其實來源于數學，是幾何學中的一種，指的是具有大小和方向的量，一般用有向線段表示，在中學數學中向量是絕對值為1的，具有方向的量。

而用代數的方式表示向量，則是一個有序數組，包含n個元素(n在多維空間中)。

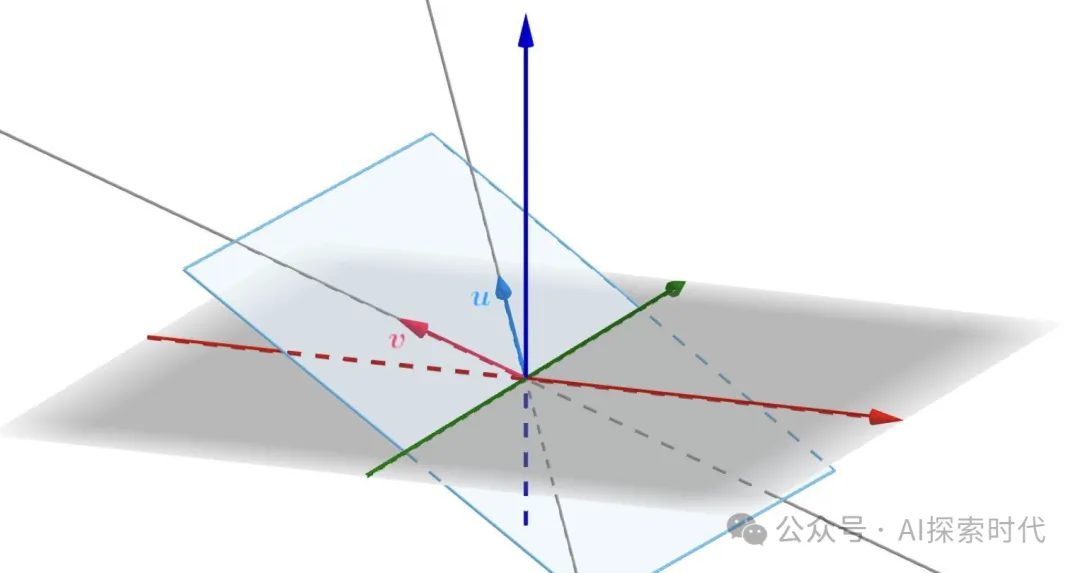
但向量并不只是數學獨有的東西，在物理學，工程學中都有使用。從數學的角度來說，向量可以進行數學運算，并且具有一定的數學性質，比如平移不變，方向唯一等。

向量有幾個特性，維數是其包含的元素數量，例如：v=[1,2,3]是一個三維向量。其次就是大小和方向，向量的大小可以通過歐幾里得范數計算；而其方向是由各分量的比率決定。

向量在人工智能領域的應用

說到人工智能，向量就是一個繞不過去的坎。

我們知道，數學是一切學科的基礎，而計算機技術也是建立在數學的理論之上，而人工智能技術作為目前計算機，數學等多學科集大成的技術，當然也離不開數學的理論基礎。

而向量就是目前人工智能領域，最基礎的數據結構。

首先，人工智能技術中數據的表示采用的是向量，比如文本——詞嵌入(Word2Vec,  GloVe)，圖片——卷積神經網絡提取圖像特征，使用向量表示，音頻——音頻信號通過傅立葉變換等方法轉化為頻譜。

其次，在機器學習等模型中，輸入與輸出采用的都是向量的格式；在大模型的訓練過程中，第一件事就是數據處理，然后轉化為向量形式，只有這樣才能被模型所處理。

再者，向量相似性計算在推薦系統，信息檢索等領域被廣泛應用，比如常見的向量數據庫。

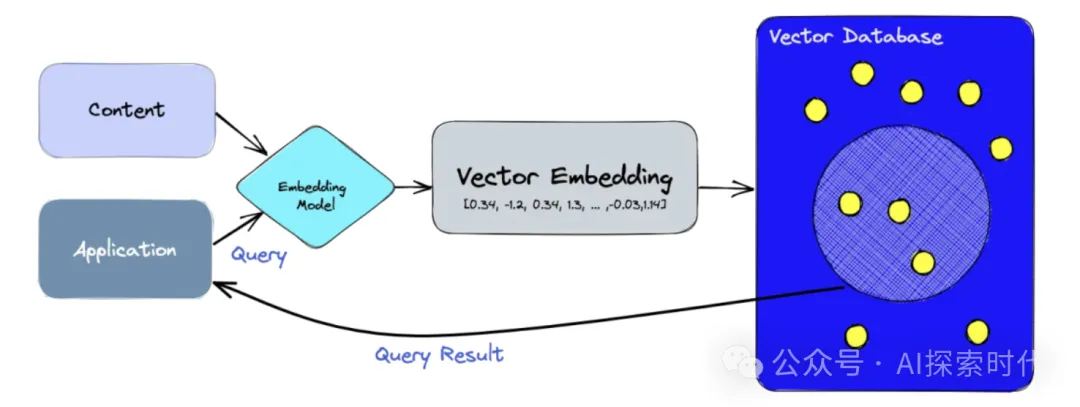
向量數據庫是一種能夠進行語義查詢等數據庫，而不是普通的關系型數據庫只能進行字符匹配，包括精確匹配和模糊匹配。

而具體的計算方式，如余弦相似度，歐式距離，曼哈頓距離等都是采用的向量形式。

在人工智能領域中，對高緯向量進行降維計算，以及神經網絡模型中，隱藏層的數據處理都離不開向量(張量)計算。

向量是人工智能中基本且重要的數據表示形式。它在數據表示、模型輸入輸出、相似性計算、特征提取等方面有廣泛應用，支持了人工智能技術的發展和應用。通過向量化操作，復雜的數據處理和分析變得更加高效和統一。

雖然說，在現有的人工智能理論中，并不能完全明白為什么大規模的參數通過向量運算可以得到近似“智能”的結果，但這并不耽誤人工智能技術的演化過程。

本文轉載自公眾號AI探索時代 作者：DFires

原文鏈接：??https://mp.weixin.qq.com/s/Jyf1gEVVgxEmMwk4j5yRYw??