近日，階躍星辰研究團隊通過大規模實證探索，耗費了近 100 萬 NVIDIA H800 GPU 小時（約百萬美元），從頭訓練了 3,700 個不同規模，共計訓了 100 萬億個 token，揭示了 LLM 超參數優化的全新的普適性縮放規律，為更好地提升 LLM 性能，提供了開箱即用的工具。該研究也是第一個全面研究模型最優超參隨著 Model Shape、Dense/MoE、預訓練數據分布的變化，是否穩定不變的工作。研究中凸顯出 Step Law 的魯棒性，大大增加了該工具的實用性和普適性。同時該團隊正在逐步開源相關資料，包括模型、訓練日志等，期待更多相關領域的人基于海量的實驗結果作出更加深入的研究與解釋。

• 論文標題：Predictable Scale: Part Ⅰ — Optimal Hyperparameter Scaling Law in Large Language Model Pretraining
• 論文鏈接：https://arxiv.org/abs/2503.04715
• 工具鏈接：https://step-law.github.io/
• 開源地址：https://github.com/step-law/steplaw
• 訓練過程：https://wandb.ai/billzid/predictable-scale

海量實驗，實證為王

研究團隊從頭訓練了 3,700 個不同規模、不同超參數組合、不同形狀、不同數據配比、不同稀疏度 (含 MoE、Dense) 的大語言模型（LLM），共訓練了超 100 萬億個 token，對超參數進行了全面的網格搜索，研究團隊發現了一條普適的縮放法則 (簡稱 Step Law)：最優學習率隨模型參數規模與數據規模呈冪律變化，而最優批量大小主要與數據規模相關。

圖一：在 400M 的 Dense LLM 上訓練 40B Token（左）和在 1B 的 Dense LLM 上訓練 100B Token（右）的超參 - 損失等高線圖，并且對業內不同方法進行比較，所有方法都轉換成了預測 Optimal Token Wise BatchSize。這里所有的等高線都是從頭訓練的小模型所得的真實收斂后的 Train Smooth Loss。左右兩張圖的所有等高線，分別來自于兩組共 240 個采用不同超參（Grid Search）的端到端訓練的小模型。Global Mimimum 是來 120 個小模型中最終 Train Smooth Loss 最小的那個。等高線表示距離 Global Mimimum 的從最終 loss 角度的相對距離。而超越 + 2% 的點位，并沒有體現在圖中。

值得關注的是，實驗表明，在固定模型大小與數據規模時，超參數優化的 Landscape 呈現出明顯的凸性特征，這意味著存在一個穩定且易尋的最優超參數區域。

圖二：Learning Rate 與 Batch Size 在 1B 模型訓練 100BToken 上的損失分布：散點圖（左）與 3D 曲面（右）圖中的每一個實心點都是真實值，是 120 個從頭訓練的一個小模型，在訓練結束之后的收斂 Loss。為了展示這樣的凸性，研究員們構造了如右圖一樣的 3 維空間，空間的橫軸為 Learning Rate，縱軸為 Batch-size，高度軸為 Loss。對于這個三維空間我們進行橫面和豎面的切割，如左上圖得到固定不同的 Learning Rate 情況下，最終收斂的 Train Smoothed Loss 隨著 Batchsize 的變化。而左下圖是固定不同的 Batchsize 情況下，最終收斂的 Train Smoothed Loss 隨著 Learning Rate 的變化。可以顯著的觀測到一種凸性，且在凸性的底端，是一個相對平坦的區域。這意味著 Optimal Learning Rate 和 Batchsize 很可能是一個比較大區域。

為了便于學界和業界應用，團隊推出了一款通用的最優超參數估算工具（https://step-law.github.io），其預測結果與窮舉搜索的全局最優超參數相比，性能僅有 0.09% 的差距。同時，研究團隊還在該網站上公開了所有超參數組合的 loss 熱力圖，以進一步推動相關研究。

圖三：1B 模型、100BToken 訓練上的 LR 與 BS 熱力圖。每一個點上的數字都是從頭訓練的一個小模型（共訓練了 120 個小模型），在訓練結束之后的收斂真實 Train Smoothed Loss。紅點是上述公式的預估值所對應的 BS、LR 位置。其中空白的部分，是因為種種原因訓練失敗的點位。所有熱力圖見https://step-law.github.io/

研究亮點：Step Law 的普適性，從三個不同角度

相較于現有的大模型最優超參數估算公式，團隊的研究進行了極其充分的、覆蓋模型參數規模（N）、訓練數據規模（D）、批量大小（BS）和學習率（LR）的網格搜索，最終得到的 Step Law 則展現出顯著的優越性，在適用性和準確度方面均有大幅提升。

表一：不同方法的最佳超參數縮放定律比較，其中 Data Recipe 是指是否有在不同的預訓練語料的配比下的最優超參進行研究。Model Sparsity 是指是否同時支持 MoE Model 和 Dense Model，以及不同的稀疏度下的 MoE 模型。LR 指的是 learning Schedule 中的峰值 Learning Rate，其中 BS 值得是 Token Wise 的 Batch Size。

角度一：跨模型形狀 (Model Shape) 的穩定性

研究還深入探討了不同模型形狀（如寬度與深度的不同組合）對縮放規律的影響，發現無論模型是以寬度為主還是深度為主，抑或是寬深平衡的設計，Step Law 均表現出了高度的穩定性。這表明，縮放規律不僅適用于特定類型的模型結構，在更廣泛的架構設計空間中依然適用，為復雜模型架構的設計和優化提供了指導意義。

圖四：最優超參在不同 Model Shape 下的拓撲不變性。這里的是固定了模型的非詞表參數量的大小，且固定了模型的訓練 Token 數，但研究團隊使用了不同的 Model Shape。例如變換了層數，從左到右分別是 14/10/8 層；變換了 Model Hidden Dimension，分別包括 1280/1536/2048 這三種；同時變換了 6 種不同的 FFN 倍數 (FFN_media_dim/model_dim)，從 1.1 倍到～6.25 倍。其中紅色五角星的點是 Step Law 預測的點位，可以觀察到 Step_law 在 6 個不同的 Shape 上都預測到了 Global Minimum 附近。然而也可以同時觀察到，不同的 Model Shape，Bottom 的一片區域的位置是會發生 shift 的。

角度二：跨模型架構的泛化性

研究結果發現，這一縮放規律不僅適用于 Dense 模型，還能很好地推廣到不同稀疏度的 MoE 模型（Mixture-of-Experts），展示了極強的泛化能力。

圖五：不同稀疏比下 MoE 模型的超參 - 損失等高線圖。左：低稀疏度（N_a/N=0.27），中間：中等稀疏度（N_a/N=0.58，D/N=10），右：中等稀疏度、較少訓練 Token 數（N_a/N=0.58，D/N=4）。研究員們在不同稀疏度，不同 D/N 的 MoE 模型配置，每一種配置都從頭訓練了 45 個小模型，來做最優超參搜取。共計從頭訓練了 495 個不同稀疏度、不同超參、不同 D/N 的 MoE 模型。從而得到了不同配置下的基于真實值的 Global Minimum Train Smoothed Loss。其中除了一組 D/N=1 的實驗，其余實驗 Step Law 預測位置都在 Global Minimum+0.5% 的范圍之內。并且大多數配置下都在 Global Minimum+0.25% 的范圍之內。充分的驗證了 Step Law 的魯棒性。詳細結果可以參考論文的附錄部分。

角度三：跨數據分布的穩定性

那么 Step Law 是否能兼容不同的預訓練數據分布呢？研究團隊進一步驗證了不同數據分布下的規律一致性：無論是英語主導、中英雙語、Code 和英語混合，還是代碼主導的數據分布，Step Law 都表現出了穩定的性能。這為多語言、多任務場景下的實際應用提供了可靠支持。

表二：實驗的不同數據分布。其中 Baseline 是得出 Step Law 的訓練 Recipe。而 Code-Math，是壓縮英文 web-data 的配比近一半，擴大 code-math 的比例至近 40%。而 More Code-Math 比例更加極端，將英文 web-data 的配比壓縮為之前的 1/4，將 Code-math 擴大為近 2/3。EN-CN 是下調英文 web-data 的配比近一半，將余量的部分都轉化為中文網頁數據。

圖六：不同數據分布下的超參 - 損失等高線。左：雙語數據（表格中 En-CN），中間：加入 Code 數據（表格中的 Code+Math），右：主要為 Code 數據（表格中的 More Code+Math）。每一個圖都是從頭訓練了 45 個模型，每一個模型除了 Bs/lr 不同以外，其他設置完全相同。總共訓練了 135 個在三種數據分布下的模型。其中 Global Minimum 是通過這種 grid search 的方法得到的最低 Final Train Smoothed Loss 的真實值。Step Law 預測出來的最優 Batch Size/Learning Rate 都在最低 Loss +0.125%/0.25% 的范圍內。

 研究細節解讀

1. 學習率調度策略優化

圖七：不同學習率策略的比較。藍色等高線 (傳統衰減策略): 學習率會從一個最大值 (max_lr) 逐漸減小到一個最小值 (min_lr，常是峰值的十分之一)。紅色等高線 (固定最終學習率策略): 保持一個固定的最小學習率 (min_lr = 1e-5)，而不是像傳統方法那樣與最大學習率掛鉤。兩張圖都分別為 120 個從頭訓練的模型，在相同的 batch size/learning rate 范圍內做的 Grid Search。紅色和藍線的 Global Minimum 都是各自配置下的真值 - 最小的 Final Train Smoothed Loss。可以觀察到改成 max_lr/10 之后，藍點會向左上方偏移，即更小的 Learning Rate 和更大的 Batchsize。如果不是對比相對值，而是對比真值，min_lr=1e-5 的最終收斂 loss 普遍小于 max_lr/10。相關的真值將陸續開源。相關的真值開源在https://github.com/step-law/steplaw

研究團隊通過對比分析發現，學習率調度策略對最優超參選擇產生顯著影響。研究揭示了傳統學習率衰減與固定最小學習率方案間的重要差異：

傳統學習率衰減方案將最小學習率設為最大值的十分之一 (max_lr/10)，而團隊提出的固定方案則采用恒定的絕對最小值 (1e-5)。等高線圖分析清晰表明，傳統衰減方法使得最優學習率區域出現明顯的左偏分布 —— 即損失最小區域向較低學習率區間顯著偏移。

團隊通過分析了傳統學習率（min_lr=max_lr/10）調度方案的局限性：采用較高初始峰值學習率時，其退火機制會同步抬升最低學習率閾值。這種耦合設計在訓練末期會使學習率超出理想區間，過大的參數更新幅度引發損失函數在收斂階段持續振蕩。相比之下，固定最小學習率策略通過解耦初始學習率與終值學習率的關聯，在訓練后期始終維持符合梯度下降動態特性的更新步長。

此外，這種固定最終較小最終學習率的策略也與業界的訓練經驗相匹配，更有實際應用價值。

2. 訓練損失與驗證損失的最優超參一致性

圖八：平滑訓練損失（Final Train Smoothed Loss）的超參 - 損失等高線圖（左）和驗證損失（Validation Loss of Final Checkpoint）的超參 - 損失等高線圖（右）。兩張圖都是在同一組實驗下進行，對于相同的模型尺寸，相同的訓練 Token 數，分別采用了 64 組不同的超參進行 Grid Search。從而得到 64 個模型的 Final Train Smoothed Loss、和 Validation Loss。

在 429M 模型上訓練 40B 的 Token 進行驗證，當平滑訓練損失達到最優時，學習率為 1.95×10^-3，批量大小為 393,216，這一點與驗證損失最優時的超參數完全重合。此外，學習率和批量大小的變化趨勢在平滑訓練損失和驗證損失中表現出高度一致性。這一發現表明，平滑的訓練損失曲線可以為實際超參數選擇提供可靠的指導。盡管采用 Train Smoothed Loss 可以降低實驗成本（節省了 Final Checkpoint 在 Validation Set 上推理的算力），但仍然具有一定的局限性，例如訓練數據不能重復。研究團隊將會陸續開源這近 4000 個模型的 Final Checkpoint，供廣大研究員進行進一步的分析。

最優超參的 Scaling Law 擬合

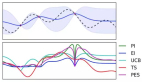
圖九：(a) 散點圖表示模型規模為 N 時，經驗最優學習率與批量大小的關系；(b) 散點圖表示數據集規模為 D 時，經驗最優學習率與批量大小的關系。曲線表示超參數縮放定律的預測結果，陰影區域表示基于采樣擬合策略得到參數不確定性范圍。圖上的每一個點，背后都代表著 45~120 個采用了不同的超參的從頭訓練的模型。圖上的每一個點位都在不同的 Model Size、Data Size 下通過 Grid Search 得到的最優的超參 (Optimal Learning Rate，Optimal Batch Size)。這張圖總共涉及了 1912 個從頭訓練的 LLM。擬合方法開源在https://github.com/step-law/steplaw

通過從頭訓練了 1912 個 LLM，研究團隊分析發現：

• 最優學習率：隨模型規模增大而減小，隨數據規模增大而增大。
• 最優批量大小：隨數據規模增大而增大，與模型規模弱相關。

研究通過對數變換將冪律關系轉化為線性形式，采用最小二乘法擬合參數，并通過 Bootstrap 采樣方法提升穩健性。最終，團隊提出了一套精確的預測公式，為大模型預訓練的超參數設置提供了一個開箱即用的工具。據了解，在階躍星辰真正的研發過程中，他們已經廣泛使用了 Step Law，主要是在大于 1B 的模型和非極端的 D/N 下適用。

討論與未來工作

研究團隊坦言，盡管付出了很多的算力，和大量的精力來分析相關的實驗。但是很多子 Topic 分析仍然是值得深究的。研究團隊認為他們的這份工作僅僅是一個開始，他們會陸續將實驗的各個細節整理并且開源出來，供整個社區的研究人員進行進一步分析和深入的理論解釋。這些子 Topic 包括以下話題：

• 在給定模型、訓練 Token 數的情況下，(Loss,bs,lr) 這三維空間是否是真正的凸性。
• 是否有更好的 optimal BS LR 的擬合方法，并且可以兼容 BS、LR 的內在關系。
• 盡管 Step Law 在不同 Model Shape、不同稀疏的 MoE 模型是魯棒的，但是次優的區域是在不同配置下是變化的，有無更好的解釋方法。
• 上文中這些基于海量 Grid Search 的數據驅動的結論的理論解釋。
• 不同的超參、不同 Model Size、Model Shape、Model Sparsity 下的 Training Dynamic 研究。

為此研究團隊公開了他們的開源計劃，以及 Predictable Scale 系列工作的發布節奏。據了解，Predictable Scale 系列后續可能進一步討論超大模型性能預測、Code&Math Scaling 性質、不同 Attention 類型的 Scaling 性質等問題。非常值得期待。